
- •Раздел III. Теория вероятностей и математическая статискика Лекция 17. Основные понятия теории вероятностей
- •17.1. Введение. Предмет теории вероятностей
- •17.2. Краткий исторический очерк
- •17.3. Случайное событие. Его частота
- •17. 4. Классическое определение вероятности. Непосредственный подсчет вероятностей.
- •Лекция 18. Алгебра событий. Основные теоремы теории вероятностей
- •18.1. Алгебра событий
- •18.2. Теорема сложения вероятностей
- •18.3. Полная группа событий. Противоположные события
- •18.4. Теорема умножения вероятностей Независимые и зависимые события.
- •18.5. Теорема умножения вероятностей независимых событий
- •18.6. Условная вероятность
- •18.7. Теорема умножения вероятностей зависимых событий
- •Лекция 19. Основные теоремы теории вероятностей (продолжение)
- •19.1. Теорема сложения вероятностей совместных событий
- •19. 2. Формула полной вероятности
- •19.3. Формулы Бейеса (формулы переоценки вероятностей гипотез)
- •19. 4. Повторение испытаний. Формула Бернулли
- •Лекция 20. Случайные величины и их законы распределения
- •20.1. Дискретные и непрерывные случайные величины
- •Понятие закона распределения вероятностей дискретной случайной величины
- •20. 3. Биноминальное распределение
- •20. 4. Распределение Пуассона
- •20. 5. Простейший пуассоновский поток событий
- •21.2. Математическое ожидание и его основные свойства
- •21.3. Дисперсия дискретной случайной величины
- •21.4. Среднее квадратическое отклонение
- •21.5. Свойства дисперсии
- •21. 6. Понятие о моментах распределения
- •21.7. Определение интегральной функции распределения
- •21.8. Свойство интегральной функции
- •21.9. График интегральной функции
- •22.2. Вероятность попадания непрерывной случайной
- •22.3. Нахождение интегральной функции распределения по известной дифференциальной
- •22.4. Свойства дифференциальной функции. Ее вероятностный смысл
- •22.5. Математическое ожидание. Дисперсия. Среднее квадратическое отклонение
- •22.6. Начальные и центральные моменты
- •22.7. Коэффициент асимметрии
- •22.8. Эксцесс
- •22.9. Мода. Медиана
- •Лекция 23. Законы распределения непрерывной случайной величины
- •Закон равномерного распределения или закон равномерной плотности
- •23.2. Нормальное распределение
- •23.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на интервал [
- •23.4. Правило трех сигм
- •Лекция 24. Система случайных величин
- •24.1. Понятие о системе случайных величин
- •24.2. Закон распределения вероятностей дискретной двумерной случайной величины
- •24.3. Интегральная и дифференциальная функция распределения двумерной случайной величины и их свойства
- •24.4. Условные законы распределения составляющих системы дискретных случайных величин
- •24.5. Числовые характеристики системы двух случайных величин
- •24.6. Коррелированность и зависимость случайных величин
- •Лекция 25. Предельные теоремы
- •25.1. Закон больших чисел
- •25.2. Теорема Чебышева
- •25.3. Теорема Бернулли
- •25.4. Центральная предельная теорема
22.5. Математическое ожидание. Дисперсия. Среднее квадратическое отклонение
Пусть непрерывная случайная величина задана дифференциальной функцией распределения f(х) и все ее значения принадлежат отрезку [a, b]. Чтобы определить математическое ожидание, разобьем [a, b] на n отрезков длинною х1, х2, ..., хn. Выберем на каждом отрезке произвольную точку хi.
Составим сумму произведений возможных значений хi на вероятность попадания в хi (вероятность попадания в интервал х приближенно равен
f(х)
х.).
![]()
Переходим к пределу
при стремлении наибольшего из отрезков
хi
к нулю получим определенный интеграл
![]()
Определение.
Математическим
ожиданием непрерывной случайной величины
Х,
возможные значения которой принадлежат
отрезку [a,
b],
называют определенный интеграл М
(Х)=![]() Если возможные значения принадлежат
всей оси, то М
(Х)=
Если возможные значения принадлежат
всей оси, то М
(Х)=![]() Математическое ожидание называют
центром распределения вероятностей
случайной величины.
Математическое ожидание называют
центром распределения вероятностей
случайной величины.
Определение. Дисперсией непрерывной случайной величины Х называют математическое ожидание квадрата ее отклонения:
Д (Х)=![]() ,
если возможные значения принадлежат
[a,
b]
и
,
если возможные значения принадлежат
[a,
b]
и
Д (Х)=![]() ,
если возможные значения принадлежат
всей оси.
,
если возможные значения принадлежат
всей оси.
Определение.
Среднее
квадратическое отклонение (стандарт)
непрерывной случайной величины
определяется равенством
(х)=![]()
Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных случайных величин сохраняется и для непрерывных.
Замечание 2. Можно получить для вычисления дисперсии более удобные формулы
Д (Х)=![]() Д (Х)=
Д (Х)=![]()
22.6. Начальные и центральные моменты
Начальные и центральные моменты для непрерывных случайных величин определяются также, как и для дискретных
к=М
(Хк)=![]() (22.2.)
(22.2.)
к=М
[X–M
(X)]к=![]() (22.3.)
(22.3.)
Как говорилось выше, 1=М (Х) характеризует среднее по вероятности значение непрерывной случайной величины Х или центр рассеяния.
1=0, 2= Д(Х) и характеризует меру рассеяния значений случайной величины относительно среднего значения или центра рассеяния.
22.7. Коэффициент асимметрии
3 - третий центральный может служить для характеристики асимметрии (или «скошенности») распределения.
Дело в том, что нечетные моменты для распределения, симметричного относительно математического ожидания, равны 0, как интегралы (см. (7.3.)) от нечетной функции в симметричных пределах.
Если же распределение не симметрично относительно математического ожидания, то подынтегральная функция в интеграле (7.3.) не является симметричной относительно математического ожидания и интеграл (7.3.) 0, если к - нечетное.
Естественно поэтому в качестве характеристики асимметрии рассмотреть какой-либо из нечетных центральных моментов.
1=0
для любых распределений. 3
- наиболее
простой из нечетных центральных моментов.
Он имеет размерность куба случайной
величины. Чтобы получить безразмерную
характеристику асимметрии, 3
делят на
3
и берут в качестве «коэффициента
асимметрии»
или просто «асимметрии»
величину: Аs=![]()
Как связаны между собой тип кривой распределения и коэффициент асимметрии поясняют рисунки 1–3.
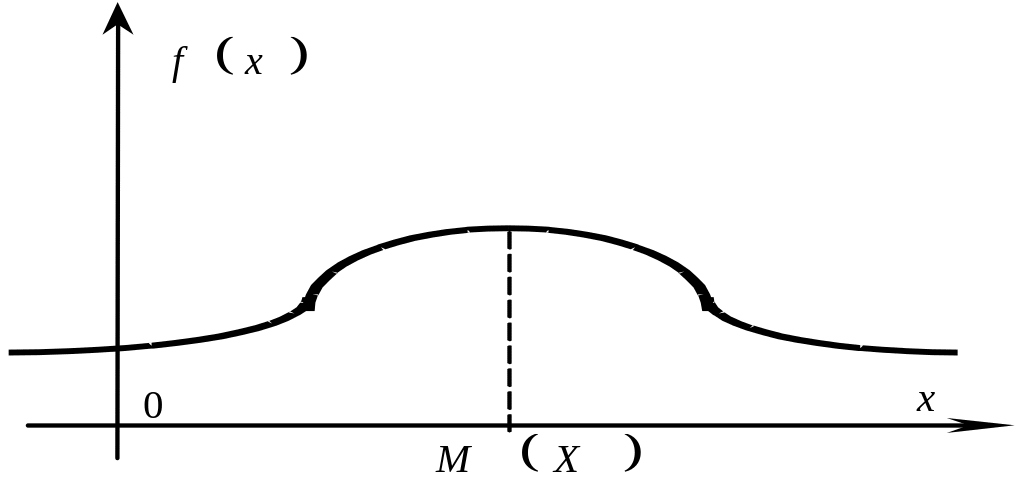
Рис. 1. Симметричное распределение (Аs=0)
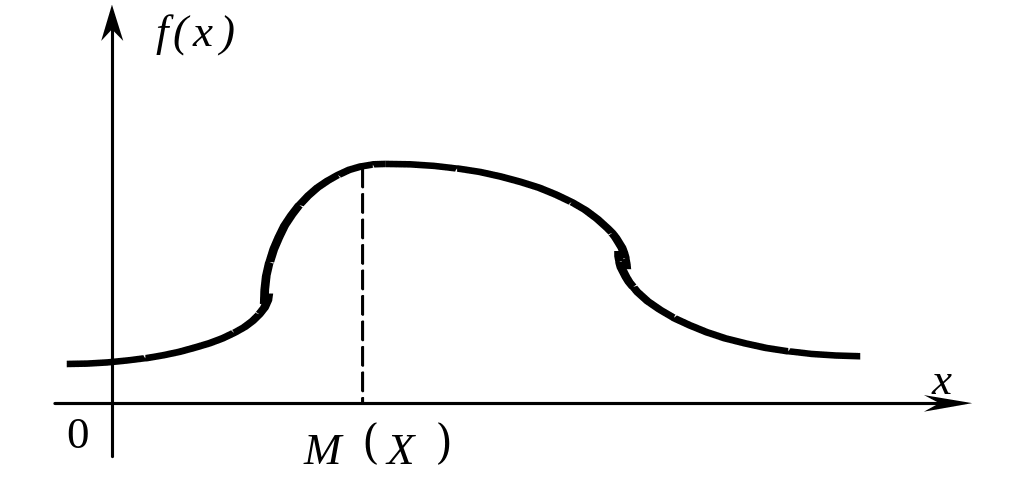
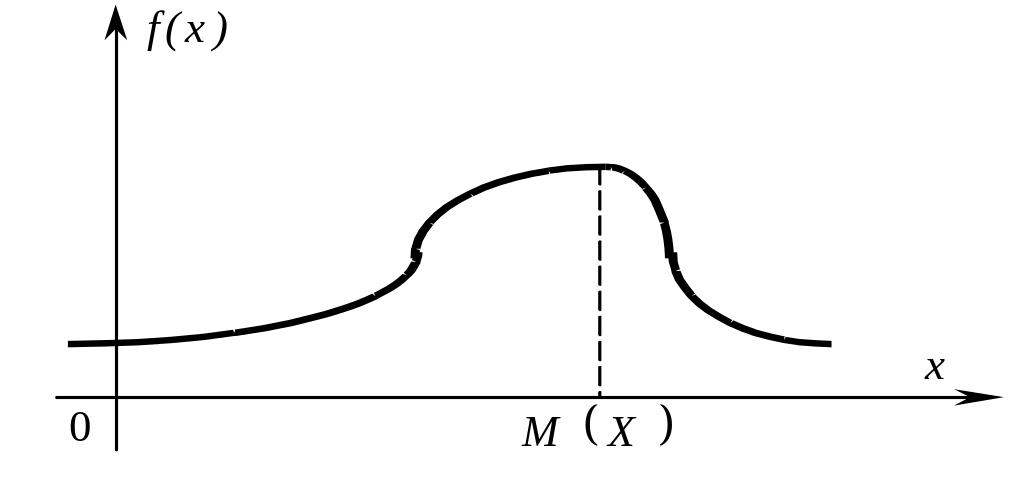
Рис.2. Более «длинная» ветвь Рис 3. Более «длинная» ветвь
кривой справа (Аs>0) кривой слева (Аs<0)
