23.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на интервал [
Определим Р (<X<), если Х - имеет нормальное распределение
Р (<X<)=F ()–F()
Найдем F(х).
(23.5)
(23.6)
Интеграл (23.6.) не
выражается через элементарные функции,
но его можно выразить через специальную
функцию, выражающую определенный
интеграл от
или
,
так называемый интеграл
вероятностей или функцию Лапласа,
для которой составлены таблицы.
Иногда требуется вычислить вероятность попадания случайной величины в интервал, симметричный относительно М (Х)=а.
Пусть его длина 2 l, т.е.
Р (a–l<X<a+l)=
Итак,
Р
(a–l<X<a+l)=Р(|х
-а|<
l)=2Ф*
(23.7.)
Пример. Систематическая ошибка удерживания высоты самолетом +20 м, случайная ошибка имеет среднее квадратическое отклонение 75 м. Для полета самолета отведен коридор высотой 100 м. Какова вероятность того, что самолет будет лететь внутри коридора, если ему задана высота, соответствующая середине коридора.
Решение. а=20 м, =75 м.
Случайные ошибки подчиняются, как правило, нормальному закону.
- Высота коридора.
=-50, =50
Р (-50<X<50)=Ф*
=
=
23.4. Правило трех сигм
Возьмем в формуле (23.7) l=3, тогда
Р (|Х-
а|)<3)=2Ф*
=2Ф*(3)=2
0,49865=0,99730
- очень
большая вероятность.
И, следовательно, вероятность получить значение случайной величины, отличается более чем на 3 от а, очень мала и равна 0,0027, т.е. это событие практически невозможно. В этом и состоит сущность правила трех сигм:
если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. |Х–а|<3 .
Лекция 24. Система случайных величин
24.1. Понятие о системе случайных величин
В практических применениях теории вероятностей часто приходится сталкиваться с задачами, в которых результат опыта описывается не одной, а двумя и более случайными величинами, образующими систему. Например, точка попадания снаряда характеризуется двумя случайными величинами - абсциссой и ординатой. Точка разрыва дистанционного снаряда характеризуется тремя координатами, каждая из которых - случайная величина.
При стрельбе группой из n выстрелов совокупность точек попадания на плоскости может рассматриваться как система 2n случайный величин (n - абсцисс и n - ординат). Условимся систему нескольких случайных величин X, Y, ..., W обозначать (X, Y, ..., W). Свойства системы не исчерпываются свойствами отдельных случайных величин, входящих в систему. Они определяются также взаимными связями (зависимостями) случайных величин. Удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин (Х, Y) можно изображать случайной точкой на плоскости или случайным радиус-вектором.
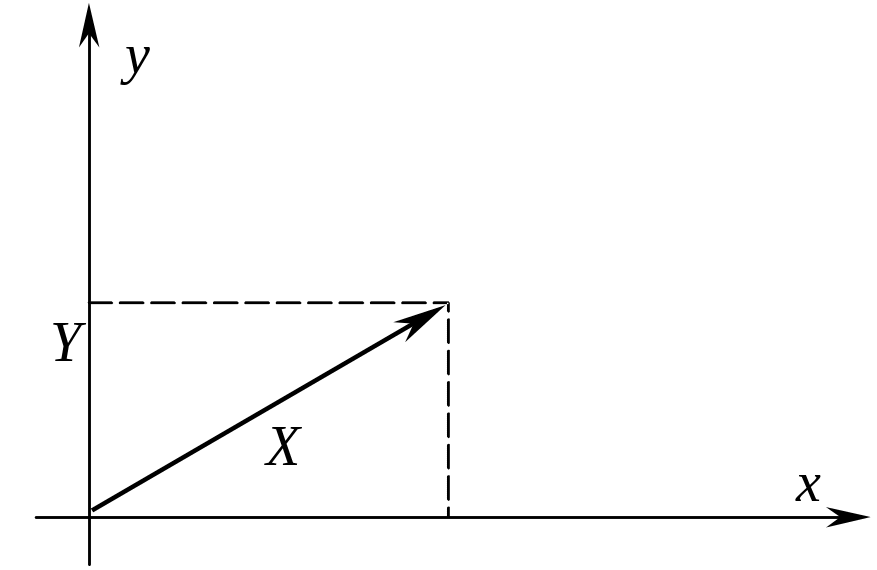
Соответственно, систему 3-х случайных величин (X, Y, Z) или n случайных величин (X, Y, ..., W) можно изображать случайной точкой или случайным вектором в 3-х мерном или n - мерном пространстве.
Нужно различать системы дискретных и непрерывных случайных величин.
Часто системы (Х, Y) и (X, Y, ..., W) называют соответственно двумерной и многомерной случайной величиной.