
- •1. Понятие функции. Ограниченные функции
- •2. Функции нечетные, четные, монотонные
- •3. Числовые последовательности. Определение и примеры
- •5) Словесным описанием.
- •6) Табличным способом.
- •4. Предел числовой последовательности
- •5. Теоремы о пределах числовой последовательности
- •Расходящиеся последовательности:
- •6. Раскрытие неопределенностей 0/0, ∞-∞
- •7.( В конспекте)
- •8. Понятие предела функции
- •9. Вычисление пределов
- •10. Первый замечательный предел и связанные с ним пределы
- •11. Второй замечательный предел и связанные с ним пределы
- •12. Бесконечно большие и бесконечно малые функции
- •13. Бесконечно малые функции одного порядка, эквивалентные бесконечно малые
- •14. Односторонние пределы
- •15. Непрерывность функции в точке и на множестве
- •16. Классификация точек разрыва
- •17. Свойства непрерывных функций
- •18. // В конспекте
- •19. Производная функции в точке
- •20. Правила дифференцирования
- •25. Производная сложной функции
- •26. Производная обратной функции
- •28. Производная функции, заданной неявно и параметрически
- •29. Дифференциал функции, инвариантность формы 1-го дифференциала
- •30. Производные высших порядков. Ф-ла Лейбница
- •31. Дифференциалы высших порядков
- •32. Геометрический смысл производной. Уравнение касательной и нормали
- •33. Теорема Ролля
- •34. Теорема Лагранжа
- •36. Экстремум функции одной переменной. Необходимое условие экстремума
- •37. Достаточные условия экстремума
- •38. Выпуклость, вогнутость графика функции, точки перегиба
- •39. Достаточные условия перегиба
- •40. Асимптоты графика функции
- •41. Правило Лопиталя
- •42. Формула Тейлора для функции
- •43. Комплексные числа. Алгебраическая форма записи комплексного числа
- •44. Действия над комплексными числами в алгебраической форме
- •45. Векторы, линейные операции над векторами
- •46. Координаты вектора
- •47. Определители 2-го, 3-го порядков и их вычисление
- •48. Свойства определителя
- •49. Теорема о разложении определителя
- •50. Линейная зависимость векторов
- •51. Скалярное произведение векторов и его свойства
- •52. Векторное произведение векторов и его свойства
- •53. Смешанное произведение векторов и его свойства
- •54. Уравнение плоскости в пространстве
- •55. Уравнение прямой на плоскости
- •56. Уравнение прямой в пространстве
- •56. Уравнение прямой и плоскости в пространстве
- •58. Кривые второго порядка: эллипс, парабола, гипербола
- •59. Поверхности второго порядка
- •60. Матрицы и действия над ними
- •61. Системы линейных уравнений. Правило Крамера
- •62. Обратная матрица. Условие существования обратной матрицы
- •63. Вычисление обратной матрицы
- •64. Ранг матрицы. Вычисление ранга матрицы
- •65. Теорема Кронекера
37. Достаточные условия экстремума
Для того, чтобы определить точки экстремума используют достаточные условия (признаки экстремума).
Теорема 3 (первый признак экстремума функции).
Пусть – критическая точка непрерывной функции .
Если в некоторой окрестности точки выполняется условие
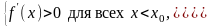
то – точка локального максимума;
если выполняется условие

то – точка локального минимума.
Если производная
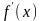 имеет один и тот же знак в левой и правой
полуокрестности точки
,
то
не является точкой экстремума.
имеет один и тот же знак в левой и правой
полуокрестности точки
,
то
не является точкой экстремума.
Теорема 4 (второй признак экстремума функции).
Пусть
– критическая точка функции
,
дважды дифференцируемой в окрестности
точки
.
Тогда
является точкой локального минимума
функции
,
если
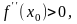 и точкой локального максимума, если
и точкой локального максимума, если
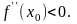
Теорема 5 (третий признак экстремума функции).
Пусть
– n
раз непрерывно дифференцируемая в
критической точке
функция и
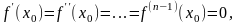
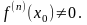 Тогда:
Тогда:
1) если n
– четное и
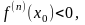 то
– точка локального максимума;
то
– точка локального максимума;
2) если n
– четное и
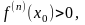 то
– точка локального минимума;
то
– точка локального минимума;
3) если n – не четное, то не является точкой локального экстремума.
38. Выпуклость, вогнутость графика функции, точки перегиба
Определение 8. Множество точек на плоскости называется выпуклым, если отрезок, соединяющий любые две точки этого множества, целиком содержится в этом множестве.
Примерами выпуклых множеств являются : треугольник, отрезок, полуплоскость, вся плоскость.
Определение 9. Функция y = f(x) называется выпуклой вниз (вверх) на множестве X, если для всех x1,x2 X выполняется неравенство
f(1 x1+2x2)1f(x1)+ 2f(x2) (f(1 x1+2x2)1f(x1)+ 2f(x2)),
где 1 0,2 0, 1+2 = 1.
Графики функций, выпуклых вниз и вверх, изображены на рис. 25.
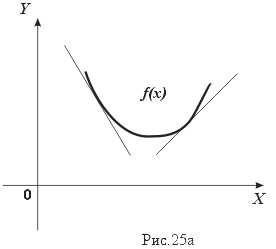
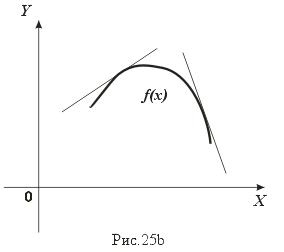
Справедлива
Теорема 9. Функция выпукла вниз (вверх) на множестве X тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает (убывает).
Геометрический смысл теоремы состоит в том, что если f'(x) возрастает (убывает) на множестве X, то возрастает (убывает) угол наклона касательных к графику (рис.26). Это и означает выпуклость функции вниз (вверх).
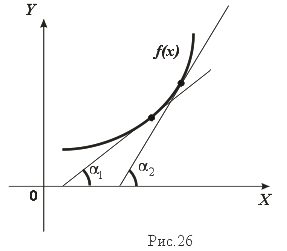 Приведем
достаточное условие выпуклости функции
вниз (вверх).
Приведем
достаточное условие выпуклости функции
вниз (вверх).
Теорема 10 (достаточное условие выпуклости). Если вторая производная дважды дифференцируемой функции положительна (отрицательна) на множестве X, то функция выпукла вниз (вверх) на этом множестве.
Доказательство. Если f''(x)>0, x X, то f'(x) возрастает на множестве X и по предыдущей теореме функция выпукла вниз на множестве X. Аналогично рассматривается случай, когда f''(x)<0.
Необходимое условие выпуклости слабее: если функция выпукла вниз (вверх) на множестве X, то f''(x) 0, x X (или f''(x) 0 ) x X. Например, функция y = x4 выпукла вниз на всей числовой прямой, но y'' = 12x2 обращается в ноль при x = 0.
Определение 10 (точка перегиба). Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция имеет разные направления выпуклости.
Нетрудно заметить, что точки перегиба - это точки экстремума первой производной. Отсюда следуют утверждения.
Теорема 11 (необходимое условие перегиба). Вторая производная f''(x) дважды непрерывно дифференцируемой функции в точке перегиба x0 равна нулю, т.е. f''(x0) = 0.
//--------------------
График функции
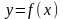 называется вогнутым
(выпуклым вниз) на
называется вогнутым
(выпуклым вниз) на
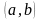 ,
если дуга кривой
на этом интервале расположена выше
любой касательной проведенной к графику
этой функции (рис. 1).
,
если дуга кривой
на этом интервале расположена выше
любой касательной проведенной к графику
этой функции (рис. 1).

Рис. 1.
График функции называется выпуклым (выпуклым вверх) на , если дуга кривой на этом интервале расположена ниже любой касательной проведенной к графику этой функции (рис. 2).

Рис. 2.
Теорема 6.
Если функция
дважды дифференцируема на
и

 всюду на этом интервале, то график
функции вогнут (выпуклый) на
.
всюду на этом интервале, то график
функции вогнут (выпуклый) на
.
Точка
така, что график функции
меняет выпуклость на вогнутость или
наоборот, проходя через
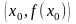 ,
называется точкой
перегиба
(рис. 3)
,
называется точкой
перегиба
(рис. 3)
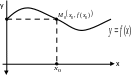
Рис. 3.
Для нахождения
точек перегиба вначале находят критические
точки 2-го рода
– те значения x,
для которых
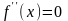 или
или
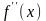 не существует. Далее используют
достаточные условия перегиба.
не существует. Далее используют
достаточные условия перегиба.
Теорема 7 (достаточные условия перегиба).
Если для функции вторая производная в некоторой точке обращается в нуль или не существует и при переходе через нее меняет свой знак, то – точка перегиба.
