5. Теоремы о пределах числовой последовательности

Согласно определению предела последовательности можно лишь доказать, что определенное число (которое уже найдено) является пределом последовательности.

Для нахождения этого предела используют свойства сходящихся последовательностей и следующую теорему, которая показывает, как находить предел от арифметических операций над последовательностями.

Теорема. Пусть последовательности и имеют пределы, тогда

1. 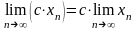, где 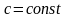– постоянная выносится за знак предела.

2. 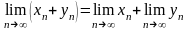– предел суммы равен сумме пределов.

3. – предел произведения равен произведению пределов.

4. 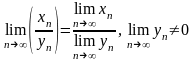– предел частного равен частному пределов.

Заметим, что формулы 2 и 3 обобщаются на произвольное конечное число слагаемых или множителей. Если таких слагаемых или множителей бесконечно много, то переход от предела суммы (произведения) к сумм6е (произведению) пределов может привести к ошибке.

При вычислении пределов сначала пробуют непосредственно выяснить, к чему стремиться величина, стоящая под знаком предела, при условии . Для этого используют также указанную теорему.

Если же в результате таких рассуждений приходят к выражениям типа

,

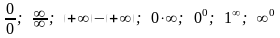то предел считается не найденным. Говорят, что получена неопределенность одного из этих типов.

Для того, чтобы устранить неопределенность и вычислить предел, необходимо выражение, стоящее под знаком предела преобразовать тождественно, чтобы неопределенность исчезла.

По определению предел является числом. Однако неограниченна последовательность не может стремиться к конечному числу. При возрастании 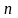ее значения бесконечно возрастают по модулю и стремятся к или к 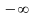. В таком случае считаю, что последовательность не имеет предела.

Однако это записывают с помощью символа :

, .

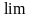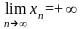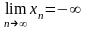Такие последовательности называют бесконечно большими.

В отношении предела последовательности возможен еще один случай: вообще невозможно определить, к чему стремиться последовательность. Например последовательность .

Таким образом все последовательности делятся следующим образом:

1. Сходящиеся последовательности – имеют предел, равный конечному числу.

2. Расходящиеся последовательности:

1. Бесконечно большие последовательности.

2. Последовательности, для которых предел не определен.

//---------------------

Теорема 1. Если последовательность { a _n } имеет предел, то этот предел единственный.

Теорема 2. Для того чтобы последовательность сходилась к числу , a необходимо и достаточно, чтобы выполнялось равенство a_n=a+α_n, где lim α_n=0.

Теорема 3. Предел алгебраической суммы двух сходящихся последовательностей равен алгебраической сумме пределов этих последовательностей, т.е.

6. Раскрытие неопределенностей 0/0, ∞-∞

Для раскрытия неопределённостей типа 0/0 существует следующий алгоритм:

• Разложение на множители числителя и знаменателя;

• Сокращение дроби.

Неопределенность ∞-∞ сводится к ∞/∞

7.( В конспекте)

8. Понятие предела функции

Рассмотрим функцию , определённую в некоторой окрестности точки (в самой точке 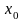данная функция может быть не определена).

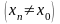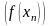Число А называется пределом функции в точке ,если для любой последовательности , сходящейся к , последовательность соответствующих значений функции сходится к А.

Обозначается:

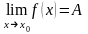
или

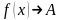при

Если функция в точке имеет предел, то он единственный.

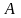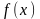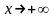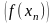Кроме предела функции в точке рассматривают предел функции на бесконечности: число называется пределом функции при (или ), если для всякой последовательности , (или ) при последовательность соответствующих значений функции сходится к числу .

Обозначают:

.
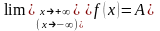