14. Односторонние пределы

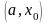
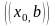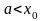
Левой (правой) полуокрестностью точки называется произвольный интервал , где 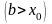слева (справа).

Число А называется пределом функции в точке слева (справа), если функция определена в некоторой левой (правой) полуокрестности точки и если для любого 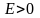существует 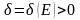такое, что для всех 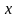, удовлетворяющих условию 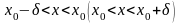, выполняется неравенство

.

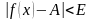В этом случае пишут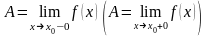

Пределы слева и справа называются односторонними пределами. Если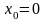 , то односторонние пределы обозначают , .

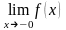Функция имеет предел в точке тогда и только тогда, когда в этой точке существуют оба односторонние предела, равные между собой.

В этом случае их общее значение и является пределом функции в точке

.

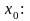
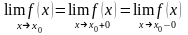15. Непрерывность функции в точке и на множестве

Функция называется непрерывной в точке , если она определена в этой точке в некоторой ее окрестности и

(27)

Если функция непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.

Существуют и другие определения непрерывности функции в точке. Функция называется непрерывной в точке , если она определена в этой точке и в некоторой ее окрестности и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке:

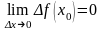(28)

Непрерывность функции в точке определяется также на основе односторонних предметов.

Функция называется непрерывной в точке , если она определена в этой точке и некоторой ее окрестности и существует односторонние пределы (конечные) такие, что

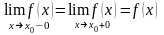(29)

16. Классификация точек разрыва

Классификацию точек разрыва дают в зависимости от того, какое условие последнего определения непрерывности (в том числе равенства (29)) нарушено.

Точки разрыва I рода

1. Если существуют односторонние пределы в точке (конечные) и

,

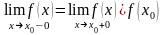то называется точкой устранимого разрыва.

2. Если существует односторонние пределы в точке (конечные) и

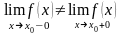, (44)

то - точка разрыва, который называется скачок.

В случае устранимого разрыва функцию можно доопределить в точке значением и она станет непрерывной.

В случае скачка сделать это невозможно.

Точки разрыва II рода

1. Ес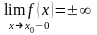ли

или

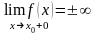
то – точка разрыва, который называется бесконечный скачок. В этом случае прямая является вертикальной асимптотой.

2. Если односторонние пределы в точке не существуют (не определены), то - точка неопределенности.

17. Свойства непрерывных функций

Свойства непрерывных функций

1. Если функции и непрерывны в точке , то их сумма 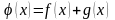также есть непрерывная функция в точке . Это свойство справедливо для любого конечного числа слагаемых.

2. Произведение двух непрерывных функций есть функция непрерывная.

3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

4. Если функция непрерывна в точке и 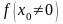, то значения функции в некоторой окрестности точки имеют тот же знак, что и .

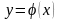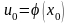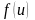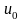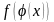5. Если функция непрерывна в точке и принимает в этой точке значение , а функция непрерывна в точке , то сложная функция непрерывна в точке .

6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

7. Если непрерывная на некотором обрезке функция принимает на его концах значение разных знаков, то на этом отрезке найдется хотя бы одна точка, в которой .

8. Если функция непрерывна в точке , то операция вычисления предела в этой точке и функции 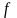переставимы, т.е.

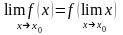(30)

На свойстве 8 (равенства (30)) и было основано непосредственное вычисление предела функции в случае отсутствия неопределенности (см.параграфы 16.1 – 16.4).

Если нарушается хотя бы одно условие, указанное в определении непрерывности, то называется такой разрыв функции.