
- •1. Понятие функции. Ограниченные функции
- •2. Функции нечетные, четные, монотонные
- •3. Числовые последовательности. Определение и примеры
- •5) Словесным описанием.
- •6) Табличным способом.
- •4. Предел числовой последовательности
- •5. Теоремы о пределах числовой последовательности
- •Расходящиеся последовательности:
- •6. Раскрытие неопределенностей 0/0, ∞-∞
- •7.( В конспекте)
- •8. Понятие предела функции
- •9. Вычисление пределов
- •10. Первый замечательный предел и связанные с ним пределы
- •11. Второй замечательный предел и связанные с ним пределы
- •12. Бесконечно большие и бесконечно малые функции
- •13. Бесконечно малые функции одного порядка, эквивалентные бесконечно малые
- •14. Односторонние пределы
- •15. Непрерывность функции в точке и на множестве
- •16. Классификация точек разрыва
- •17. Свойства непрерывных функций
- •18. // В конспекте
- •19. Производная функции в точке
- •20. Правила дифференцирования
- •25. Производная сложной функции
- •26. Производная обратной функции
- •28. Производная функции, заданной неявно и параметрически
- •29. Дифференциал функции, инвариантность формы 1-го дифференциала
- •30. Производные высших порядков. Ф-ла Лейбница
- •31. Дифференциалы высших порядков
- •32. Геометрический смысл производной. Уравнение касательной и нормали
- •33. Теорема Ролля
- •34. Теорема Лагранжа
- •36. Экстремум функции одной переменной. Необходимое условие экстремума
- •37. Достаточные условия экстремума
- •38. Выпуклость, вогнутость графика функции, точки перегиба
- •39. Достаточные условия перегиба
- •40. Асимптоты графика функции
- •41. Правило Лопиталя
- •42. Формула Тейлора для функции
- •43. Комплексные числа. Алгебраическая форма записи комплексного числа
- •44. Действия над комплексными числами в алгебраической форме
- •45. Векторы, линейные операции над векторами
- •46. Координаты вектора
- •47. Определители 2-го, 3-го порядков и их вычисление
- •48. Свойства определителя
- •49. Теорема о разложении определителя
- •50. Линейная зависимость векторов
- •51. Скалярное произведение векторов и его свойства
- •52. Векторное произведение векторов и его свойства
- •53. Смешанное произведение векторов и его свойства
- •54. Уравнение плоскости в пространстве
- •55. Уравнение прямой на плоскости
- •56. Уравнение прямой в пространстве
- •56. Уравнение прямой и плоскости в пространстве
- •58. Кривые второго порядка: эллипс, парабола, гипербола
- •59. Поверхности второго порядка
- •60. Матрицы и действия над ними
- •61. Системы линейных уравнений. Правило Крамера
- •62. Обратная матрица. Условие существования обратной матрицы
- •63. Вычисление обратной матрицы
- •64. Ранг матрицы. Вычисление ранга матрицы
- •65. Теорема Кронекера
51. Скалярное произведение векторов и его свойства
Кроме линейных операций, для векторов определено также скалярное произведение.
Скалярным
произведением
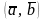 двух ненулевых векторов
и
называется число
двух ненулевых векторов
и
называется число
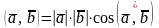 .
.
Скалярное
произведение обозначается также
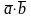 .
.
Если хотя бы один
из векторов
или
нулевой, то
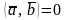 .
.
Скалярным квадратом вектора называется величина
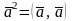 .
.
Физический
смысл скалярного произведения двух
векторов
состоит в том, что оно численно равно
работе, осуществляемой силой
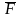 по
перемещению материальной точки на
вектор
по
перемещению материальной точки на
вектор
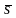 ,
то есть
,
то есть
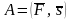 .
.
Для вычисления угла между векторами и можно воспользоваться формулой
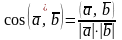 .
.
Свойства скалярного произведения:
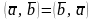 –
коммутативность;
–
коммутативность;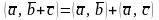 –дистрибутивность;
–дистрибутивность;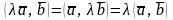 ;
;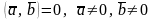 тогда и только
тогда, когда
тогда и только
тогда, когда
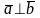 ;
;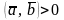 тогда и только
тогда, когда
тогда и только
тогда, когда
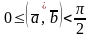 ,
,
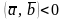 тогда и только
тогда, когда
тогда и только
тогда, когда
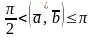
6)
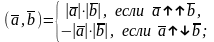
7)
 .
.
52. Векторное произведение векторов и его свойства
Векторным
произведением
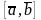 двух векторов
и
называется вектор, удовлетворяющий
следующим условиям:
двух векторов
и
называется вектор, удовлетворяющий
следующим условиям:
1)
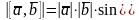 ;
;
2)
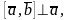
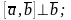
3) тройка векторов
 – правая.
– правая.
Векторное
произведение обозначают также
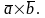
Если хотя бы один
из векторов
или
нулевой, то
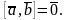
Геометрический смысл векторного произведения состоит в том, что длина этого вектора численно равна площади параллелограмма, построенного на векторах и :
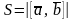 .
.
Физический
смысл
векторного произведения состоит в том,
что момент
 силы
силы
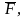 приложенной к точке A,
относительно точки O
есть векторное произведение векторов
приложенной к точке A,
относительно точки O
есть векторное произведение векторов
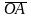 и
т. е.
и
т. е.
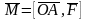 .
.
Свойства векторного произведения:
1)
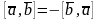 ;
;
2)
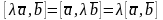 ;
;
3)
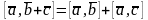 ;
;
4)
 при
при
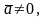
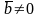 тогда и только тогда, когда векторы
и
коллинеарны.
тогда и только тогда, когда векторы
и
коллинеарны.
Если
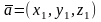 и
и
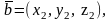 то
то
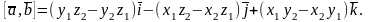
Последнюю формулу удобно записать в виде формального определения третьего порядка:
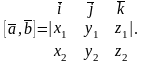
53. Смешанное произведение векторов и его свойства
Смешанным
произведением
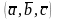 трех векторов
трех векторов
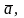 и
называется число, определяемое
соотношением
и
называется число, определяемое
соотношением
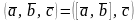 .
.
Если хотя бы один
из векторов
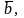 – нулевой, то их смешанное произведение
равно нулю.
– нулевой, то их смешанное произведение
равно нулю.
Геометрический смысл смешанного произведения векторов состоит в том, что его абсолютное значение равно объему V параллелепипеда, построенного на векторах приведенных к общему началу:
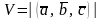 .
.
Свойства смешанного произведения
1)
 ;
;
2)
 ;
;
;
3)
 ,
где
,
где
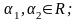
4)
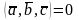 при
при
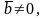
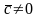 тогда и только тогда, когда
– компланарные векторы;
тогда и только тогда, когда
– компланарные векторы;
5) векторы
образуют базис в трехмерном пространстве
при условии
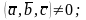
6) если
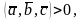 то векторы
образуют правую тройку; если
то векторы
образуют правую тройку; если
 – левую.
– левую.
В случае, когда
векторы
заданы в ортонормированном базисе
координатами
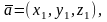
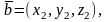
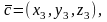 их смешанное произведение может быть
найдено по формуле
их смешанное произведение может быть
найдено по формуле
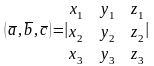 .
(10)
.
(10)
54. Уравнение плоскости в пространстве
Пусть P
– плоскость,
уравнение которой надо записать,
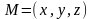 –
произвольная точка плоскости.
–
произвольная точка плоскости.
1. Если задана точка
 плоскости Р
и два некомпланарных вектора
плоскости Р
и два некомпланарных вектора
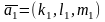 и
и
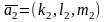 ,
параллельных данной плоскости, то
справедливы следующие уравнения
плоскости Р
,
параллельных данной плоскости, то
справедливы следующие уравнения
плоскости Р
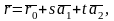 (1)
(1)
где
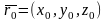 – радиус-вектор точки
– радиус-вектор точки
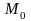 ,
,
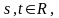 называется векторно-параметрическим
уравнением
плоскости
P.
Запись уравнения (1) в координатной форме
называется векторно-параметрическим
уравнением
плоскости
P.
Запись уравнения (1) в координатной форме
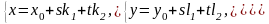 (2)
(2)
называется параметрическими уравнениями плоскости.
Плоскость можно задать уравнением
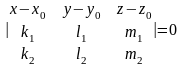 .
(3)
.
(3)
2. Если известны
три точки плоскости P,
не лежащие на одной прямой:
,
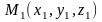 ,
,
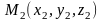 ,
то имеем уравнение
плоскости, проходящей через
три заданные
точки :
,
то имеем уравнение
плоскости, проходящей через
три заданные
точки :
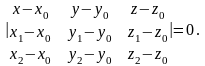 (4)
(4)
3. Если известны точки пересечения плоскости P с координатными осями, т. е. M0(a, 0, 0), M1(0, b, 0), M2(0, 0, c), то справедливо уравнение плоскости «в отрезках»:
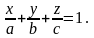 (5)
(5)
4.
Если задан нормальный
вектор
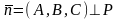 и точка
и точка
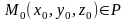 ,
то справедливо уравнение
,
то справедливо уравнение
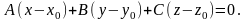 (6)
(6)
После преобразования последнего уравнения приходим к общему уравнению плоскости P:
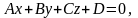
где
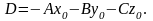
5. Если в качестве
нормального вектора плоскости P
взять единичный вектор
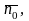 направленный из начала координат в
сторону плоскости, то
направленный из начала координат в
сторону плоскости, то
 где
где
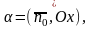
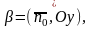
 Тогда справедливо нормальное
уравнение
плоскости
Тогда справедливо нормальное
уравнение
плоскости
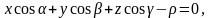 (7)
(7)
где
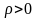 – расстояние от начала координат до
плоскости.
– расстояние от начала координат до
плоскости.
Величина
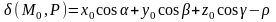 ,
(8)
,
(8)
где
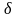 называется отклонением
точки
называется отклонением
точки
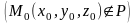 от
плоскости
от
плоскости
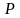 .
При этом:
.
При этом:
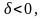 если
и O(0,
0, 0) лежат по одну сторону от плоскости;
если
и O(0,
0, 0) лежат по одну сторону от плоскости;
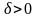 – если лежат по разные стороны;
– если лежат по разные стороны;
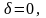 если
если
 Расстояние
Расстояние
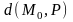 от точки
до плоскости
равно абсолютному значению ее отклонения,
т. е.
от точки
до плоскости
равно абсолютному значению ее отклонения,
т. е.
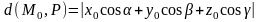 .
.
От общего уравнения плоскости к нормальному можно перейти с помощью умножения на нормирующий множитель
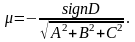 (9)
(9)
Расстояние
от точки
до плоскости
 заданной общим уравнением
может быть найдено по формуле
заданной общим уравнением
может быть найдено по формуле
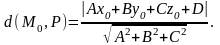 (10)
(10)
Угол
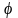 между плоскостями в пространстве
определяется по косинусу угла между
нормальными векторами
между плоскостями в пространстве
определяется по косинусу угла между
нормальными векторами
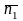 и
и
 этих плоскостей:
этих плоскостей:
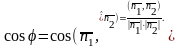 (11)
(11)
