61. Системы линейных уравнений. Правило Крамера

Система линейных алгебраических уравнений (или линейная система) имеет вид:

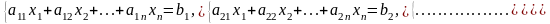(1)

где a_ij и b_j –заданные числа.

Эту систему можно записать в матричной форме

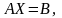(2)

где – матрица системы состоящая из коэффициентов a_ij,

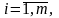
B – матрица-столбец свободных элементов b_j,

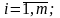
X – матрица-столбец неизвестных, т. е. такая, которая обращает матричное уравнение (2) в равенство (является решением этого уравнения).

Система (1) называется совместной, если у нее существует хотя бы одно решение, в противном случае она называется несовместной. Две системы называются эквивалентными (равносильными), если множества их решений совпадают.

Ответ на вопрос о совместимости системы дает теорема Кронера-Копелли: для того чтобы система (1) была совместной, необходимо и достаточно, чтобы

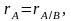
где 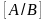– расширенная матрица системы (1), т.е. матрица свободных членов.

Рассмотрим систему 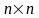, имеющую вид:

(3)

или в матричном виде

где

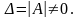
Методы решения

Метод обратной матрицы состоит в решении матричного уравнения

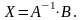
Метод Крамера: для нахождения неизвестных необходимо использовать формулы

(4)

где

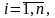
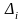– определитель, получаемый из определителя 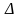системы (3) заменой i-го столбца столбцом свободных членов.

Формулы (4) называются формулами Крамера.

Решение произвольной линейной системы (1) из m уравнений и n неизвестных начинается с нахождения ранга. Пусть 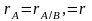и система (1) сведена к эквивалентной системе

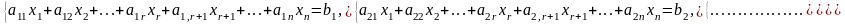(5)

Если 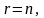то система (5) имеет единственное решение, которое можно получить указанными выше методами, если 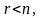то существует бесконечное множество решений. Для его получения неизвестные x₁, x₂, …, x_r называют базисными, x_r+1, x_r+2, …, x_n – свободными, система (5) записывается в виде:

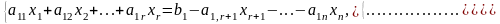
Последняя система решается, например, методом Крамера.

Метод Гаусса

Для решения произвольных систем используют метод Гаусса. С помощью элементарных преобразований над строками расширенную матрицу системы (1) приводят к виду:

Соответствующая ей система, равносильная (1), примет вид:

(6)

Если хотя бы одно из чисел b_{r + 1}, … b_m отлично от нуля, то система (6), а значит, и исходная система (1) несовместны.

Если b_{r + 1} = … = b_m = 0, то система (6) позволяет получить явное выражение для базисных неизвестных x₁, …, x_r через свободные неизвестные x_{r + 1}, …, x_n.

Если r = n, то свободные неизвестные отсутствуют, а значит, системы (6) и (1) имеют единственное решение.

На практике обычно обходятся приведением матрицы системы (1) к треугольной или трапециевидной форме, после чего значения базисных переменных ищутся в обратном порядке.

62. Обратная матрица. Условие существования обратной матрицы

Квадратная матрица B, удовлетворяющая совместно с заданной матрицей A того же порядка равенствам 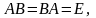называется обратной к A и обозначается A^–1. Обратная матрица A^–1 существует при условии, что A – невырожденная матрица, т. е.