2 1. Метрические пространства. Полные метрич. Пр-тва

О1. Мн-во М наз-ся метрическим пространством если каждой паре его элементов х и у поставлено в соответствие неотр. число (х,у), удов-щее след. условиям (аксиомам):

1. (x,y)=0x=y–акс. тождест-сти;

2. (акс. симметрии):  (х,у) =  (у,х),

3. (акс. треугольника):

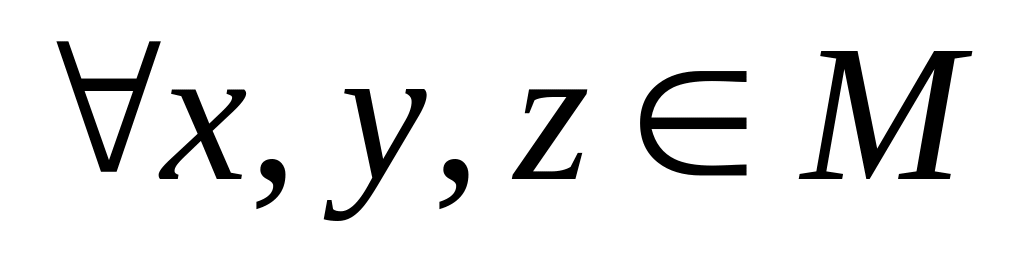
(х,у)≤(x,z)+ (z,y) .

Это акс. метрики. Число (х,у) наз-ся расстоянием.

Пр1: мн-во действ. чисел R образует метр. прост-во с (х,у)=|x-y|, (х,у)≥0.

1. (х,у)=|x-y|=0  x-y=0  x=y

2. (х,у)=|x-y|=|y-x|=(у,x)

3. (х,у)=|x-y|=|(x-z)+(z-y)|≤ |=|x-z|+|z-y|=|= (x,z)+  (z,y)

Пр2: Мн-во непрерыв. ф-ций опред-х на отрезке [a;b] образует метр. пр-во С_[a;b] с расстоянием (х,у)=

Акс. 1 и 2 – очевидны. Акс. 3:

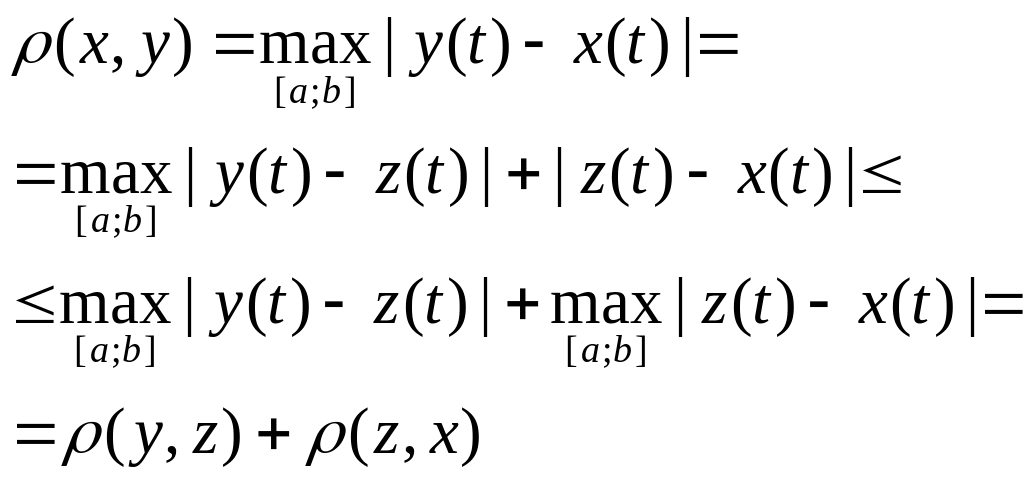О2. Послед-сть {х_п} точек метр.пр-ва Х наз-ся фундаментальной, если она удовл-яет критерию Коши, т.е. для любого >0 сущ-ет N=N( ) такое, что при всех п>N и m>N вып-ся нер-во  (х_п,х_m)< .

Всякая сходящаяся { }-сть яв-ся фунд-ной. Обратное имеет место не всегда.

О3. Если метр-е пр-тво Х таково, что в нем всякая { }-cть сх-ся, то это прост-во наз-ся полным.

Пр3: X=R – есть полное метр. пр-во, т.к. для любого мн-ва действ. чисел справедлив критерий Коши, согласно к-му -ая фунд-ная { }-сть R-чисел яв-ся сходящейся.

Пр4: С_[a;b] - яв-ся полным метр. пр-вом.

2 2. Пр-цип сжимающих отобр-ний

О1. Говорят, что отображение А:М→М имеет неподвижную точку х₀, если Ах₀= х₀.

О2. Отобр-ние f метр-го пр-тва Х в себя наз-ся сжимающим, если 0<α<1 такое, что x, yX вып-ся нерав-во (f(х),f(у))≤ α(х,y) (1).

Всякое сжимающее отобр-ние яв-ся непрерывным. Дейст-но, если х_п→х, т.е. (х_n,n→0,то (1)=>(f(х_n),f(x)))→0=>f(х_n) →f(x)

Т(Банаха)(пр-п сжим. отоб-ний). Всякое сжимающее отобр-ние, опред-ное в полном метр. прост-ве Х имеет 1-у и только 1-у не-подвижную точку (т.е. f(x)=x им. единст. реш-е).

Д. Пусть х₀ Х.. Положим , , …, ,…. Получаем посл-ть точек метр. прост-ва Х. Покажем, что { }-сть яв-ся фундаментальной. Пусть m≥n

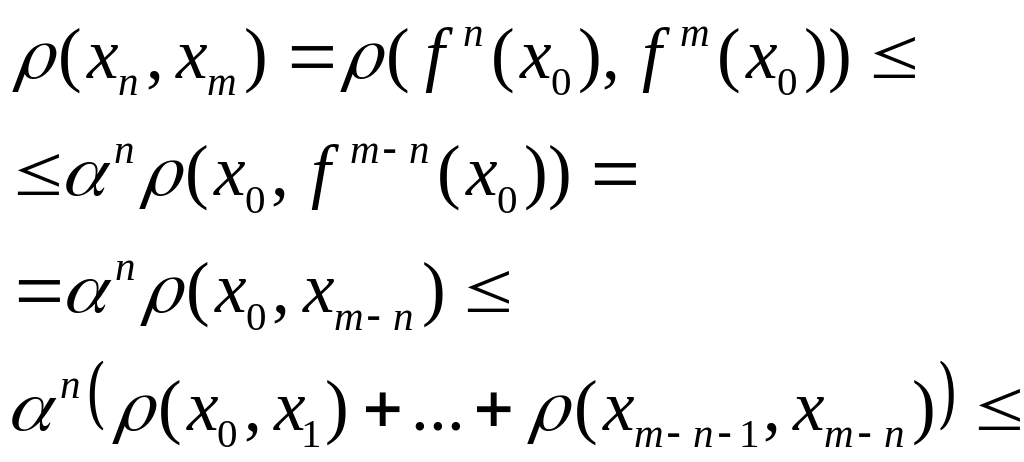
(2).

Т.к. α : 0<α<1=>полученное выраж-е при достаточно большом n будет →0 =>(х_n, х_m)→0 и { }-cть фундаментальна. По условию, Х- полно => {x_n} – сх-ся. x_n→х, n→∞ . Т.к. f-непрерывно, то 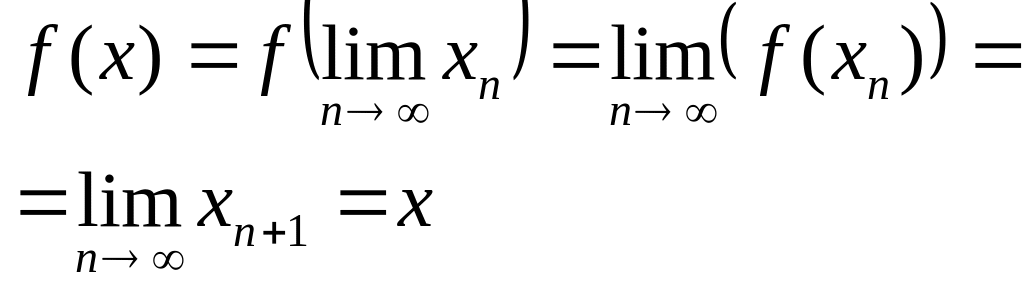=> . Т.о. док-но неподвижность точки. Осталось док-ть ее ед-ть. Пусть и . Т.к. отображениесжимащее=> => => (т.к. ) .

Пр-п сжим-х отбр-ий широко исп-ся при док-ве теорем сущ-ния и единст-сти, решений различных ур-ний.

Продемонстрируем применение при док-ве след.теоремы: Если в диф.у-нии. (3) ф-ция f(x,y) удовл-ет условиям: 1) f(x,y) непрерывна в некот. прямоуг-ке Р:

х₀-а≤х≤ х₀+а; у₀-b≤y≤ у₀+b,

2) f(x,y) удовл-ет усл-ию Липшица по у,

то единст. решение диф. ур. (3) с нач-ми усл-ми , опред-ное и непрерывное на некот. сегменте

[х₀-h; х₀+h].

Д-во: Считая у ф-цией от х, проинтегр-ем обе части (3) от х₀ до х. Т.к. , то 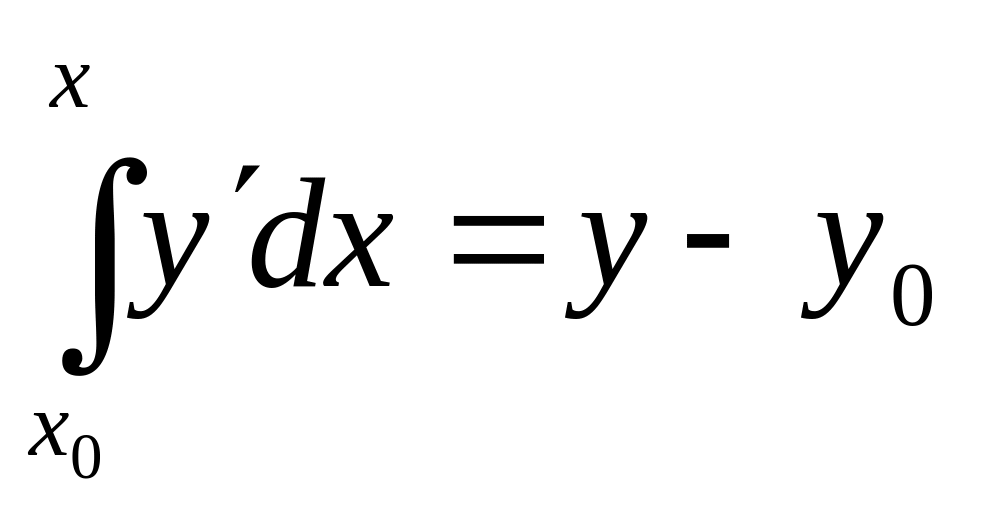и получаем 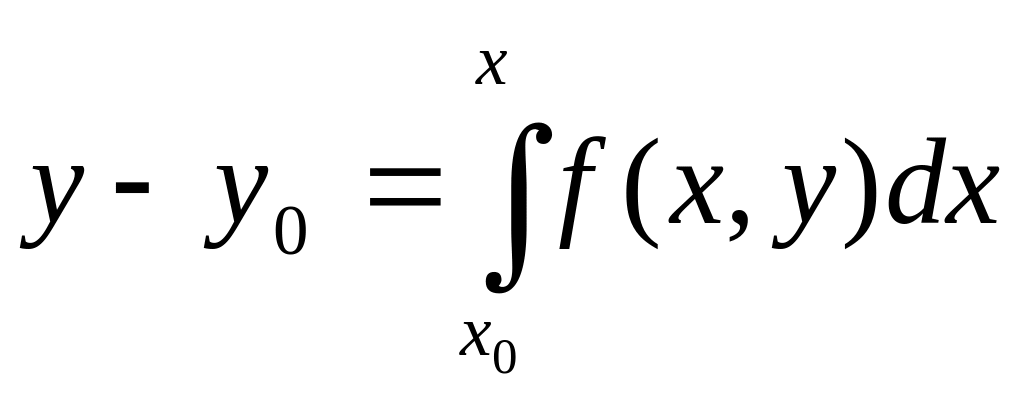(4). Если (4) продиф-ть по х, то получим (3), при этом из (4) при х=х₀ получаем у=у₀.Т.ч.(3) с нач. условиями и (4)-равносильны.

Т.к. f(x,y) непрерывна в замкн. области Р, то постоянная М>0 такая, что |f(x,y)|<M. Кроме того , . Пусть h – любая «+»-ная const, т.ч.

Рассм-м метр. пр-во С непрерыв. ф-ций, заданных на [х₀-h; х₀+h]. Пусть -подмн-во прост-ва С, состоящее из всех ф-ций y=y(x), для к-ых у₀-b≤y≤ у₀+b, при всех х [х₀-h; х₀+h]. В С мн-во замкнуто. Но -полное метр. пр-во, как замкнутое подпр-во полного метр. пр-ва С.

Рассм-м отображение 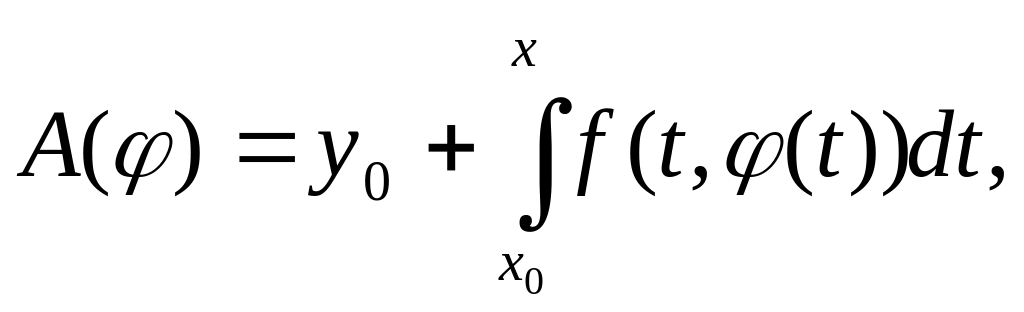х [х₀-h; х₀+h]. Оно переводит в себя. Действ-во, пусть . 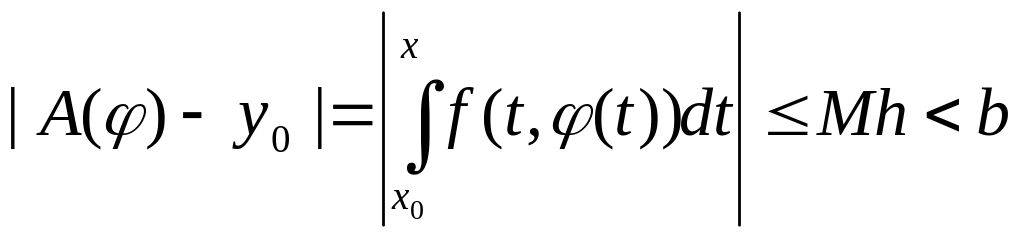, т.е. . Отоб-ние А яв-ся сжимающим в . Имеем

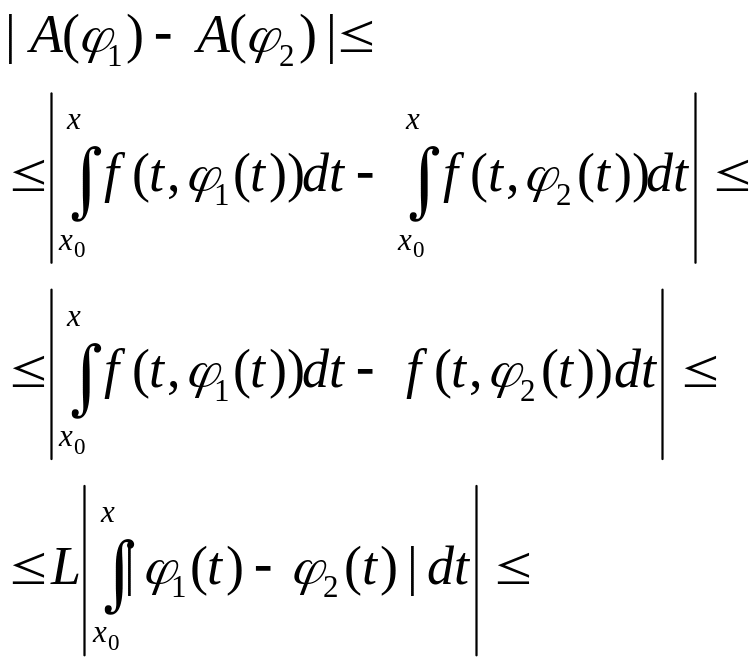
где α=Lh<1. Итак,

По принципу сжим. отоб-ний ур-ние у=А(у), т.е. (4) имеет 1 и только 1 решение в пр-ве . ЧТД.