7. Разложение функций sin X и cos X в степенной ряд. Синус и косинус в комплексной области

Запишем ряд Маклорена для ф-ции f(x) = sin x. Отсюда получ-ся, что f(0) = 0; f’(0) = 1; f’’(0) = 0; f’’’(0) = -1,… .Имеем ряд .

По признаку Даламбера ряд сх-ся при всех х  (-, +). Исследуем остаточный член в форме Лагранжа:

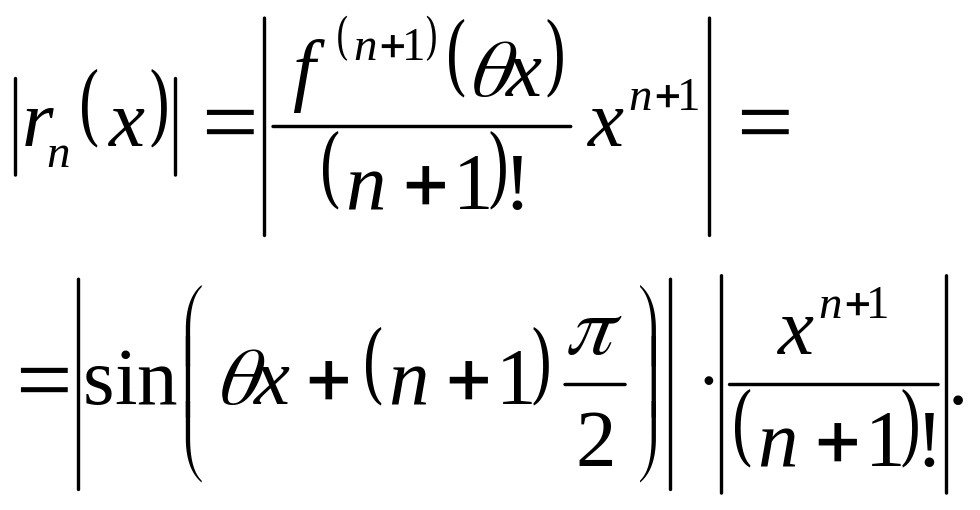
Здесь первый множитель ограничен, а второй  0 при n  , т. к. яв-ся абс-ой величиной (n + 1)-го члена разложениям е^х. Значит, при всех х и ряд сх-ся к sin x при всех х  (-, +). (1)

Диф-руя (1) почленно, получаем (2)

Ф-лы (1), (2) можно использовать для вычисления значений и для всех х  (-, +) с любой точно-стью. При вычислении можно ограни-читься значениями углов |x|<π/4, т. к. значения для других углов наход-ся при помощи формул приведения.

Т. к. ряды (1) и (2) знакочередую-щиеся, то по признаку Лейбница остаток ряда не превышает (n + 1)-го члена, что облегчает оценку погрешности вычислений.

По опред-ию , (3)

О ба ряда сх-ся при всех z. Радиус сх-сти R=∞. Пользуясь фор-ми (3) можно получить все св-ва триг-х ф-ий. То же можно получить с помощью формул Эйлера. В теории рядов для действительных х доказано , => , , x  R.

Для компл-го z по опред-ию полагаем, , , z  C (4)

Формулы (4) наз-ся форм-ми Эйлера. Из (4) => св-ва тригон-х ф-ций:

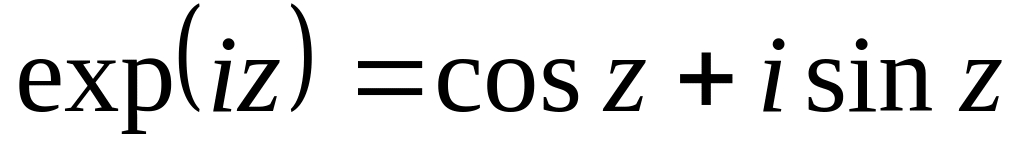1. , z  C

2. ,

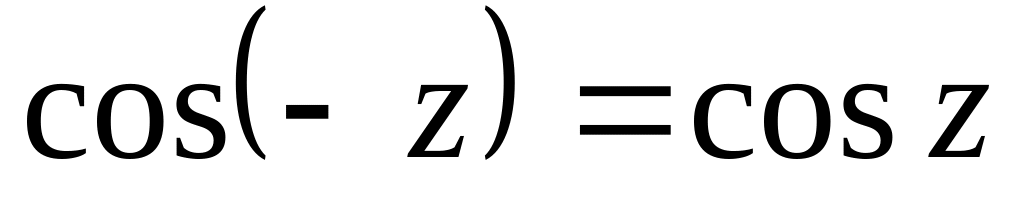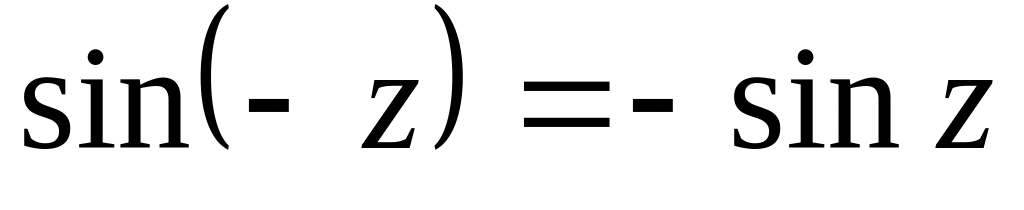
3. Обе функции имеют период 2π,

т. к. имеет период 2π.

4.

(5)

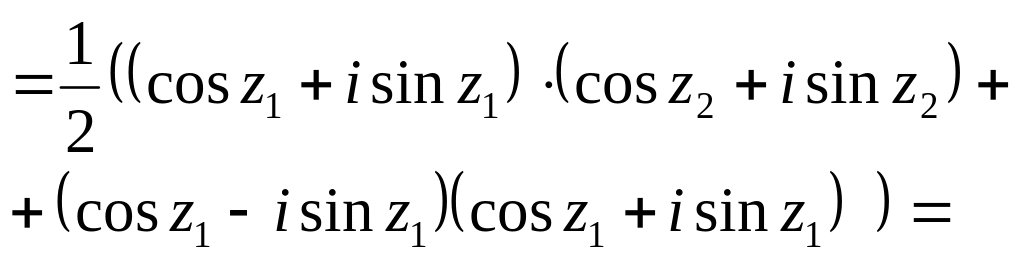
Ан-но для (5)

5. Положив z₁ = z, z₂ = -z из (5) получим . Но из неё не => что , 6.

8. Дифференцируемые функции. Правила дифференцирования

О1. Если отношение имеет предел при х  0, то он наз-ся производной ф-ции f(x) в точке х₀.

Этот предел можно искать  х₀  D_f, если он .  х  D_f будет соот-вать опред-ое значение , то этот предел будет некот-й ф-цией от х. Эта ф-ция наз-ся производной ф-ции f(x). Операция вычисления производ-ной наз-ся операцией дифференци-рования или дифференцированием.

Пусть ф-ция у = f(x) непрерывна в рассм-ой точке x и у = f(х + х) - f(x). Если х0, то у0, т. е. обе эти ве-личины – ∞-но малые при х0. Возьмем в качестве основной б.м. х и выделим для у главную часть у = А(х)^k + ((х)^k) (А ≠ 0, k > 0). Пусть k = 1, т. е. х и у –одного порядка и запишем у = Ах + (х) (1)

О2. Ф-ция f(x) наз-ся дифференц-ой в т. x_, если приращение ф-ции в этой точке у = f(х + х) - f(x) представимо в виде (1), где А – const, не завися-щая от х. Величина Ах наз-ся дифференциалом ф-ции f(x) в т. x. Диффер-циал обозн-ся у=dy+○(х).

Ф-ция f(x) диф-на в точке х  у одного порядка или более высокого порядка, чем х, т.е. ≥1.

Т. 1. Ф-ция у = f(x) диффер-руема в т. хона имеет в этой точке производ-ную, причем

Т. 2. Если ф-ции и имеют производные в т. х₀, то их сумма также имеет производную, причем , т. е. произ-водная суммы = сумме производных.

Т.3. Если и имеют производные в т. х₀, то произведение имеет производную в точке х₀, причем .

Т. 3. Если и имеют произв-ные в т. х₀, причем то частное имеет производную в точке х₀, .

Д. , , .

Отсюда . Ч. т. д.