20. Формула и ряд Тейлора.

] ф-я f(x) в т.х₀ имеет n произ-ых. Выясним, ли мн-н степени не выше n, т.ч. и при этом … (1)

Будем искать этот многочлен в виде (2)

Подставив х=х₀ в (2), находим , т.е. согл.(1).

Продиф-ем (2): (3)

В (3) при х=х₀ , т.е. согласно (1). Диффер-уя еще раз и подставив х=х₀ находим . Диф-уя n-раз, получим . В итоге имеем

Мн-н удов-ет (1) по построению.

Проверим условие . Пусть Из (1)=> По правилу Лопиталя

Значит, . Этим доказана

Т₁: ] ф-ция f(x) определена на (a;b), x₀ (a;b) и f(x) в т. x₀ имеет производные до n-го порядка включ-но=>

(4)

(4)-ф-ла Т-ра ф-ции f(x) в т. x₀ с остаточ. членом в форме Пеано.

P_n(x)-мн-н Т-ра, r_n(x)= f(x)-P_n(x) – остат. член ф-лы Т-ра. Если в (4) x=0, то получим: ф-лу Маклорена:

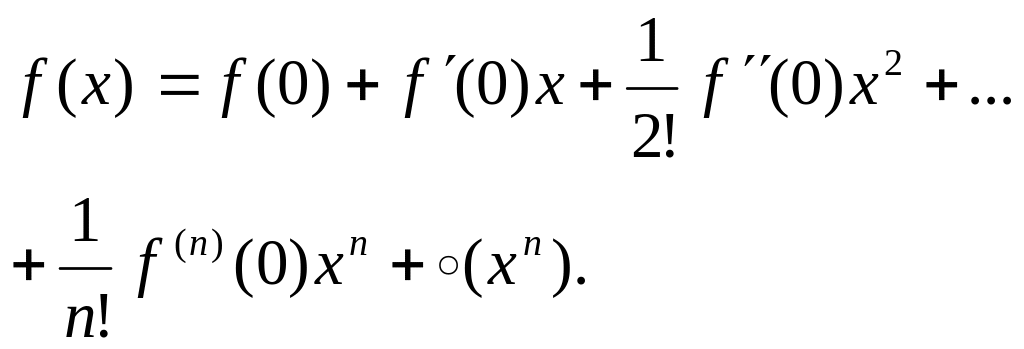
] f(x)- f(x₀)=Δy, x- x₀=Δx=dx. Тогда

Тогда (4) примет вид:

Остат. член ф-лы Т-ра можно записать в различ.форме:

1. 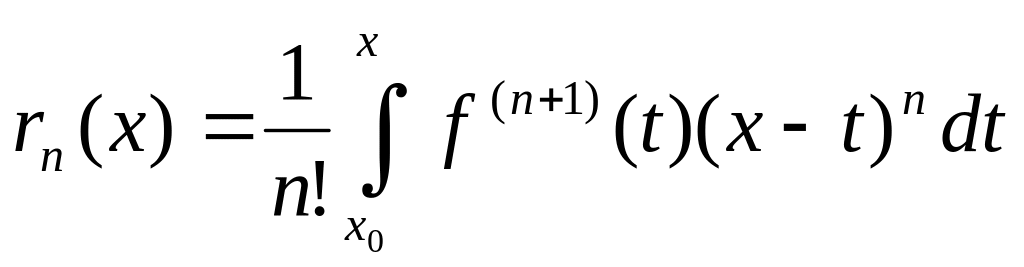- интеграль. форма.

2. 0<θ<1-форма Лагранжа

3. - форма Коши

О₁:] ф-я f(x) определена в некот-й окр-ти т. х₀ и имеет в этой т. произв-ые всех порядков. Тогда (7)-наз-ся рядом Т-ра для ф-ии f(x) в т. х₀. Т. к. сумма степ-го ряда с радиусом сх-сти r>0 внутри интервала сх-сти яв-ся ∞-но диффер-мой ф-цией, то степ-й р. можно разложить только беск-но дифф-ую ф-цию. Однако не всякая ∞-но диф-мая ф-ция разлагается в степ. ряд.

Т₁: Если ф-ция f(x) м/б разложена в степ-й р. в т. х₀, то такое разложение единст-е.

Д-во:] f(x) в т. х₀ разлагается в степ-й р. , r>0. Найдем последовательно и полагаем x=х₀. Получим . Это означает, что искомый ряд есть р.Т-ра ф-ии f(x) в т. х₀ .Коэф-ты ряда опред-ся значениями f(x) и ее производных в т. х₀ однозначно. Значит, разложение в ряд единственно. ■

Т.о. если ф-ция f(x) представима степ. рядом, то этот ряд есть р.Т-ра. Возможны случаи:

1) радиус сх-сти р.Т-ра r>0 и его сумма = f(x), т.е. f(x) разлагается в степ.р.;

2) r>0, но сумма ряда ≠ f(x);

3) r=0. В 2) и 3) f(x) не разлагается в степ.р.

Т₂: Чтобы р.Т-ра ф-ции f(x) сх-ся к f(x) на некот. интервале, необх-мо и дост-но, чтобы остаточный член ф-лы Т-ра для f(x)|→ к 0 при n→∞ при всех x из этого интервала.

Д-во: Запишем ф-лу Т-ра для ф-ции f(x): (8)

Обозначив частич.суммы р.(7) ч/з , ф-лу (8) запишем в виде Видим, что если то т.е. сумма р.(1) = f(x).

Обратно, пусть сумма ряда (7) = f(x). Тогда ЧТД.

Т₂ позволяет решать задачи на разложение ф-ций в р.Тейлора. Это разложение производ-ся примерно по след. плану.

1. найти послед-но производные ф-ции f(x).

2. Вычислить 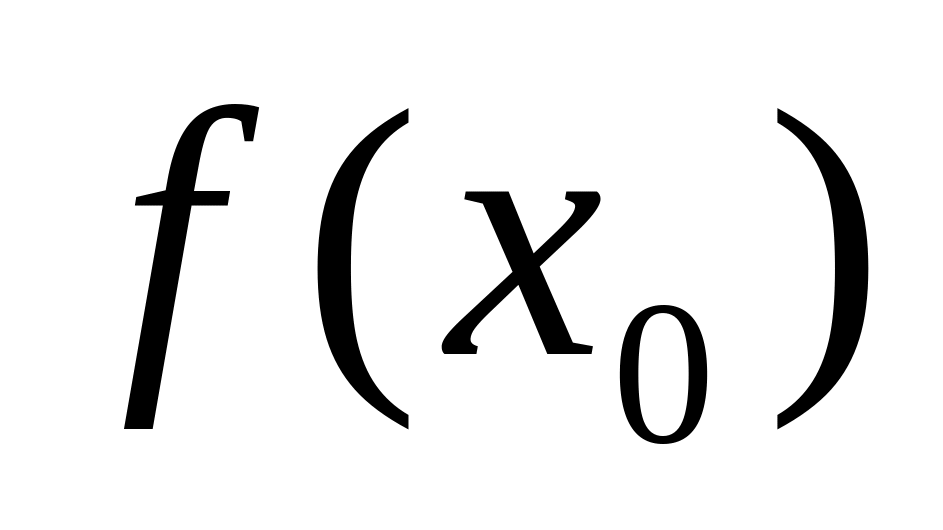и (n=1,2,…)

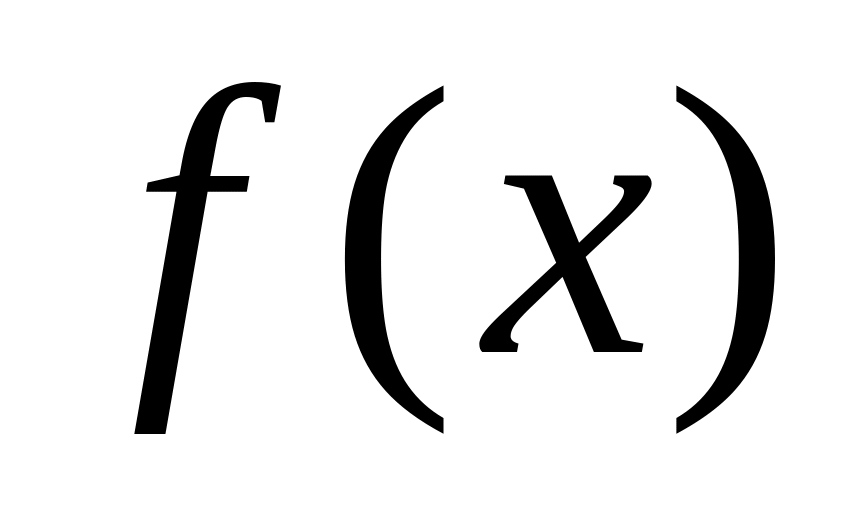
3. Формально записать р.Т-ра: 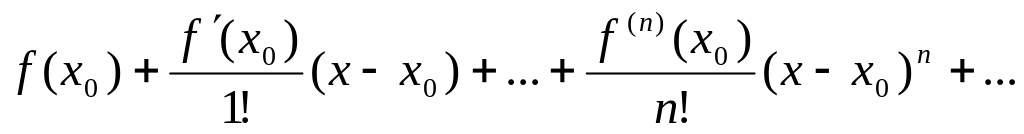.(9)

4. Найти интервал сх-сти этого ряда.

5. Записать остат. член ф-лы Т-ра для f(x).

6. Найти мн-во тех х из интервала сх-сти, для к-рых 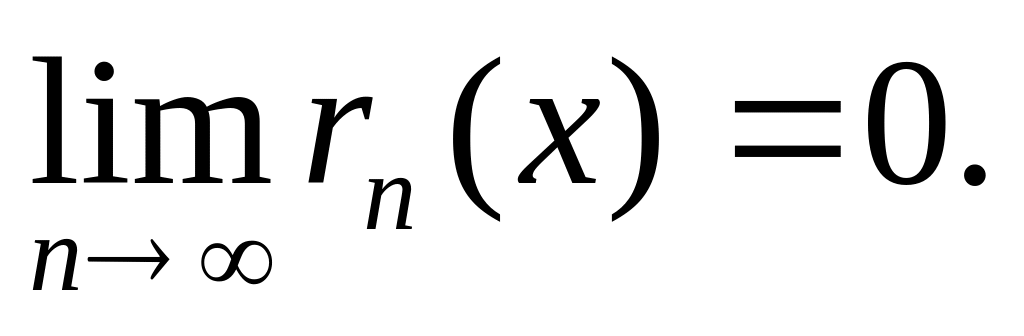Для этих х в разложении (3) мы вправе ~ заменить на =, т.е. записать разложение в р.Т-ра.