
- •1 . Мощность мн-ва. Счётность мн-ва рациональных чисел. Несчётность мн-ва дей-х чисел.
- •2. Предел и непрерывность функций в точке. Св-ва непрерывных функций на отрезке.
- •3 . Предел числовой послед-ности. Теорема Больцано.
- •4. Определение и существование степени с иррациональным показателем.
- •5. Степенная функция с иррациональным показателем. Степень в комплексной области.
- •7. Разложение функций sin X и cos X в степенной ряд. Синус и косинус в комплексной области
- •8. Дифференцируемые функции. Правила дифференцирования
- •9 . Теорема Лагранжа. Условия монотонности и выпуклости функции на промежутке
- •1 0. Экстремумы и точки перегиба
- •12. Опред-ный интеграл. Интегри-руемость непрерывной функции. Формула Ньютона-Лейбниц
- •-Ние первообразной. Формула Ньютона-Лейбница (н.-л.)
- •14. Вычисление s в декартовых и полярных координатах,
- •1 6. Числовые ряды. Признаки сходимости: Даламбера и Коши.
- •17. Абсолютно и условно сх-ся ряды.
- •18.Функциональные послед-ти и ряды.
- •1 9. Степ-ые ряды в компл. Области.
- •20. Формула и ряд Тейлора.
- •2 1. Метрические пространства. Полные метрич. Пр-тва
- •2 3. О.Д.У. Первого порядка. Ур-я с разд-ся пер-ми. Линейные д.У.
- •2 4. Линейные д.У. С пост-ми к-нтами
- •25. Производная ф-ции компл.Пер. Условия диф-ти. Понятие аналитич. Ф-ции
5. Степенная функция с иррациональным показателем. Степень в комплексной области.
Р
ассм-м
степенную ф-цию у
=![]() ,
где
α- иррац-ное число.
,
где
α- иррац-ное число.
Т.к.
допустимы лишь x>0,
то можно записать
![]() .
.
Ф-ция
у
=
яв-ся
сложной, где
![]() .
.
Свойства:
1.
![]()
![]()
![]()
![]()
2. Монотонно возрастает в D(у) при α>0 и убывает при α <0.
Д-во.
Пусть α>0
![]() =>
=>
![]() и
и
![]() .
Т.е.
.
Т.е.
![]() =>
=>![]() =>y1<y2
-
монотонно возрастает. При α<0 аналогично
(монотонно убывает).
=>y1<y2
-
монотонно возрастает. При α<0 аналогично
(монотонно убывает).
3. Непрерывна в D(f) по теореме о непрерывности сложной функции.
4.
![]()
Д-во.
Пусть α>0, тогда при
![]() ,
,
![]() ;
;
![]() .
При α<0
.
При α<0
![]() ;
;![]() .
.
5.
![]()
Д-во.
Пусть α>0
![]() ,
,
![]() ,
,
![]() .
Если α <0
.
Если α <0
![]()
![]() .
.
Степень в комплексной области.
Пусть
а≠0 – любое комп. число. При целом n
![]() ,
,
![]() .
Получаем одно значение степени.
.
Получаем одно значение степени.
Пусть r=p/q – несокр.дробь, т.е. r – рацион. число.
Имеем
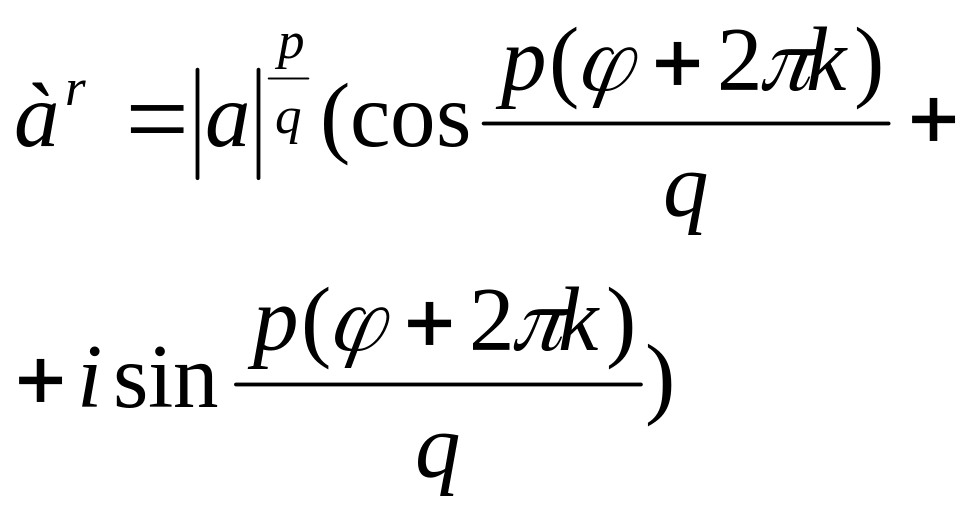 ,
k=0,
1,…,q-1
,
k=0,
1,…,q-1
Имеем
q
значений степени. Запишем
![]() иначе:
иначе:
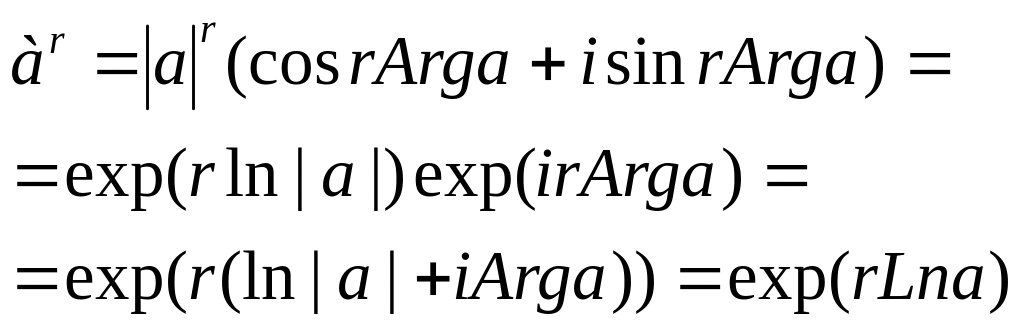
для
примера:
![]()
Для
любых компл-х а и α по опред-ию полагают:
![]() (1) – формула универсальна.
(1) – формула универсальна.
Степень с произв. показателем не подчиняется известным законам умножения и возведения в степень
![]() ,
,
![]()
6. Сущ-е лог-ов. Лог-ая ф-ия. Лог-м в компл-ой области
О1.
Логарифмом числа b
по основанию а
(а
> 0, a
≠ 1) наз-ся показатель степени, в которую
нужно возвести а,
чтобы получить b.
Пишут
![]() .
.
![]() (1)
- основное логар-ое тождество. Возведем
его обе части в степень :
(1)
- основное логар-ое тождество. Возведем
его обе части в степень :
![]() .
Отсюда
.
Отсюда
![]() (2)
(2)
Т1. Для дейст-го числа b>0 логарифм при основании а >0, a≠1.
Д.
Пусть а
> 0, b
> 0. Рассм-м ф-цию y=ax.
Т. к.
![]() ,
,
![]() ,
то, по теореме о промежуточном значении
непрерывной ф-ции, ф-ция у
= ах
принимает
«+»-ное значение. В силу монотонности
ф-ции
значение принимается один раз. След-но,
для любого b
число х, такое что
,
то, по теореме о промежуточном значении
непрерывной ф-ции, ф-ция у
= ах
принимает
«+»-ное значение. В силу монотонности
ф-ции
значение принимается один раз. След-но,
для любого b
число х, такое что
![]() ,
где x=logab.
,
где x=logab.
Случай 0 < a < 1 аналогичен. .
Пусть
теперь с
> 0, с
≠ 1.
![]() согласно (1). Прологарифмируем по
основанию а.
согласно (1). Прологарифмируем по
основанию а.
![]() согласно (2). Отсюда
согласно (2). Отсюда
![]() (3).
Положив в (3) х=а,
находим
(3).
Положив в (3) х=а,
находим
![]() .
.
Рассм-м y = f(x) = logax ( a > 0, a 1). Она обратна по отношению к функции у = ах.
D(y) = (0, +).
loga1 = 0, logaa = 1
Если а>1, то
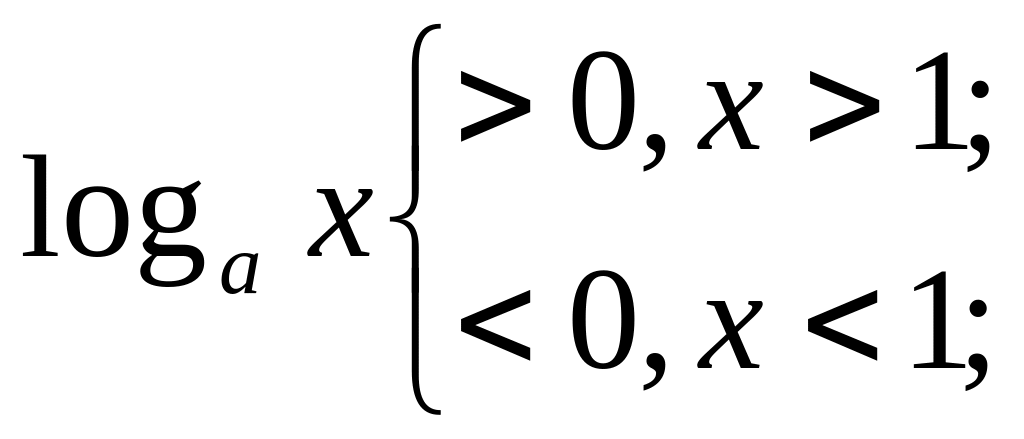 если 0 <a
<1,
то
если 0 <a
<1,
то
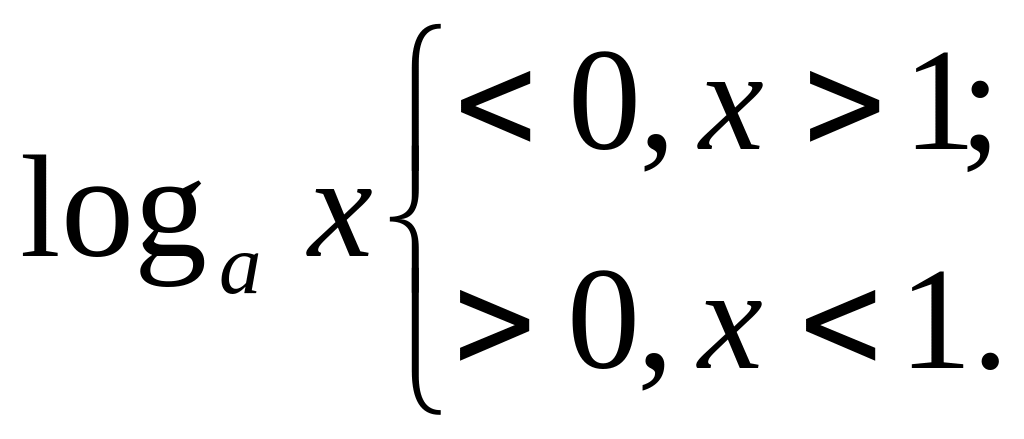
Д.
Пусть а
> 1. Тогда
![]() .
Получили доказуемое в обратном порядке.
Случай 0<a<1
аналогичен.
.
Получили доказуемое в обратном порядке.
Случай 0<a<1
аналогичен.
y = logax непрерывна в D(y) как обратная к непрерывной и монотонной функции y = аx.
При а > 1 монотонно возрастает на (0, +); при 0<a<1 монотонно убывает как обратная ф-ция к y = аx.

Д.
Пусть а>1.
В
![]() при х+
будет logax+
согласно св-ву ф-ции y
= аx.
При 0<a<1=>
logax-
.
при х+
будет logax+
согласно св-ву ф-ции y
= аx.
При 0<a<1=>
logax-
.
Д. Пусть а > 1. В при х+0 будет logax-. При 0 < a < 1 отсюда же logax+ .
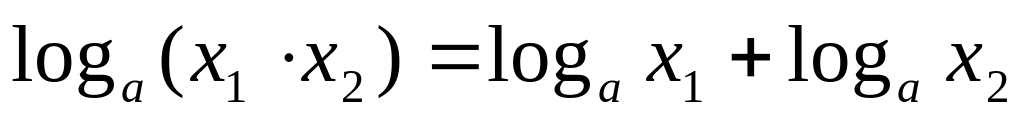 ,
(х1
>
0, x2
> 0).
,
(х1
>
0, x2
> 0).
Д.
![]() ,
,
![]() .
.
![]() и далее по определению логарифма.
и далее по определению логарифма.
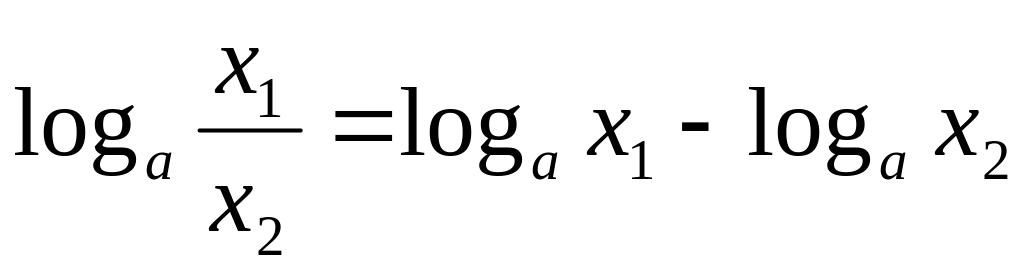 ,
,
(х1 > 0, x2 > 0).
 ,
(х>0,
R).
,
(х>0,
R).
Число w наз-ся логарифмом числа z, если expw = z. Пишут w = Lnz.
Св-ва логарифмов:
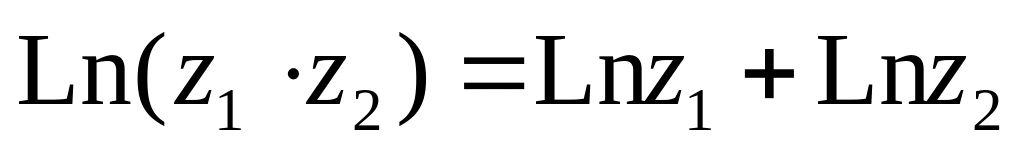 ,(z1≠0,z2≠0)
,(z1≠0,z2≠0)
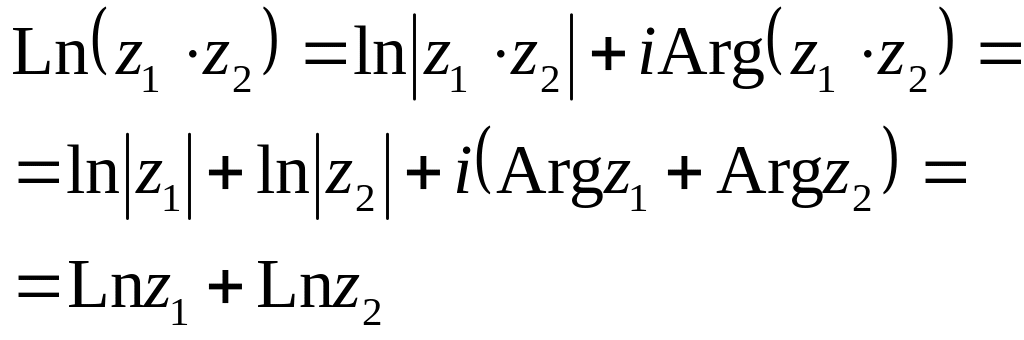
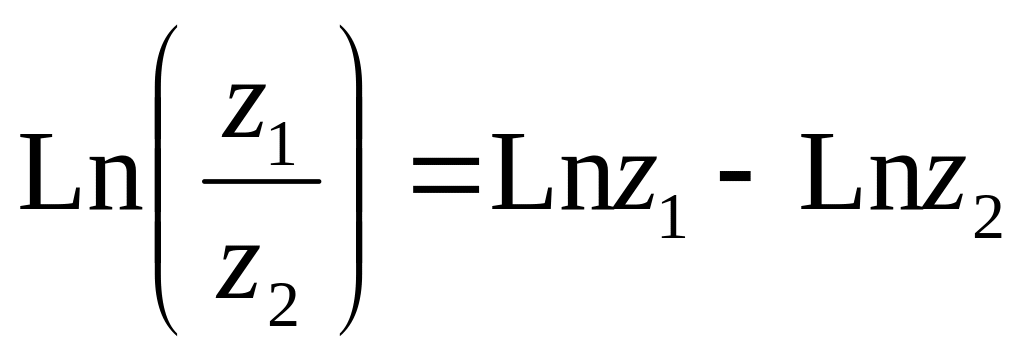 ,
(z1≠0,
z2
≠ 0)
,
(z1≠0,
z2
≠ 0)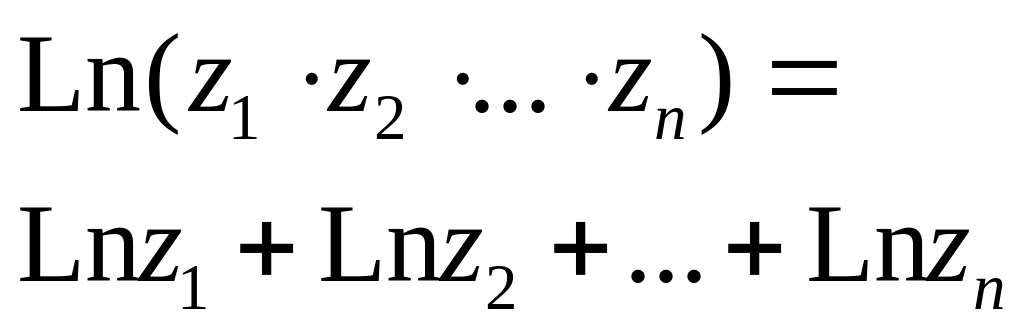 ,(zk≠0,k)
,(zk≠0,k)
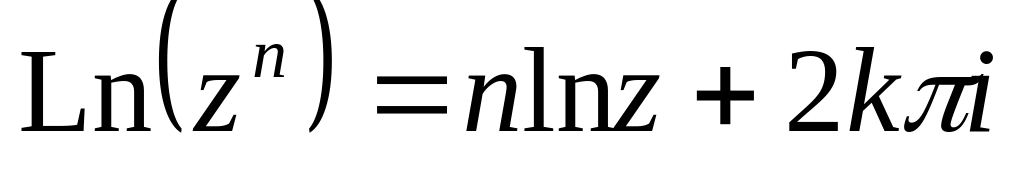
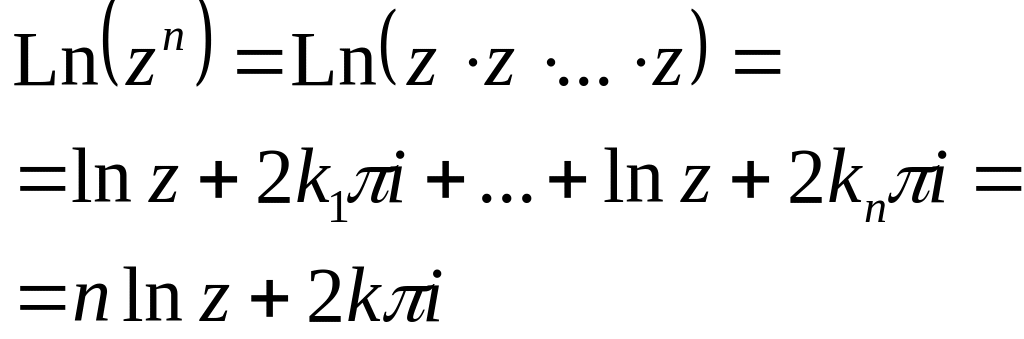 Для
главных значений логарифмов (ln)
не вып-ся даже св-ва 1 и 2, т. к. мнимая
часть левой и правой частей должна
лежать в (-π, π].
Для
главных значений логарифмов (ln)
не вып-ся даже св-ва 1 и 2, т. к. мнимая
часть левой и правой частей должна
лежать в (-π, π].
