18.Функциональные послед-ти и ряды.

] дана ∞-ная посл-ть ф-ций f₁(x),f₂(x),…,f_n(x),…(1) на нек-м мн-ве М.

О₁: Если для конкретного x₀ M получим сх-ся числ-ю { }-сть (f_n(x₀)), то говорят, что функ-ая { }-сть (1) сх-ся в т. x₀ или что x₀ – точка сх-сти { }-сти (1). Если получаем рассх-ся числ-ю { }-сть (f_n(x₀)), то x₀ – точка рассх-сти

О₂: Если конеч-й предел то этот предел яв-ся некот. ф-цией от х, к-рый обозначим ч/з f(x) и назовем предель-ной ф-цией, т.е. .

Предельная ф-ция f(x) опред-на на мн-ве Р. Ан-но рассм-ся ряды, члены к-го некот. ф-ции опред. на мн-ве М.

Ряд вида (2)- наз-ся функц-м.

О₃:Если р. (2) сх-ся при x=x₀ M, то т. x₀ наз-ся т-й сх-ти р.(2). А мн-во всех т-к сх-ти р.(2) наз-ся обл-ю сх-ти функ-го р.(2) Если же р. (2) рассх-ся при x=x₀ M, то т. x₀ наз-ся т-й рассх-ти р.(2).

О₄:Если {s_n(x)} – послед-сть частич. сумм р.(2), тогда - пред-я ф-я для {s_n(x)} и в тоже время S(x) - яв-ся суммой р.(2).

Пусть на М заданы f(x) и g(x).

О₅: наз-ся расстоя-нием по Чебышеву м/у ф-циями f(x) и g(x) на М и обозначается , т.е. =

Пусть на М задана {f_n(x)}, сходящаяся при пред. ф-ции f(x), т.е. .

Возьмем некот. x₀ Р, тогда .

По опред. предела числ. { }-сти имеем , , т.ч. вып-ся нер-во

Если взять другое значение , то при том же ε номер N будет уже другим, т.е.N зависит не только от ε, но и от х.

О₆: Функ-я посл-ть (f_n(x)) н-ся равномерно сх-ся к f (x) на мн-ве Р, если , , т.ч. вып-ся сразу .

Учитывая О_6, м. записать эквив. опред.

О_6.1: Функ-я посл-ть (f_n(x)) н-ся равномерно сх-ся к f (x) на мн-ве Р, если

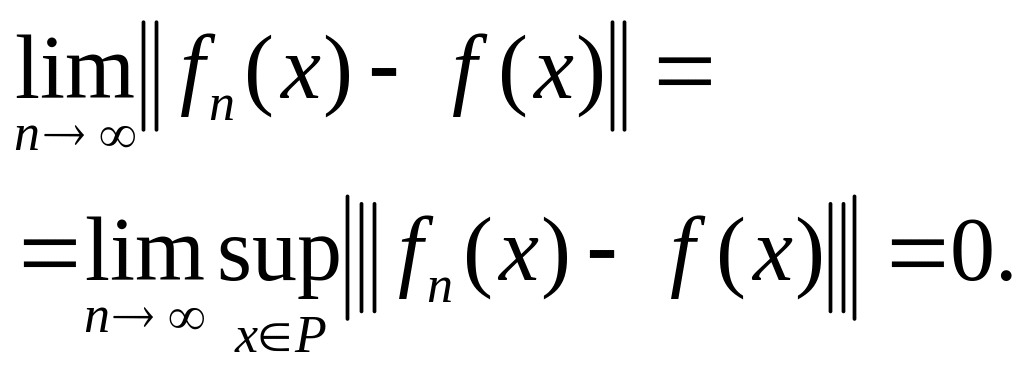
Пишут .

О₇:Функ-й р.(2) сх-йся к сумме S(x) н-ся равном-но сх-йся на мн-ве Р к S(x), если

Р ассм-м 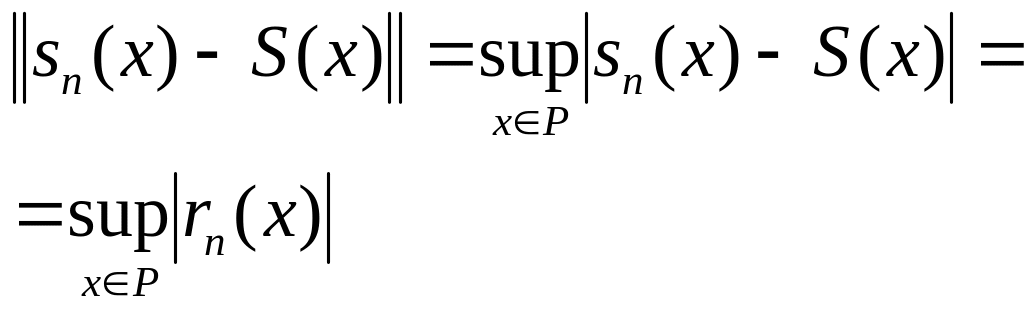, где r_n(x) – остаток. Т.о. функц.р. сх-ся на Р равномерно  когда , .

Получили необх. и дост. признак равномерной сх-сти функц. ряда.

Т₁: (пр-к Вейерштрасса). Если ,каждый член функ-го р.(2) по модулю не превышает соотв-го члена сх-ся числового р.(5) с полож-ми членами ( ), то функ-ый р.(2) на мн-ве Р сх-ся равномерно и абсол-но.(без д-ва)

1 9. Степ-ые ряды в компл. Области.

О₁: Ряд вида 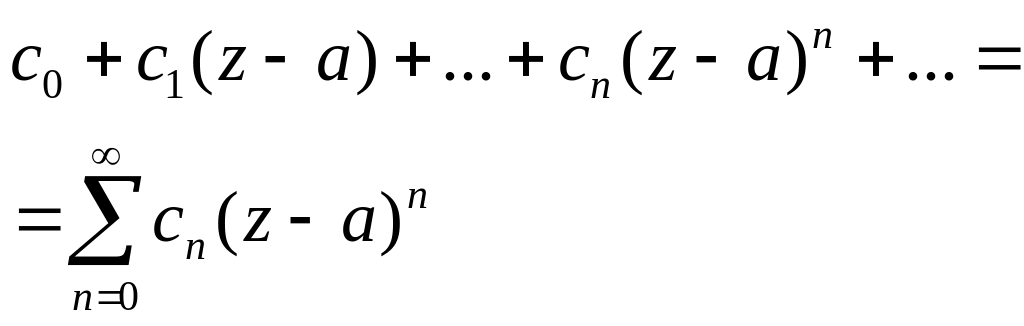(1) наз-ся степ-ым рядом. - постоян. комплекс. числа. Заменой z-a=w р. (1) сводится к р. (2), т.е. к ряду с центром в т. w =0.

Всякий степ. р. (1) сх-ся в центре ряда, т. е. в z=a. Возможны 3 случая:

1). (1) сх-ся только в центре ряда;

2). (1) сх-ся при конечных z;

3) при некот. z р.(1) сх-ся, при других рассх-ся.

Для любого степ. ряда, имеющего как точки сх-сти, так и точки рассх-сти, круг, внутри к-го ряд абс-но сх-ся, а вне - расх-ся. Этот круг наз-ся кругом сх-сти, а его радиус r – радиусом сх-сти. Если ряд сх-ся только в центре, то полагаем r=0; если сх-ся при всех z, то r=∞. На границе |z|=r ряд нужно исследовать дополн-но.

Вычисление радиуса сх-сти (1) сводится к отысканию радиуса абс. сх-сти ряда , к-ый яв-ся степ.рядом с действ. членами.

Т₁: (Абеля). Если степ-й р.(3) сх-ся в т. z₀≠0, то он сх-ся абсол-но при всех (в круге с центром в т. О радиуса ).

Д-во: По усл. числовой ряд (4) сх-ся и по необ-му приз-ку сх-ти . Значит сх-ся и, след-но, огран-на, т.е. такая, что справ-во <M. Оценим теперь общий член р.(3): (5)

Пусть число z фиксировано, причем |z|<|z₀|. Тогда . Из (5) получаем при всех n. Это означает, что члены ряда не превосходят соот-щих членов сх-щейся геометр. прогрессии , т.е. ряд (1) сх-ся абсолютно.

Сл-е1:Если р.(3) расх-ся в т. z_0, то он расх-ся при всех .

Дейст-но, если бы р.(3) сх-ся в к.- л. т.z при , то по Т. Абеля он сх-ся бы и в т. z₀.

Сл-е 2: Для всякого степ.р. сущ-ет число R такое, что внутри круга |z-a|<R ряд сх-ся, а вне круга расх-ся.