12. Опред-ный интеграл. Интегри-руемость непрерывной функции. Формула Ньютона-Лейбниц

Пусть на [а, b] задана ф-ция f (х). Разобьем [а, b] на n произв-ных частей точками деления а=x₀<x₁<...<x_n =b. Эту сис-му точек x_i (i = ) назовем разбиением Т сегмента [а, b]. Δх_i=х_i–x_i-1,

Число λ зависит только от разбиения Т, т.е. λ=λ(Т). Выберем произв-ную точку (i = ) и составим сумму

О1. Сумма наз-ся интегральной суммой или суммой Римана для функции f(х) на [а, b].

О2. Число J наз-ся пределом интег-ральных сумм σ, если ε>0 такое, что для любого разбиения Т сегмента [а,b], удовлет-щего условию λ(Т)<δ, и для любого выбора точек ,выполн-ся нерав-во . Пишут

О3. Если , то этот предел наз-ся определенным инте-гралом ф-ции f(x) на [а,b]. Пишут , а - нижний, в - верхний предел интегрирования.

О4. Ф-ция f(х), для к-ой , наз-ся интегр-мой на[а,b].

Т1. Ф-ция, интегрируемая на [а,b],-ограничена на [а,b].

Д-во. Допустим противное, т.е. пусть f(х) не ограни­чена на [а,b]. Т - произ-вольное разбиение [а,b]. Т.к. f(х) не ог­раничена на [а,b], то она не ограничена по крайней мере на одном [х_к-1,х_к]. Выбрав точку подходящим образом, слагаемое f( )Δх_к можно сделать как угодно большим по абсолютной величине. Но тогда суммы σ при λ(Т)→0 не могут иметь конечного предела. ЧТД

-ние определенного интеграла.

Т1. Для интегрируемости ограни-ченной ф-ции на некотором отрезке необх. и дост., чтобы выполнялось условие (S-верхняя интегральная сумма Дарбу, s-нижняя)

Некот. классы интегрир-мых ф-ций.

Т1. Если ф-ция f(х) непрерывна на [а, b], то она интег­рируема на [а,b]

-Ние первообразной. Формула Ньютона-Лейбница (н.-л.)

Т1. Если ф-ция f(x) непрер-на на [а, b], то f(x) на [a,b] имеет первообразную.

Д-во: Одной из первообразных является

, т.к. G(x)=f(x), x [а,b]. ЧТД.

Т2. (Основная теорема интеграль-ного исчисления). Пусть ф-ция f(х)непрерывна на [а,b],F(x)- какая-нибудь из ее первооб­разных на [а,b]. Тогда

Эта ф-ла наз-ся ф-лой Н.-Л.. Она устанавлива­ет связь между опред-ным и неопределенным интегралами.

Д-во: Ф-ция - одна из первообразных для f(х) на [а,b]. Произвольная первообразная F(x)=G(x)+С, x [а,b].

.

Положив x = a, находим F(a)=С. При х=b имеем , т.е.

. ЧТД.

Пишут:

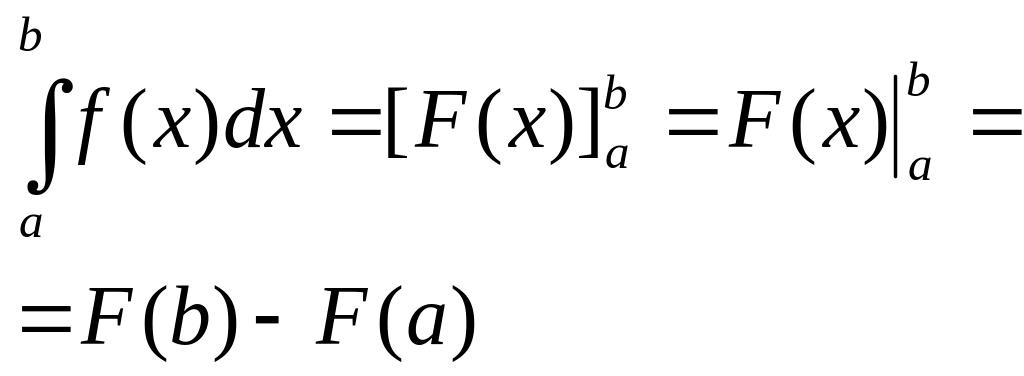
14. Вычисление s в декартовых и полярных координатах,

I. Пусть ф-ция у = f(x) непрерывна и неотриц-на на [а, в]. Рассм-м криволинейную трапецию (Р), ограниченную кривой у=f(x) и прямыми у=0, х=а, х=в. Т-любое разбиение [а,в] на (i = ).

Составим суммы Дарбу ,

Сумма s- площадь ступенчатого многоугольника (А), -гося в (Р), S - площадь ступенчатого много-угольника (В), содержащего (Р).

Т.к. f(x) непрерывна, то она интегри-руема на [а, в]. Значит, S–s→0 при λ→0 и фигура (Р) квадрируема, а ее площадь Р =-а общему пределу S и s, т.е.

II. Пусть кривая задана полярным ур-нием r = g(φ), g(φ)≥0 непрерывна на [α, β]. Фигура, ограниченная кривой r = g(φ) и двумя радиусами - векторами φ=α, φ=β наз-ся сектором (Р). Разобьем [α, β] на n произв-ных частей точками деления α=φ₀<φ₁<…< φ_n=β и проведем соотв-щие радиусы- векторы. Сектор (Р) разбив-ся на n частичных секторов. Рассмотрим i-ый сектор. Обозначим φ_i–φ_i-1=Δ φ_i, Круговые секторы с углом Δ φ_i и радиусами m_i и M_i имеют соотв-но площади .

Расс-м две фигуры (Q) и (R), составленные из круговых секторов с радиусами m_i M_i (i = ) cоотв-но. Их площади

Фигура (Q) -ся в (Р), фигура (R) (Р). Суммы Q и R яв-ся сум-мами Дарбу для ф-ции на [α, β] . Эта ф-ция непрерывна и потому интегрируема на [α, β]. Значит,

R-Q→0 при т.е. (Р) квадрируема и