2 3. О.Д.У. Первого порядка. Ур-я с разд-ся пер-ми. Линейные д.У.

О.д.у. первого порядка

О.д.у. наз-ся ур-е, связывающее незав-ю пер-ю, неизв-ю ф-цию этой пер-ой и ее производные разл-х по-рядков. Порядком д.у. наз-ся наивыс-ший порядок входящих в него произ-водных. Общий вид обык-го д.у. n-го порядка: , где F нек-я функция (n+2) пер-х.

О. Всякая фу-ция у=у(х), при подстановке к-ой о.д.у. обращается в тождество, наз-ся решением этого д.у.

Всякое о.д.у. имеет ∞-ное мн-во реше-ний. Для о.д.у. п-го порядка сущ-ет реш-е, содержащее п произв-х пост-х. Такое реш-е наз-ся общим решением. Придавая произвольным пост-м общего реш-я различные числовые значения, будем получать частные реш-ия д.у. Частное реш-ие д.у. не содержит произв-х пост-х.

Операцию нахождения решений д.у. наз-ют интегрированием д.у. Взятие интеграла будем называть квадрату-рой. Общее реш-ие д.у., особенно если оно записано в неявной форме, часто наз-ют общим интегралом.График решения д.у. наз-ют интегральной кривой этого д.у.

Пусть д.у. первого порядка задано в виде , где определена в нек-ой области G. Это ур-е ставит в соот-е каждой точке (x,y)G опред-е значение у'. Иначе говоря, ур-е (1) задает в каждой точке области G нек-ое направление, совпадающее с направлением каса-тельной к интегральной кривой, прохо-дящей через эту точку. Совокупность этих направлений наз-ся полем направлений ур-я (1). Для наглядного изображения поля направлений в каждой точке области G проводят отрезок с угловым коэф-ом у'.

При построении поля направлений удобно рассм-ть геом-е места точек, в к-ых у' имеет пост-е значение. Мн-ва таких т-к наз-ют изоклинами.

Начальные условия

Пусть дано ур-е первого пор-ка . Ее общее реш-е содержит одну произвольную пост-ую: . Часто треб-ся найти то частное реш-е, к-е при х=х₀ принимает знач-е у=у₀. Эти условия наз-ся нач-ми условиями. Чтобы удовлетворить нач-м условиям, нужно определить соот-ующее знач-е пост-ой . Нач-е усл-я записывают: или .

Частное реш-е, удовл-ее нач. усл-ям, наз. реш-ем с нач. усл-ми. Ему соответствует интегральна кривая, проходящая через точку .

Общее реш-е д.у. n-го порядка содержит n произвольных пост-ых: . Их можно найти, если иметь n условий , ,…, . Соот-вующие знач-я пост-ых нах-им из системы

Задачу нах-ия реш-ия у=у(х) д.у. , удовл-го нач. усл-ям , наз-ют задачей Коши (анал-но и для д.у. порядка k, k>1).

Ур-ния с раздел-мися переменными

Д.У.-ми с разд-ся пер-ми наз-ся ур-я вида (1).

Предполагая g(x) и h(y) непр-ми в нек-ой области G и , произведем разделение пер-х. Т.к. ф-ции g(x) и h(y) непрерывны в G, то они имеют первообр-е, отлич-ся только на пост-ю.

(2).

Соотн-е (2) явл-ся общ. реш-ем ур-я (1). Общее реш-е нах-ся двумя квадра-турами. Оно получено при условии в G. Если при нек-ом будет h(y)=0, то непосредст-но из (1) видим, что — тоже реш-е ур-я (1), не содержащееся в (2). Если нужно найти реш-е ур-я (1) с нач-ми усл-ми , то, вместо нах-я соот-го значения пост-ой с в (2), можно сразу взять интегралы от х₀ до х и от у₀ до у. Получим нужное частное решение.

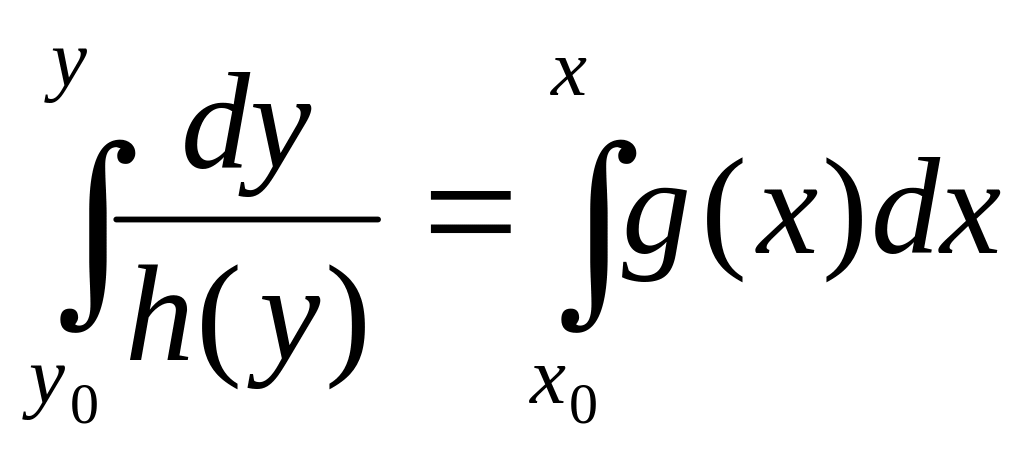
Линейные ур-ния первого порядка

Д.у. наз-ся лин-м, если его правая часть явл-ся лин-ой ф-ей отн-но у. Лин-е ур-е имеет вид (1), где и — задан. непрер-е ф-ции от х. Если , то ур-е (1) наз-ся лин-ым однородным, иначе — неоднор-м.

Метод вариации постоянной

При решении ур-я (1) этим м-дом сначала интегрируется соот-е однородное ур-е . Это ур-е с разд-ся пер-ми.

; ; ; (2) .

При разделении пер-х потеряли реш-е у=0, включим его в (2), полагая с=0.

Переходим к реш-ю неодн-го ур-я, т.е. ур-я (1). Заменим в (2) пост-ю с ф-цией с(х) и подберем с(х) так, чтобы удовл-сь ур-е (1). Итак, подставим (3) в (1).

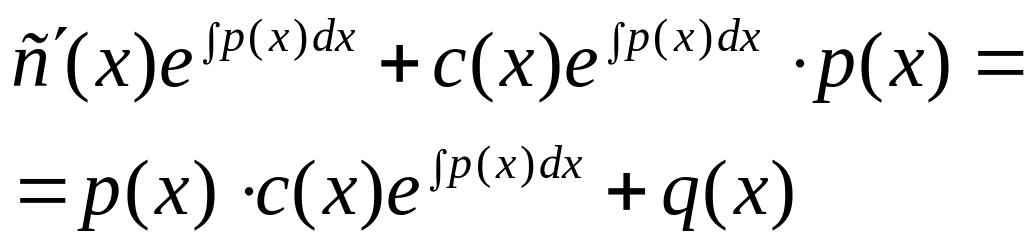. Отсюда , т.е. . Подставив найд-ую ф-цию с(х) в (3), получим общ. реш-е лин-го неод-го ур.

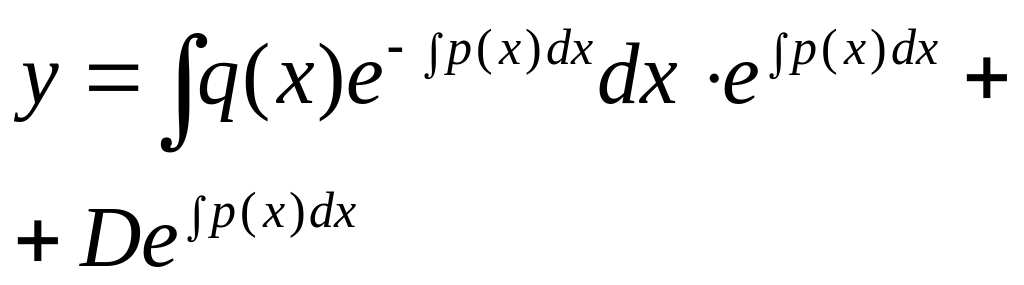(4)

Здесь 2-ое слагаемое — общее реш-е соотв-го однор-го ур-я, а первое — частное реш-е неодн-го (D=0). Так что общее реш-е лин-го неодн-го ур-я (1) явл-ся суммой какого-либо частного решения этого ур-я и общего реш-я соотв-го однор-го ур-я.