
- •1 . Мощность мн-ва. Счётность мн-ва рациональных чисел. Несчётность мн-ва дей-х чисел.
- •2. Предел и непрерывность функций в точке. Св-ва непрерывных функций на отрезке.
- •3 . Предел числовой послед-ности. Теорема Больцано.
- •4. Определение и существование степени с иррациональным показателем.
- •5. Степенная функция с иррациональным показателем. Степень в комплексной области.
- •7. Разложение функций sin X и cos X в степенной ряд. Синус и косинус в комплексной области
- •8. Дифференцируемые функции. Правила дифференцирования
- •9 . Теорема Лагранжа. Условия монотонности и выпуклости функции на промежутке
- •1 0. Экстремумы и точки перегиба
- •12. Опред-ный интеграл. Интегри-руемость непрерывной функции. Формула Ньютона-Лейбниц
- •-Ние первообразной. Формула Ньютона-Лейбница (н.-л.)
- •14. Вычисление s в декартовых и полярных координатах,
- •1 6. Числовые ряды. Признаки сходимости: Даламбера и Коши.
- •17. Абсолютно и условно сх-ся ряды.
- •18.Функциональные послед-ти и ряды.
- •1 9. Степ-ые ряды в компл. Области.
- •20. Формула и ряд Тейлора.
- •2 1. Метрические пространства. Полные метрич. Пр-тва
- •2 3. О.Д.У. Первого порядка. Ур-я с разд-ся пер-ми. Линейные д.У.
- •2 4. Линейные д.У. С пост-ми к-нтами
- •25. Производная ф-ции компл.Пер. Условия диф-ти. Понятие аналитич. Ф-ции
2 4. Линейные д.У. С пост-ми к-нтами
Рассм-м
неодн-е лин-е ур-е
![]() ,
(1)
,
(1)
![]() —
пост-е д.ч. Будем искать реш-я в виде
—
пост-е д.ч. Будем искать реш-я в виде
![]() .
Так
как
.
Так
как
![]() ,
то,
подставив и разделив
на
,
то,
подставив и разделив
на
![]() ,
получим
,
получим
![]() .
(2)
-
хар-е ур-е для ур-я (1),
оно имеет
n
корней.
.
(2)
-
хар-е ур-е для ур-я (1),
оно имеет
n
корней.
Случай
1.
Корни
хар-го ур-я (2) действ-ны и разл-ны,
![]() .
Получаем n
частных реш-ий.
.
Получаем n
частных реш-ий.
![]() .
Покажем,
что они составляют фундаментальную
систему ур-я (1). составим определитель
Вронского
.
Покажем,
что они составляют фундаментальную
систему ур-я (1). составим определитель
Вронского
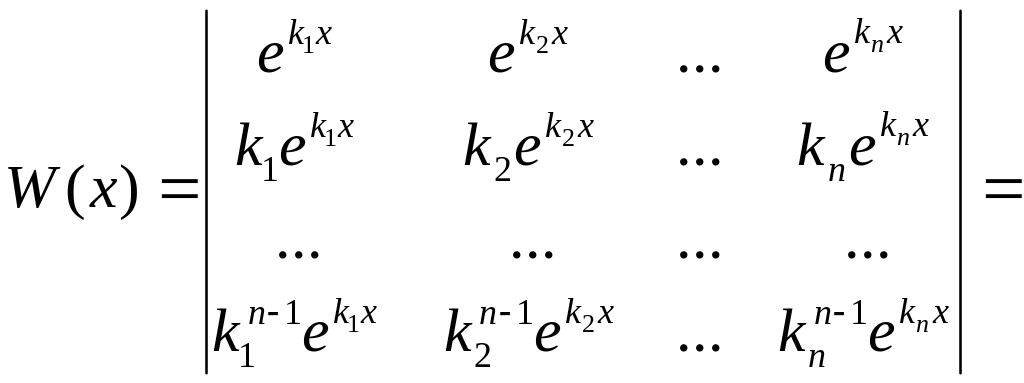
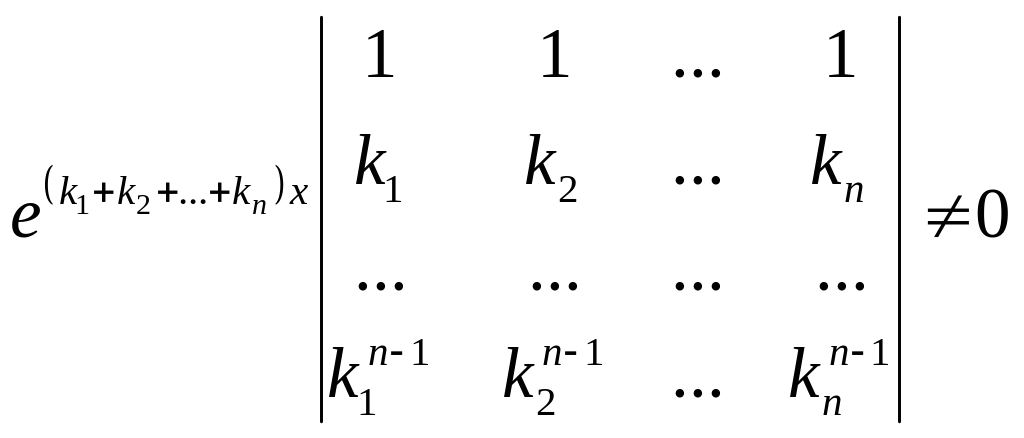 .
.
(Последний
опред-ль есть опред-ль Вандермонда,
к-ый
![]() при
при
![]() ).
Тогда общее реш-е ур-я (1)
).
Тогда общее реш-е ур-я (1)
![]() (3).
(3).
Случай 2. Если среди разл-ых корней ур-я (2) им-ся компл-ные, то повторяя приведенные рассуждения получим общ. реш-ие ур-я (1) снова в форме (3), но тогда у будет компл-ной ф-цией действ-й перем-ой х. Чтобы избежать использование комплексных выражений поступают след образом:
Если
имеется компл-ый корень
![]() ,
то сопряженное число
,
то сопряженное число
![]() тоже явл-ся корнем ур-я (2). Паре компл.
сопряженных корней
тоже явл-ся корнем ур-я (2). Паре компл.
сопряженных корней
![]() соотв-ет пара действ-ых частных реш-ий:
соотв-ет пара действ-ых частных реш-ий:
![]() ,
,![]() .
.
Случай
3. Среди
корней ур-я (2) им-ся кратные. Пусть k
– действ-ый корень кратности r.
Этим r
одинаковым корням соотв-ют частные
решения
![]() .
Если корень кратности r
явл-ся компл-ым
.
Если корень кратности r
явл-ся компл-ым
![]() ,
то
,
то
![]() тоже корень, той же кратности. Этим 2r
корням соотв-ют 2r
частных решений вида
тоже корень, той же кратности. Этим 2r
корням соотв-ют 2r
частных решений вида![]() ,
,
![]() ,…,
,…,![]() ;
;
![]() ,
,
![]() ,…,
,…,![]() .
.
Неоднор-ные лин-ые ур-ния с пост-ми коэф-ми. Метод неопред-х коэффициентов
Расс-м ур-ние
![]() ,
(1),
где
,
(1),
где
![]() —
постоянные действительные числа.
—
постоянные действительные числа.
Т
.к.ур-ние
(1) яв-ся
лин-ым,
то его общее реш-ие
можем искать
методом вариации постоянных. Ур-ние
(1) можно интегрировать и другим методом,
если ф-ция
v(x)
имеет
спец-ный
вид. Если известно общее реш-ие
соотв-щего
однор-го
ур-ния
![]() ,
то для нахождения общего реш-ия
ур-ния
(1) достаточно найти к-нибудь част.
решение уравнения (1). Если v(x)
имеет
специальный вид, то частное решение
можно найти методом неоднор-х
коэффициентов.
,
то для нахождения общего реш-ия
ур-ния
(1) достаточно найти к-нибудь част.
решение уравнения (1). Если v(x)
имеет
специальный вид, то частное решение
можно найти методом неоднор-х
коэффициентов.
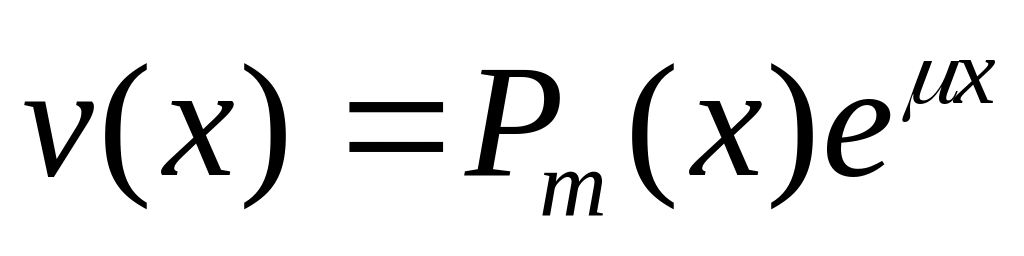 ,
где
,
где
 —
действ-ное
число,
—
действ-ное
число,
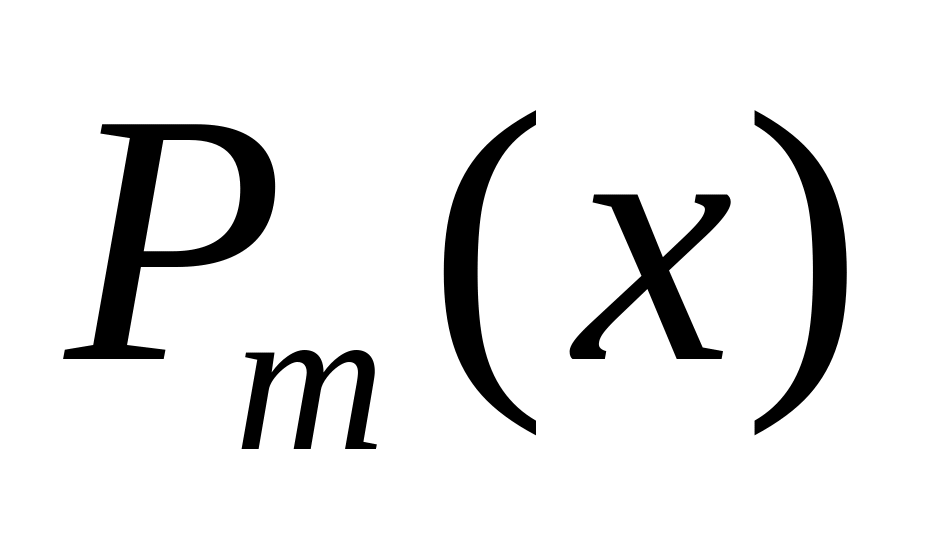 — многочлен степени m.
— многочлен степени m.Пусть не яв-ся корнем характер-кого ур-ния. Можно показать, что сущ-ет частное решение уравнения (1) вида
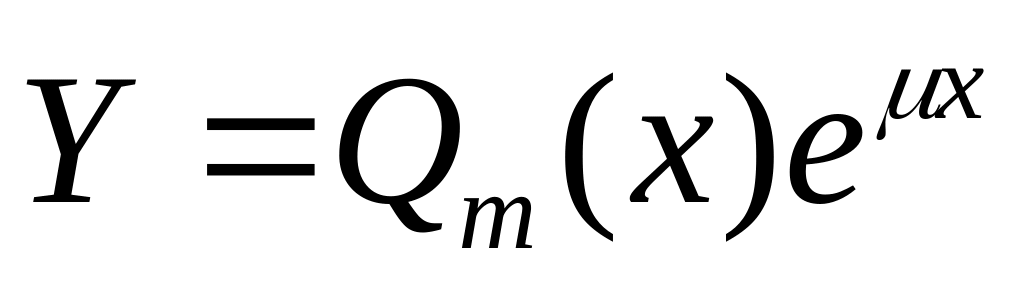 ,
где
Qm(х)
— многочлен степени
m
.
,
где
Qm(х)
— многочлен степени
m
.
Записав Qm(x) с неопред-ми коэф-ми, подставим Y в ур-ние (1) и найдем эти коэффициенты.
Если — корень характер-кого ур-ния кратности r, тогда част. реш-ие ищем в виде
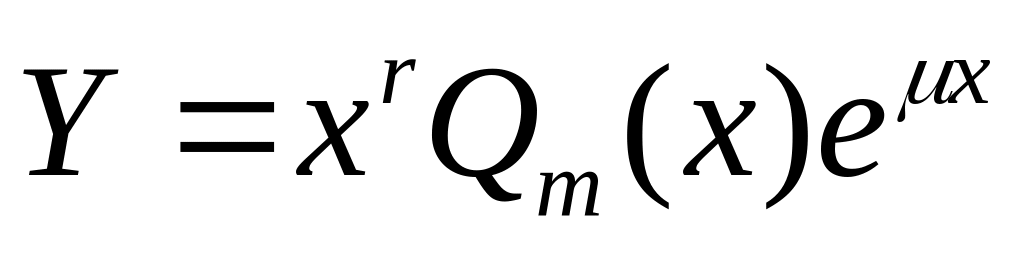 .
.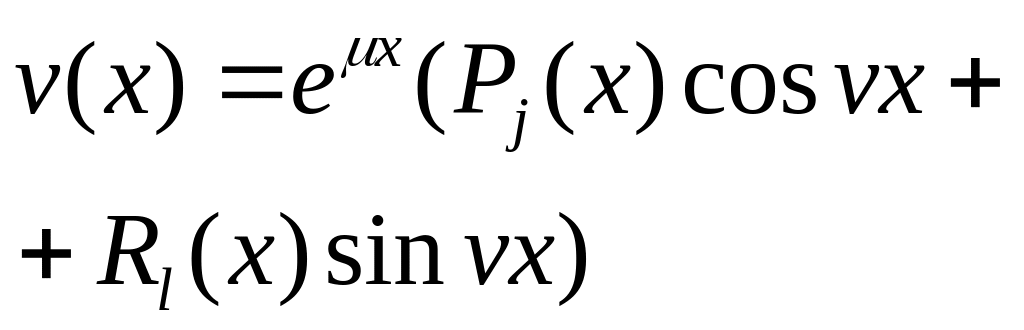 ,
где
и
v
—действ-ные
числа,
Pj(х)
и
Rl(x)
–
мн-ны
степени
j
и
l
соотв-но.
,
где
и
v
—действ-ные
числа,
Pj(х)
и
Rl(x)
–
мн-ны
степени
j
и
l
соотв-но.
Обозн-м
m=max{j,l},
k=μ+iv.
Если
k
— корень характер-кого
ур-ния
кратности r,
то
част.
реш-ие
![]() ,
где
Qm(х)
и Sm(х)
–
мн-ны
степени m.
,
где
Qm(х)
и Sm(х)
–
мн-ны
степени m.
III.
![]() ,
где каждое слагаемое имеет тип II.
Интегрируем m
неоднор-х
ур-ний
,
где каждое слагаемое имеет тип II.
Интегрируем m
неоднор-х
ур-ний
![]() ,
(
,
(![]() ).
Для каждого из них находим част.
решение Yi(х).
Тогда
).
Для каждого из них находим част.
решение Yi(х).
Тогда
![]() —
част-ое
реш-е
исход-го
ур-ния.
—
част-ое
реш-е
исход-го
ур-ния.
25. Производная ф-ции компл.Пер. Условия диф-ти. Понятие аналитич. Ф-ции
П усть
ф-ция
усть
ф-ция
![]() определена
и однозначна на мн-ве Е,
z0
-
предельная точка мн-ва Е,
определена
и однозначна на мн-ве Е,
z0
-
предельная точка мн-ва Е,
![]() .
Пусть
.
Пусть
![]() ,
,
![]() -
приращением ф-ции в точке z0.
-
приращением ф-ции в точке z0.
О1.
Если
сущ-ет
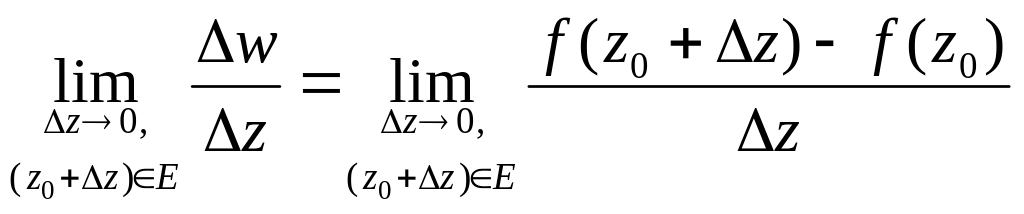 ,
то этот предел наз-ся производной
,
то этот предел наз-ся производной
![]() по мн-ву Е в т.
по мн-ву Е в т.
![]() и обознач-ся
и обознач-ся
![]() или
или
![]() ,
а ф-ия
f(z)
наз-ся диффер-руемой по мн-ву E
в т. z0.
,
а ф-ия
f(z)
наз-ся диффер-руемой по мн-ву E
в т. z0.
Пусть
ф-я w=f(z)
диф-ма в т.
z0,
тогда
![]() ,
причем
,
причем
![]() .
Тогда
.
Тогда
![]() (1):
1-й член линеен отн-но ∆z,
а 2-й →0 при ∆z→0.
(1):
1-й член линеен отн-но ∆z,
а 2-й →0 при ∆z→0.
Обратно,
если приращение ф-ии w=f(z)
в т.z0,
м. представить в виде ∆w=A∆z+ε(z0,∆z)∆z
(1), где
![]() при ∆z→0,
следует, что ф-ия
им. произв-ю в
т.z0,
т.к.
при ∆z→0,
следует, что ф-ия
им. произв-ю в
т.z0,
т.к.
![]() .
A=const.
Из (1) =>, если
дифф-ма
в т.z0,
то она непрер-на на ней.
.
A=const.
Из (1) =>, если
дифф-ма
в т.z0,
то она непрер-на на ней.
О2.
Линейная
отн-но
![]() часть
приращения функции
часть
приращения функции
![]() ,
т.е. произведение
,
т.е. произведение
![]() наз-ся
диффер-лом ф-ции в
точке и
обозн-ся
dw
или
df(z0).
Приращение
аргумента
наз-ся
дифф-лом
аргумента и обозн-ют dz.
Т.о.,
наз-ся
диффер-лом ф-ции в
точке и
обозн-ся
dw
или
df(z0).
Приращение
аргумента
наз-ся
дифф-лом
аргумента и обозн-ют dz.
Т.о.,
![]() .
.
Из опр-ия производной и св-в пределов ф.к.п. =>, что правила дифф-ия, распр-ся и на ф.к.п.
![]() с=const;
с=const;
![]()
![]()
![]()
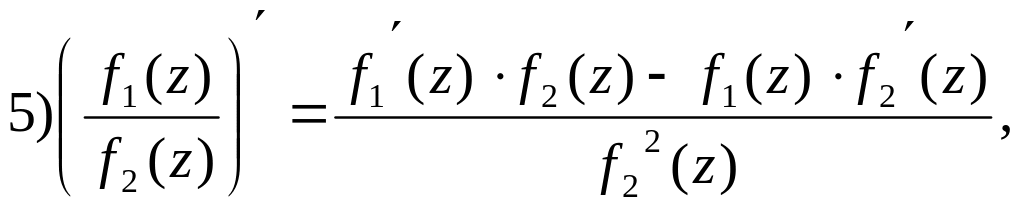
![]()
![]()
F – мн-во значений ф-ий f(z).
7)
если
![]() - обратная ф-ия, то
- обратная ф-ия, то
![]()
Требование
сущ-я предела отн-но
![]() незав-мо от сп-ба стремления ∆z→0
связ-ет действ. и мним. части ф.к.п.
особыми усл-ми.
незав-мо от сп-ба стремления ∆z→0
связ-ет действ. и мним. части ф.к.п.
особыми усл-ми.
Т.
Для
того,
чтобы
ф-ия
![]() в
т. z0=x0+iy0
была
диф-емой,
необх. и дост-но,
чтобы:
в
т. z0=x0+iy0
была
диф-емой,
необх. и дост-но,
чтобы:
1 ) ее д.часть и(х,у) и мнимая v(x,y) были диф-емыми ф-циями в т.(х0,у0),
2)
в
т.(х0,у0)
вып-ись усл-ия Коши-Римана (Даламбера-Эйлера):
![]()
![]() .
.
Тогда
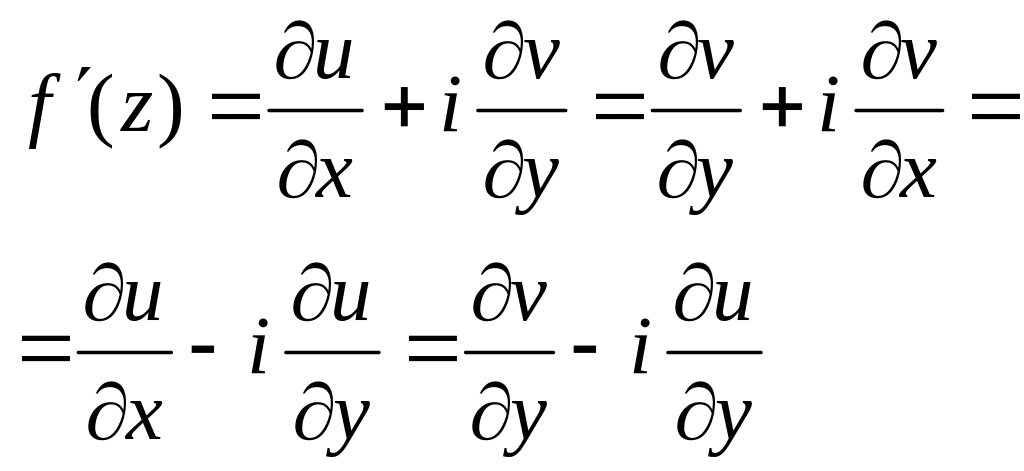
Д-во:
Необх.
Пусть
ф-ия
диф-ма
в т.z0,
т.е.
вып-ся усл-е ∆w=f′(z0)∆z+ε(z0,∆z)∆z
(1).
Положим
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Здесь
.
Здесь
![]() ,
,
![]() при
при
![]() ,
,
![]() .
Отделим в (1)
действ. и мним. части:
.
Отделим в (1)
действ. и мним. части:
![]() ,
,
![]() .
.
Из этих формул следует: 1) ф-ии и(х,у) и v(x,y) диф-мы как ф-ии 2-х действ-х переем-х в т.(х0,у0);
2)![]() в
т.(х0,у0),
откуда
вытекает справедливость
условий К-Р.
в
т.(х0,у0),
откуда
вытекает справедливость
условий К-Р.
б
)
Дост.
Пусть
ф-ии
и(х,у)
и
v(x,y)
диф-мы в т.(х0,у0)
и
выполнены усл-я К-Р:
![]() ,
,
![]() ,
где
,
где
![]() при
,
.
Кроме того
при
,
.
Кроме того
![]() .
Тогда
∆w=∆u+i∆v=a(∆x+i∆y)+ib(∆x+i∆y)+(α1+iβ1)∆x+(α2+iβ2)∆y=(a+ib)∆z+
+((α1+iβ1)∆x/∆z+(α2+iβ2)∆y/∆z)∆z=A∆z+ε∆z.
(2)
.
Тогда
∆w=∆u+i∆v=a(∆x+i∆y)+ib(∆x+i∆y)+(α1+iβ1)∆x+(α2+iβ2)∆y=(a+ib)∆z+
+((α1+iβ1)∆x/∆z+(α2+iβ2)∆y/∆z)∆z=A∆z+ε∆z.
(2)
Т.к.
![]()
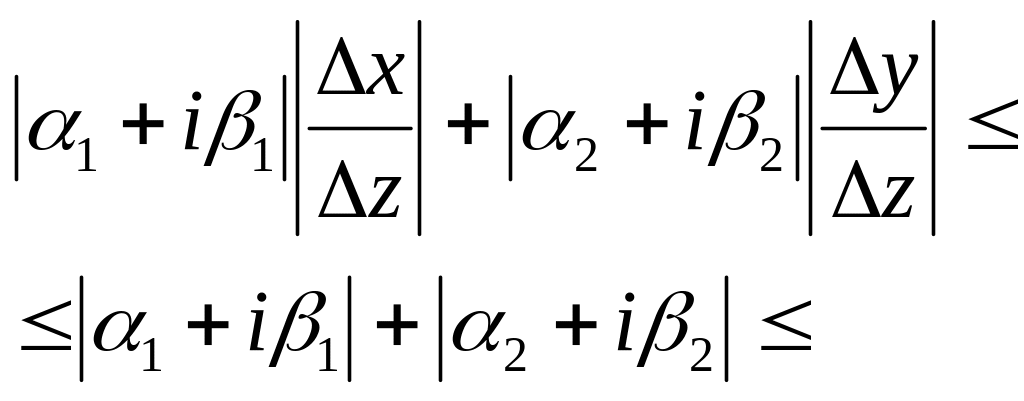
![]() ,
,
то
![]() при
при
![]() .
Из (2) следует, что ф-ия
диф-ма в т.z0.
Причем,
.
Из (2) следует, что ф-ия
диф-ма в т.z0.
Причем,
![]()
![]() .
•
.
•
