1 6. Числовые ряды. Признаки сходимости: Даламбера и Коши.

О₁: Символ u₁+u₂+…+u_n+… (1) или наз-ся числ. рядом, u₁,u₂,…u_n,_… - его члены, а u_n – общий член р. (1). s_n=u₁+…+u_n,… наз-ся n-ой частичной суммой р. (1).

О₂: Ряд (1) наз-ся сходящимся, если {}-cть его частичных сумм {s_n} имеет конечный предел. Ряд наз-ся расх-ся, если посл-ть {s_n} не имеет конеч.предела.

О₃: Суммой S сх-ся ряда наз-ся предел {}-cти его частичных сумм, т.е. .

В этом случае пишут S= .

Согласно О₂ вопрос о сходимости р. (1) сводится к вопросу о -нии конеч. lim-a для {s_n}. Обратно, для {a_n} вопрос о -нии для нее конеч. lim-a можно свести к вопросу о сх-сти ряда a₁+(a₂-a₁)+…+(a_n–a_n-1)+…. Частичные суммы этого р. яв-ся членами {a_n}.

Расх-ся р. можно : на 2 категории:

1). собственно расх-ся р., у к-ых {s_n} имеет пределом ∞(+∞,-∞). Пишут

2). р., у к-ых {s_n} ни имеет ни конеч., ни ∞-го lim-а.

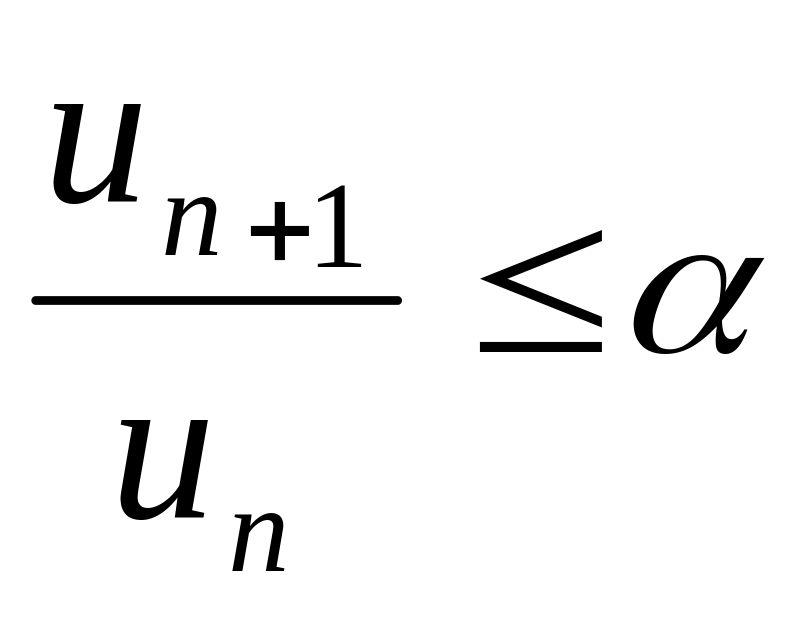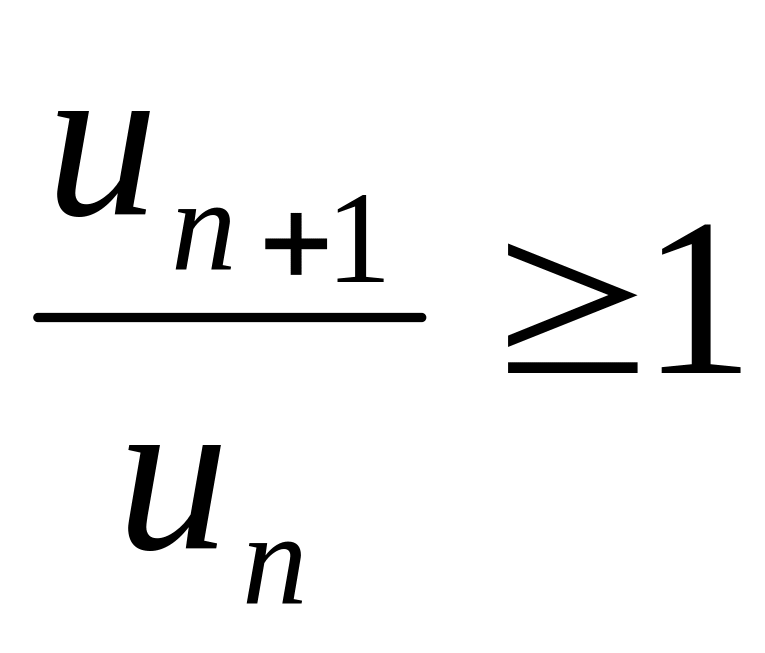Т₁: (пр. Даламбера). Если для р. (1) с «+»-ми членами, начиная с некот. номера, вып-ся нер-во (α- const и α <1), то р. (1) сх-ся. Если же, начиная с некот. номера, , то р. (1) расх-ся.

Д-во: Т.к. конеч. число первых членов не влияет на сх-ть или расх-ть ряда, то без ограничения общности можно считать, что 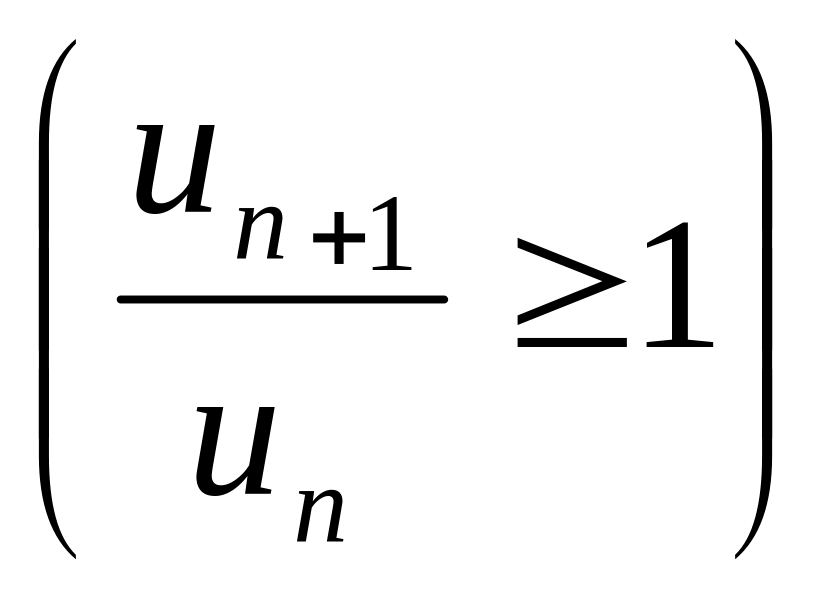вып-ся для всех n=1,2,….

1) ] <1 , т.е. Перемножим эти нер-ва Так что все члены р. (1) не превышают соотв-х членов геометр. р. с «+»-ми чле-нами α<1, кот. сх-ся. Тогда по приз-наку сравнения сх-ся и р. (1)-сх-ся.

2) ] . След-но, ≥ , т.е. общий член р. (1) не → к 0 при n→∞, и поэтому ряд расх-ся. ЧТД.

Т₂: (Пред-я форма пр-ка Д-ра). Если для ряда (1) с «+»-ми членами ,то при q<1 р. (1) сх-ся, при q>1 р. (1) расх-ся.

Д -во: 1)] и α- произв-е число q<α<1. Тогда начиная с некот-го номера будет и по Т₁ р. сх-ся.

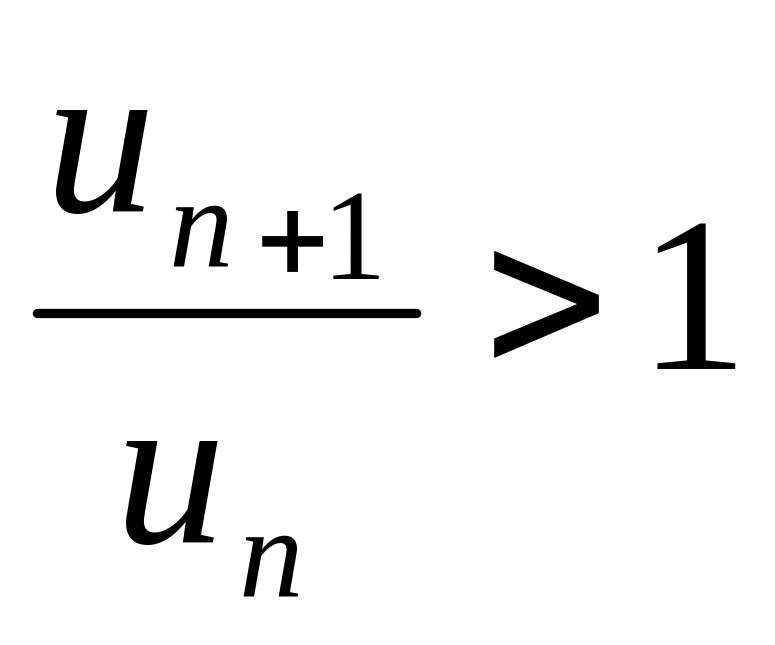2) ] , начиная с некот-го номера будет , по Т₁ ряд расх-ся. ЧТД.

Зам-е: Если , то пр-к Дал-ра не позволяет судить о поведении ряда.

Т₃: Если для ряда с «+»-ми членами (1) начиная с некот. номера вып-ся нер-во (α-const, α<1), то р.(1) сх-ся; если же, начиная с некот. номера, , то р.(1) расх-ся.

Д-во: Без ограничения общности снова считаем, что ( ) вып-ся .

1). . Отсюда . Значит все члены р.(1) не превышают соотв.-щих членов геом. прогрессии с «+»-ми членами α<1, кот. сх-ся. Тогда по признаку срав-ния сх-ся и р. (1)-сх-ся.

2) ] . Тогда , т.е. общий член р. (1) не → к 0 и поэтому ряд расх-ся. ЧТД.

Т₄: Если , то при q<1 р. сх-ся, при q>1- расх-ся.

Д-во: 1)] и α- произв-е число. q<α<1. Тогда и начиная с некот. номера будет и по Т₁ р. сх-ся.

2) ] , начиная с некоторого номера будет , по Т₁ ряд расх-ся. ЧТД.

Зам-е: Если , то пр-к Коши не позволяет судить о поведении ряда.

17. Абсолютно и условно сх-ся ряды.

Ряд (1) наз-ся абсолютно схо-дящимся, если сх-ся ряд (2).

Т₁: Если ряд сх-ся абс-но, то он сх-ся.

Д-во: ] (1) абс. сх-ся, т.е. сх-ся р. (2), тогда такой, что

(кр-й Коши). Тогда при тех же n и k. Согл-но кр-ю Коши р. (1) сх-ся.ЧТД.

Т₂: Сумма абс-но сх-ся ряда = разности м/у суммой ряда, составленного из одних «+»-ых членов исх-го ряда, и суммой ряда, сост-го из модулей «-»-ых членов.

Д-во:] р. (1) абс. сх-ся, s_n – его частич-я сумма, и -суммы абсол-х величин «+»-ых и «-»-ых членов из s_n, т.е. . Посл-ти { } и { } не убывают. По усл. р.(2) сх-ся, т.к. это р. с «+»-ми членами, то его частичные суммы ограничены сверху, а т.к. , то и { } и { } тоже огр-ны сверху и потому и . Получаем ■

Не всякий сх-ся ряд яв-ся абс-но сх-ся.

Для док-ва абс. сх-сти (1) к (2) следует применить признаки сх-сти, установленные для рядов с «+»-ми членами. В частности:

1. Если, начиная с некот. номера, 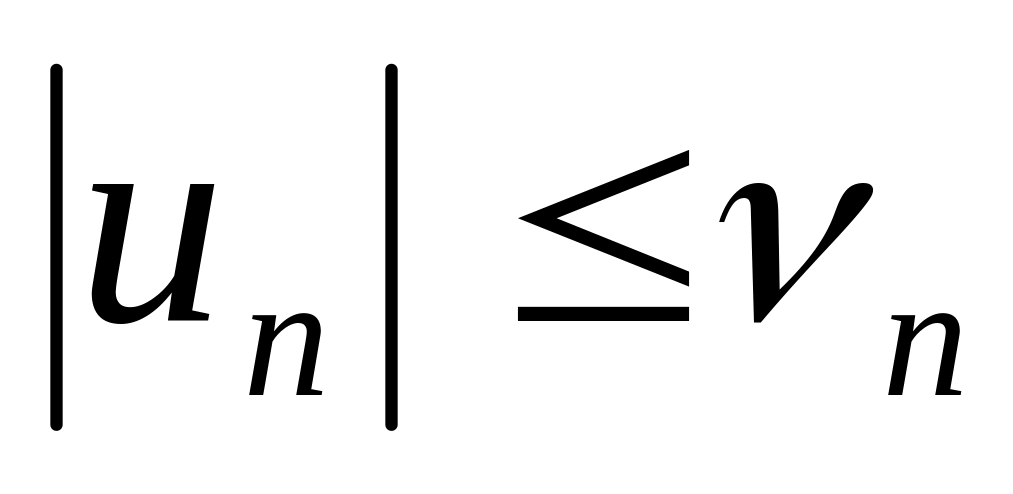, 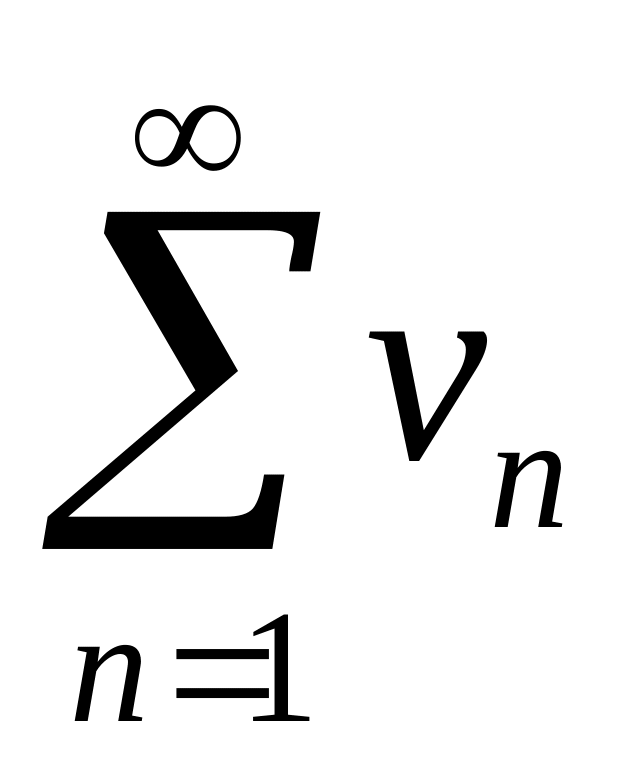-сх-ся ряд с «+»-ми членами, то (1)-абс.сх-ся.

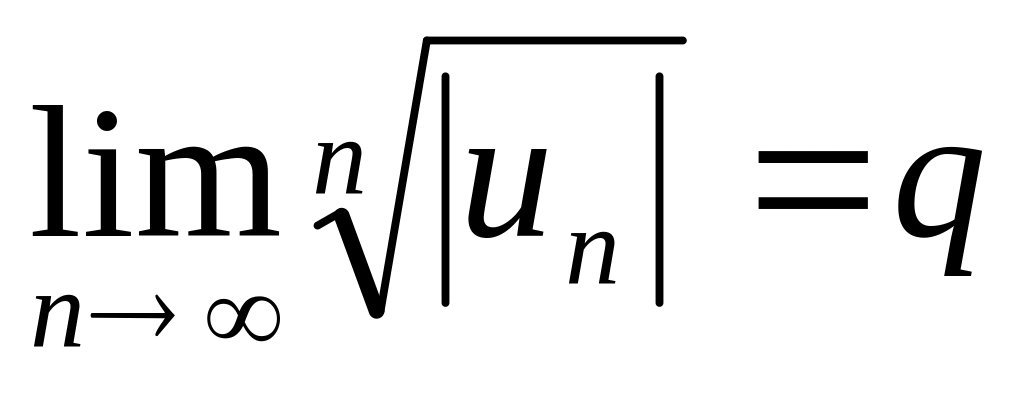2. Если конечный или ∞-ый , то при q<1 р.(1) сх-ся абсолютно, а при q>1 – расх-ся.

О₁: Если р. (1) сх-ся, а р. (2) расх-ся, то (1) наз-ся условно сх-ся.

Т₃: Если р. (1) усл. сх-ся, то ряд, состав-й из одних «+»-ых его членов, и ряд, сост-й из одних его отриц-х членов, расх-ся. Д-во: По усл. р. (1)-сх-ся, р. (2) –расх-ся. Ч/з s_n и обозначим частич. суммы этих рядов соотв-но.] и - суммы «+»-ых и абс-х величин «-»-ых членов в s_n. Тогда (3),

(4)

] хотя бы одна из величин или имеет конечный lim при n→∞. Т.к. s_n имеет lim при n→∞, то из (3) другая величина тоже имеет lim. Но тогда из (4) должна иметь lim при n→∞, а это противоречит расх-ти р. (2). Значит, и не могут иметь конеч-х lim при n→∞.■