§4. Сложное отношение.

4 .1. Определения и свойства.

Н апомним определение из векторной алгебры.

Опр. 4.1.1. Пусть точки A, B, C лежат на одной прямой. Число  называется простым отношением трех точек A, B, C, если AC;\s\up10( –( =  CB;\s\up10( –(. Это

равносильно тому, что точка C делит отрезок AB в отношении  >0, если C лежит между A и B. Если же C лежит за пределами отрезка AB , то будет  < 0. Пишем  = (AB,C) или  = (ABC). Хотя не существует операции деления одного вектора на другой, мы будем писать  = AC;\s\up10( –(/CB;\s\up10( –(, если AC;\s\up10( –(CB;\s\up10( –(.

Простое отношение трех точек сохраняется при параллельном проецировании. Но легко показать, что оно не сохраняется при центральном проецировании, т.е. оно не является проективным понятием. Поэтому в проективной геометрии вводится сложное отношение 4 точек.

Опр. 4.1.2. Сложным отношением четырех собственных точек A, B, C, D, лежащих на одной прямой, называется число

(ABCD) = ⁼ : ⁼ .

Будем также использовать такое обозначение сложного отношения: (AB, CD).

Из 4-х букв можно образовать 24 перестановки. Однако различных значений сложных отношений 4 заданных точек одной прямой может быть только шесть.

Теорема 4.1.1. При перестановке пар A,B и C,D значение сложного отношения сохраняется.

По определению (CD, AB) ^{= = =} (AB, CD).

Свойства сложных отношений. Пусть

1. (AB, CD) = . Тогда

2. (AB, DC) = 1/ ;

3. (AC, BD) = 1 –  ;

4. (AD, BC) = 1 ^– = ;

5. (AC, DB) = ;

6. (AD, CB) = ;

Докажем, например, свойство 2. По определению имеем:

(AB, DC) = = ^–1= = .

В каждом из пунктов 1 – 6 имеется по 4 равных значения для исходного значения сложного отношения. Возможны также частные случаи:

а) D = C  (AB, CC) = 1;

б) D = B  (AB, CB) = 0;

в) D = A  (AB, CA) =  .

Теорема 4.1.2. Пусть D – несобственная точка. Тогда (ABCD_) = – (AB,C).

(ABCD_) = . Вычисляем

(AB, D_) =Combin(AB, D) = Combin = Combin = Combin – 1 = – 1 

 (ABCD_) = = – (AB,C).

П

A, B ––;\s\up2(· · С, D

A, B  С, D

ара точек A, B (A  B) разбивает проективную прямуюна два отрезка. Пусть на прямой дана другая пара точек С, D. Точки С, D, принадлежащие одному отрезку называются неразделяющимися A, B (обозначаем A, B ––;\s\up2( · · С, D). Если же С, D принадлежат разным отрезкам, то они называются разделяющимися A, B (обозначаем A, B  С, D).

Если A, B ––;\s\up2(· · С, D , то (AB, CD) > 0. Если A, B  С, D , то (AB, CD) < 0.

Отношение разделенности (неразделенности) пар точек сохраняется при проективных преобразованиях.

4.2. Формулы сложных отношений.

1. Пусть точки A, B, C, D лежат на одной прямой a; ¯ и имеют в репере R координаты A(a₁, a₂), B(b₁, b₂), C(c₁, c₂), D(d₁, d₂). Требуется найти (ABCD).

Найдем (ABCD) в частном случае, когда R = {A_1 , A₂, E}. Тогда a₁/a₂ = a, b₁/b₂ = b, c₁/c₂ = c, d₁/d₂ = d, где a, b, c, d – обычные координаты на прямой. Поэтому

c₁ c₂

a₁ a₂

d₁ d₂

a₁ a₂

b₁ b₂

c₁ c₂

b₁ b₂

d₁ d₂

(ABCD) = (AC;\s\up10( –(/CB;\s\up10( –():(AD;\s\up10( –(/DB;\s\up10( –() = : = –––––– : –––––­– . (4.2.1)

Можно показать, что по этой формуле вычисляется (ABCD) и в произвольном репере на a; ¯ .

Лемма. Координаты точки Ma; ¯ в двух реперах R = {A₁, A₂, E} и R = {A₁, A₂ , E} на a; ¯ связаны между собой формулами

(4.2.2)

x₁ = c₁₁x₁ + c₁₂ x₂ ,

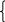
x₂ = c₂₁x₁ + c₂₂ x₂ .

Эта лемма доказывается дословно так же, как и аналогичная теорема для плоскости.

Теорема 4.2.1. Формула (4.2.1) имеет место в любом проективном репере.

Пусть точки A, B, C, D имеют в репере R = {A_1 , A₂, E} координаты A(a₁, a₂), B(b₁, b₂), C(c₁, c₂), D(d₁, d₂), а в репере R = {A₁, A₂ , E} – A(a₁, a₂ ), B(b₁ , b₂ ), C(c₁ , c₂ ), D(d ₁ , d ₂ ). Тогда (ABCD) вычисляется по формуле (4.2.1). Но, в соответствии с (4.2.2)

(4.2.3)

a₁ = c₁₁a₁ + c₁₂ a₂ ,

a₂ = c₂₁a₁ + c₂₂ a₂ .

И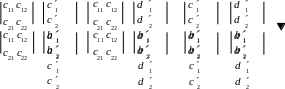 это же выполняется для координат других точек. Подставляя (4.2.3) в (4.2.1) получаем

· ·

(ABCD) = ––––––––––––––– : –––––––­­­––––––––– = ––––––– : ––––––– .

· ·

2. Пусть на плоскости (; ¯ даны: проективная система координат R = {A₁, A₂, A₃, E}, прямая a; ¯ и на ней 4 точки A(a₁, a₂, a₃), B(b₁, b₂, b₃), C(c₁, c₂, c₃), D(d₁, d₂, d₃). Требуется найти (ABCD). Для этого нам потребуется следующая теорема.

Теорема 4.2.2. Сложное отношение сохраняется при центральном проецировании.

Пусть точки A, B, C, D прямой a; ¯ проецируются из центра S в точки A, B , C , D прямой a(;¯ . Пусть R = {A₁, A₂, E} – произвольный репер

н а a; ¯, а A₁, A₂ , E – проекции точек A₁, A₂, E из S на a(;¯ . Тогда R = {A₁, A₂ , E} – репер на a(;¯ . Тогда согласно п^о 2.1 точки A, B , C , D имеют в репере R  такие же координаты, что и точки A, B, C, D в репере R . Из теоремы 4.2.1 вытекает, что (ABCD) = (AB C D).

Спроецируем A, B, C, D из центра A₃ на прямую A₁A₂. Проекции этих точек в репере R ₃ = {A₁, A₂, E₃} (E₃ – проекция точки E) будут иметь

координаты A; ̃(a₁, a₂), B; ̃(b₁, b₂) C; ̃(c₁, c₂), D; ̃(d₁, d₂). Значит,

(ABCD) = (A; ̃B; ̃C; ̃D; ̃) = –––––– : –––––­– .

Вместо a₁, a₂ можно брать a₂, a₃ или a₁, a₃ ; это касается и координат других точек.

Теорема 4.2.3. Сложное отношение сохраняется при любом проективном преобразовании плоскости.

Пусть f – проективное преобразование плоскости (; ¯, которое задается реперами R и R  . Пусть точки A, B, C, D на прямой a; ¯ имеют координаты в репере R : A(a_i ), B(b_i ), C(c_i ), D(d_i ), и пусть при преобразовании f они переходят в A, B , C , D. Тогда в репере R  : A(a_i ), B (b_i ), C (c_i ), D(d_i ). Значит, (ABCD) = (AB C D) .

3. Пусть в плоскости (; ¯ даны 4 точки A(a₁, a₂, a₃), B(b₁, b₂, b₃), C(c₁, c₂, c₃), D(d₁, d₂, d₃), лежащие на одной прямой. Тогда

c_i = ₁a_i + ₁b_i , d_i = ₂a_i + ₂b_i , i = 1, 2, 3,

и из формулы (4.2.1) вытекает

(ABCD) = : (4.2.4)

4. Теорема 4.2.4. Если A, B, C, D a; ¯ и точка D в репере R = {A, B, C} имеет координаты u₁ , u₂ , то (ABCD) = u₁/u₂ .

A(1, 0), B(0,1), C(1, 1), D(u₁, u₂)  ₁= ₁ =1, ₂= u₁, ₂= u₂ 

 (ABCD) = u₁/u₂ .

Следствия. 1.  A, B, C a; ¯ R  D a; ¯ : (ABCD) =  .

2. Проективные координаты не зависят от выбора точки O (см. п^о 2.1).