2.6. Формулы замены проективных координат на плоскости.

Рассмотрим на плоскости (; ¯ два проективных репера R = {A₁, A₂, A₃, E} и R = {A₁ , A₂ , A₃ , E}. Пусть M(; ¯ – произвольная точка, и M(x₁, x₂, x₃)_R , M(x₁, x₂ , x₃ )_{R } . Будем писать коротко: M(x_i )_R , M(x_i )_{R } . Согласно определению 2.3.4., x_i – это координаты некоторого вектора x;\s\up8(( на прямой OM в некотором базисе B = {a1;\s\up8(( , a2;\s\up8(( , a3;\s\up8(( }, а x_i – это координаты некоторого вектора x(;\s\up8(( на той же прямой OM в другом базисе B  ={a1(;\s\up8(( , a2(;\s\up8(( , a3(;\s\up8(( }. Поскольку векторы x;\s\up8(( и x(;\s\up8(( должны быть коллинеарны, то x(;\s\up8(( = x;\s\up8(( и x(;\s\up8(( (x_i)_B .

Разложим векторы базиса B  по базису B : ai(;\s\up8(–( =(;\s\do10(k=1c_kiak;\s\up8(–( . Тогда матрица C = [c_ik], i, k = 1, 2, 3 называется матрицей перехода от базиса B к базису B  . Как известно, det C  0 и координаты x_i и x_i вектора x(;\s\up8(( в различных базисах связаны формулами:

x_i = (;\s\do10(k =1c_ik x_{k . (2.6.1)}

эти же формулы показывают связь проективных координат x_i и x_i одной и той же точки в разных реперах на плоскости. В частности, поскольку в репере R  A₁ (1, 0, 0), A₂ (0,1, 0), A₃ (0, 0, 1), E(1, 1, 1), то в репере R :

A₁ (c₁₁, c₂₁, c₃₁), A₂ (c₁₂, c₂₂, c₃₂), A₃ (c₁₃, c₂₃, c₃₃),

E(c₁₁₊c₁₂₊c₁₃, c₂₁₊c₂₂₊c₂₃, c₃₁₊c₃₂₊c₃₃).

Замечание 1. Формулы (2.6.1) имеют место и для преобразования координат точек на прямой, при условии, что индексы i, k принимают значения 1, 2.

Замечание 2. Если обозначить X и X – столбцы составленные из координат векторов x;\s\up8(–( и x(;\s\up8(–( , то формулы (2.6.1) можно переписать в виде одного матричного равенства: X = CX (2.6.1).

2.7. Уравнение прямой на плоскости.

Пусть на проективной плоскости даны две точки A и B, имеющие в проективном репере R координаты A(a₁, a₂, a₃), B(b₁, b₂, b₃). Требуется составить уравнение прямой AB.

П усть M – произвольная точка прямой AB . Ее координаты совпадают с координатами вектора x;\s\up8(( на прямой OM. Координаты точек A и B также совпадают с координатами некоторых векторов a;\s\up8(–( и b;\s\up9(–( на прямых OA и OB. Значит, векторы x;\s\up8((, a;\s\up8(( и

b;\s\up9(( компланарны. И обратно, если x;\s\up8(( компланарен a;\s\up8(( и b;\s\up9((, то M l . Поэтому M AB 

x₁ x₂ x₃

a₁ a₂ a₃ = 0, (2.7.1)

b₁ b₂ b₃

Это и есть уравнение прямой AB.

После раскрытия определителя получим уравнение вида

u₁x₁ + u₂x₂ + u₃x₃ = 0. (2.7.2)

Числа u₁, u₂, u₃ называются координатами прямой. Кроме того, условие коллинеарности векторов x;\s\up8((, a;\s\up8((, b;\s\up9(( можно записать так: x;\s\up8(( = a;\s\up8(( + b;\s\up9((

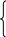x₁ = a₁ + b₁,

x₂ = a₂ + b₂, (2.7.3)

x₃ = a₃ + b₃,

где ,  R – произвольные параметры (² + ²  0). Эти уравнения называются параметрическими уравнениями прямой.

Следствие. Три точки A(a₁, a₂, a₃), B(b₁, b₂, b₃), C(c₁, c₂, c₃) лежат на одной прямой тогда и только тогда, когда существуют ,  R такие, что

c₁ = a₁ + b₁,

c₂ = a₂ + b₂, (2.7.3)

c₃ = a₃ + b₃.