4.3. Гармоническая четверка точек.
Опр. 4.3.1. Упорядоченная четверка точек A, B, C, D прямой называется гармонической, если (ABCD) = –1. При этом точка D называется четвертой гармонической к точкам A, B, C.
Свойства. 1. A, B, C a; ¯ D a; ¯ : (ABCD) = –1.
2. (ABCD) = –1 (CDAB) = –1, (ABDC) = –1, (BACD) = –1.
3. Если C – середина отрезка AB, то четвертой гармоничной к ABC будет несобственная точка.
4. Для A, B, D четвертой гармонической является середина отрезка AB.
Доказательства опираются на определение 4.3.1 и свойства из по 4.1.
О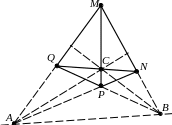
пр.
4.3.2.
Полным
четырехвершинником
называется фигура, которая состоит из
четырех точек расширенной плоскости,
никакие три из которых не лежат на одной
прямой, и шести прямых, которые про-ходят
через все пары этих точек. Точки
называются вершинами,
а прямые – сторонами
четырехвершинника.
Стороны, которые не имеют общих вершин называются противоположными.
Точки A, B, C пересечения противоположных сторон называются диагональными точками, а прямые, которые проходят через пары этих точек называются диагоналями (AB, AC, BC).
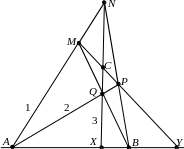
Теорема 4.3.1. На каждой диагонали есть гармоническая четверка точек, состоящая из двух диагональных точек и двух точек пересечения этой диагонали со сторонами, которые проходят через третью диагональную точку.
Докажем, например,
что A,
B,
X,
Y
– гармоническая четверка (см. чертеж).
Для этого спроецируем эти точки из
точки N
на прямую MP;
получим M,
P,
C,
Y.
Затем спроецируем полученные точки
из Q
на прямую AB;получим
B,
A,
X,
Y.
Поскольку сложное отношение сохраняется при центральном проецировании, то
(ABXY ) = (BAXY ) = (ABXY )2 = 1 (ABXY ) = 1.
Н о (ABXY ) = 1 X = Y . Значит, (ABXY ) = –1 .
Эта теорема позволяет строить четвертую гармоническую точку.
Пусть даны точки A, B, X ; требуется построить четвертую гармоническую к ним точку Y . Строим
1. две произвольные прямые 1, 2, проходящие через A ;
2. произвольную прямую 3, проходящую через X ;
3. пересечение прямой 3 с прямыми 1, 2 – точки N, Q ;
4. прямые BQ и BN ;
5. точки M, P, прямую MP ;
6. MP AB = Y .
Вопросы и упражнения.
1. Зачем вводится понятие «сложное отношение 4 точек», как оно
определяется?
2. Доказать свойства 3 – 6 сложного отношения (по 4.1).
3. (ABCD) = 3. Найти сложное отношение четверок, которые получаются из
A, B, C, D различными перестановками.
4. A, B, C, D лежат на одной прямой, при этом AB = BC = CD . Найти
(ABCD) , (ACBD) , (BCDA)
5*. От чего зависит знак (ABCD) ?
6. Когда (ABCD) = 1, (ABCD) = 0?
7. С – середина отрезка AB, D – несобственная точка прямой AB. Найти (ABCD), (ACBD) , (ADBC), и т. д.
8. На плоскости (; ¯ даны точки A(1, 2, –1), B(3, 3, 2), C(2, 1, 3), D(4, 5, 1); убедитесь, что эти точки лежат на одной прямой. Найдите (ABCD), (ACBD) , (BCDA) по формуле а) (4, 2, 1); б) (4, 2, 2). Найдите координаты
а) точки D в репере R ={A, B, C}; б) точки A в репере { B, C, D};
в) точки D в репере R ={A, C, B}.
9. Докажите следствия 1, 2 из теоремы 4.2.4.
10. Является ли понятие «сложное отношение» проективным?
11. Даны 3 точки на прямой. Построить четвертую гармоническую к ним
точку с помощью а) теоремы 4.2.4; б) теоремы 4.3.1.
12. Рассмотреть теорему 4.3.1 в случае, когда четырехвершинник – это
а) трапеция; б) параллелограмм (с продолжением сторон и диагоналей).