Глава 13 Геометрические объекты дифференциальной геометрии

13.1 Кривые. Способы задания кривых

Кривую на плоскости можно изобразить уравнением между текущими координатами ее точек.

Если кривая определяется по отношению к декартовой системе координат, то ее уравнение запишется в виде

F( x, y ) = 0

(13.1)

или, предполагая данное уравнение разрешенным относительно ординаты y , в

виде
y = f ( x ).	(13.2)
Если же кривая определяется по отношению к полярной системе
координат, то ее уравнение имеет форму
F(r,ϕ)= 0 ,	(13.3)
или в форме
r = f (ϕ).	(13.4)

Другим, достаточно удобным способом задания, кривой служит, так называемое, параметрическое изображение кривой, при котором каждая из двух ее текущих координат задается как функция некоторого параметра. Например, в

декартовых координатах кривая может быть задана двумя уравнениями:
x = x(t),	y = y(t).	(13.5)
Исключая из двух последних уравнений вспомогательный параметр t ,
получим одно соотношение между x и		y вида (13.1). Наоборот, из уравнения

(13.1) можно получить разнообразными способами параметрическое изображение кривой. Действительно, если в уравнение (13.1) подставить вместо x произвольную функцию какого-либо параметра t , то оно определит y как

функцию1) того же параметра t , и получим уравнения кривой в форме (13.5). Параметр t , входящий в уравнение (13.5), может иметь иногда какое-либо

механическое или геометрическое значение, связанное со способом образования кривой.

Если, например, представить себе кривую как путь (траекторию), описываемый точкой, движущейся по какому-либо закону, то в каждый данный момент t точка будет занимать на плоскости определенное положение. В этом случае естественно координаты x , y движущейся точки считать функциями

времени t .

Параметр t может иметь и геометрическое значение (угол, расстояние и т.д.) в зависимости от данного геометрического происхождения кривой.

1) Эта функция, как известно, не всегда будет однозначной.

312

Все функции F( x, y ) , f ( x ), x( t ), y( t ) , входящие в уравнения кривой той

или другой формы из указанных выше, будем предполагать непрерывными и имеющими производные 1-го, 2-го, а в нужных случаях и высшего порядков по соответствующим аргументам.

Если левая часть уравнения (13.1) является алгебраической функцией координат x и y , то линия, им изображаемая, называется алгебраической

линией. В этом случае левую часть уравнения можно считать приведенной к целому рациональному виду, т.е. F( x, y ) можно считать многочленом

относительно x и y . Степень (наивысшая) многочлена F( x, y ) называется

порядком линии, определяемой уравнением (13.1). Если кривая (13.1) и прямая Ax + By + C = 0 даны в одной и той же системе координат, то система уравнений

F(x, y)= 0,

будет иметь число решений, равное степени первого уравнения.

Ax + By + C = 0

Таким образом, порядок линии определяет максимальное число ее точек пересечения с произвольной прямой. Порядок линии является ее инвариантным свойством, не зависящим от того, к какой именно декартовой системе координат отнесена линия.

Общее уравнение кривой порядка n содержит один свободный член, два члена с первыми степенями x и y , три члена 2-й степени, …, n +1 членов n -й

степени, всего:

1 + 2 + 3 + ... +( n +1) = (n +1)(n + 2)

2

	членов. Поэтому для определения отношений всех коэффициентов к одному из
	них необходимо дать число точек, лежащих на кривой, равное
		(n +1)(n + 2)−1 =			n(n + 3)		.
	2			2
		Итак, кривая n -го				порядка определяется числом		точек, равным
		n(n + 3)	; но,	разумеется,		при некоторых специальных		расположениях
	2

выбираемых точек указанное их число может оказаться недостаточным для определения единственной линии n -го порядка, содержащей все эти точки.

Так как два уравнения

F( x, y ) = 0 , f ( x, y ) = 0 ,

одно из которых степени n , другое степени m , имеют, как известно, nm

решений, то линия порядка n пересекает линию порядка m в nm точках. Если же окажется, что две линии указанных порядков имеют число общих точек, большее чем nm , то это обстоятельство означает, что одна из этих линий или обе распадаются, т.е. левые части их уравнений имеют общий множитель в виде рациональной функции от x и y . Действительно, для определения, например,

абсцисс точек пересечения мы должны исключить y из уравнений данных линий

В результате чего получим уравнение вида

R( x ) = 0

313

степени nm (левая часть этого уравнения будет результантом). Если число точек пересечения данных линий больше nm , то результант должен тождественно обращаться в нуль (при всяком x ). Но если результант тождественно равен нулю, то два уравнения наших линий имеют общие решения относительно y при любом

x ; такие общие решения могут быть выделены способом последовательных делений, т.е. F (x, y) и f (x, y) имеют общий рациональный множитель, и данные

кривые распадаются.

13.2 О касательных и нормалях

1 Касательная
Пусть кривая задана уравнениями в параметрической форме:
x = x(t),	y = y(t).	(13.6)

Уравнение прямой, проходящей через две точки с координатами M1(x1; y1 ) и

M 2 (x2 ; y2 ), имеет вид:

x − x1

=

y − y1

.

(13.7)

x

2

− x

y

2

− y

Здесь x

1

1

и

y

- текущие координаты точек прямой. В дальнейшем мы текущие

координаты

точек

прямой будем

обозначать через

X

и Y , а

координаты

выбранной

точки

кривой через x

и y . Применяя

формулу (13.7), составим

уравнение

секущей, проходящей

через две точки

кривой

M (x; y) и

′

+ ∆y):

M (x + ∆x; y

X − x

=

Y − y

.

(13.8)

∆x

∆y

Умножим обе части полученного равенства на ∆t :

	X − x			=	Y − y		.		(13.9)
	∆x					∆y
	∆t					∆t
И определим касательную в точке M кривой как предельное положение
секущей MM ′, когда точка M ′ неограниченно приближается к точке M . Заметив
при этом, что
	lim	∆x = x′,						lim	∆y = y′,
∆t →0		∆t						∆t →0	∆t
получим уравнение касательной в виде
	X − x			=		Y − y		.	(13.10)
	x′					y′
								если уравнение кривой дано в форме y = f ( x ), то, полагая
В частности,
x = t , найдем x′ =1,							y′ = dydx , и уравнение касательной примет вид:
						′			(13.11)
Y − y = y (X − x).

Если уравнение кривой дано в форме F( x, y ) = 0 , то

314

y′ = −

дF

дF

:

.

дx

дy

Подставляя найденное в (13.10) имеем

(X − x)

дF

+ (Y − y)

дF

= 0 .

(13.12)

дx

дy

Перепишем уравнение (13.11) в виде

X − x

=

Y − y

,

дx

дy

тогда уравнение (13.12) можно получить, написав, что dF = 0 или

дF

dx

+

дF

dy = 0 ,

дх

дy

и вставив вместо dx и dy им пропорциональные выражения X − x и Y − y ; таким

способом опять получаем:

(X − x)ддFx + (Y − y)ддFy = 0 .

Если уравнение кривой дано в полярных координатах r = f (θ), то, пользуясь формулами x = r cos θ, y = r sinθ, получим параметрические уравнения кривой

	x = f (θ)cos θ,				y = f (θ)sin θ,
и тогда уравнение касательной найдется по формуле (13.10).
Если для координат			x ,		y выбранной точки одновременно выполняются
условия				дF
	дF	= 0 ,			= 0 ,
				дy
	дx

то уравнение касательной (13.12) становится неопределенным; точки кривой, удовлетворяющие указанным условиям, называются ее особыми точками.

Допустим далее, что при параметрическом изображении кривой

уравнениями (13.5)	для	некоторого	значения	t0 параметра	t	выполняется
одновременно
x′(t0 )= 0 ,		y′(t0 )= 0 .
Будем предполагать,	что	функции	x(t) и y(t)	однозначны	и	вблизи t = t0

разложимы в ряд по формуле Тейлора. Пусть, для общности рассуждения,
ближайшая, не равная нулю, при t = t0							производная от x(t)			будет порядка p и
ближайшая, не равная нулю, производная от y(t) будет порядка q . В этом случае
x(t)− x	0	=	(t − t0 )p			x(p)(θ ),	t	0	< θ < t ,
				p!	1				1
y(t)− y0		=		(t − t0 )q		x(q)(θ2 ),	t0 < θ2 < t .
				q!

Уравнение секущей через точку (x0 ; y0 ) примет вид

315

X − x0

y(q)(θ

2

)=

Y − y0

(t − t

0

)p −q x(p)(θ ).

(13.13)

q!

p!

1

Если перейти к пределу,

полагая, что t → t0 , то θ1

и θ2 будут стремиться также к

t0 .

При p = q

уравнение (13.13)

в пределе даст уравнение касательной в

виде

X − x0

=

Y − y0

.

y(q)(t0 )

x(p)(t0 )

Если p > q , то уравнение (13.13) при переходе к пределу даст

X − x0 = 0 ,

т.е. уравнение касательной, в данном случае параллельной оси Oy .

Если p < q , то уравнение (13.13) при переходе к пределу даст

Y − y0 = 0 ,

т.е. уравнение касательной, параллельной оси Ox .

Таким образом, при параметрическом изображении кривой уравнениями (13.5), где x(t) и y(t) - функции, однозначные и разложимые вблизи t = t0 по

формуле Тейлора, мы всегда получаем единственную определенную касательную для каждого значения параметра t0 , для которого указанные условия

выполняются.

2 Нормаль

Назовем нормалью к кривой в точке M (x; y) прямую, проходящую через

выбранную точку кривой перпендикулярно к ее касательной в той же точке.

Запишем условие перпендикулярности двух лучей с угловыми коэффициентами k и k1

1 + kk1 = 0

или

k1 = − 1k .

Далее, по угловому коэффициенту касательной составим угловой коэффициент нормали, а затем и само уравнение нормали.

Если кривая определяется уравнениями одной из указанных выше форм (13.1), (13.2), (13.5), то угловой коэффициент касательной будет иметь одно из следующих выражений:

			дF				дF			y′
k	= −		дx		,	или k =		,	или k =		,
			дF				дx			x′
а потому			дy

316

дF

k

= −

дy

,

или

k = −

1

,

или

k

= −

x′

.

1

дF

1

дF

1

y′

дx

дx

Уравнение нормали в каждом из этих случаев составится, как уравнение

прямой, проходящей через точку

(x; y)

и имеющей угловой коэффициент k1 ,

именно в виде
Y − y = k1(X − x).
Все сказанное выше обобщим таблицей № 1.
Таблица № 1
Уравнение кривой	Уравнение касательной
F( x, y ) = 0	(X − x)		дF	+ (Y − y)			дF		= 0
								дy
			дx
y = f ( x )	Y − y =				дy	(X − x)
					дx
x = x(t),		X − x			=	Y − y
			x′			y′
y = y(t)

Уравнение нормали

		X − x				=	Y − y
			дF						дF
			дx						дy
	Y − y = −					1			(X − x)
						дy

дx

(X − x)x′ + (Y − y)y′ = 0

13.3 Кривизна линий. Радиус и центр кривизны. Натуральное уравнение кривой

Всякую линию, отличную от прямой, мы называем кривой. Сравнивая кривую с ее касательной в какой-либо ее точке, будем говорить, что кривая в этой точке имеет большую или меньшую кривизну, если она вблизи рассматриваемой точки быстрее или медленнее удаляется от прямой – своей касательной. Постараемся дать точное математическое определение кривизны кривой и выбрать какое-либо определенное число, как характеристику, как меру кривизны кривой в рассматриваемой ее точке.

Простейшей кривой, хорошо нам знакомой, является окружность; при этом очевидно, что окружность вполне можно признать за линию с неизменной (одинаковой) кривизной во всех ее точках, т.к. любая дуга окружности, взятая вблизи какой-либо ее точки без изменения, вполне совмещается со всякой другой частью той же окружности (при равных длинах дуг).

Окружность независимо от места, занимаемого ею на плоскости, вполне определяется своим радиусом, поэтому ее радиус мог бы служить и характеристикой ее кривизны, т.е. чем больше радиус, тем меньшую кривизну она имеет и наоборот, чем меньше радиус

Рисунок 106

317

K = lim

∆s→0

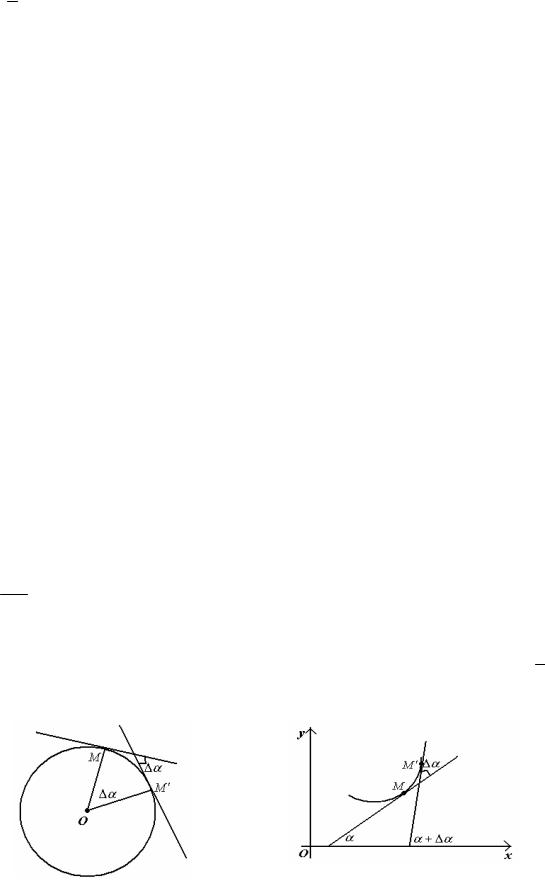
окружности, тем больше ее кривизна. Поэтому совершенно естественно за меру кривизны окружности в каждой ее точке выбрать обратную величину радиуса,

именно 1r .

За направление кривой в каждой ее точке будем считать направление ее касательной в этой точке. Тогда за характеристику кривизны кривой на некотором ее участке можем считать большее или меньшее уклонение касательной в конечной точке участка от касательной в начальной ее точке. Пусть достаточно близкие точки M и M ′ заданной кривой ограничивают дугу MM ′ = ∆s . Назовем угол между касательными в этих точках углом смежности, обозначим его ∆α

(рисунок 106). Тогда выражение

∆α

∆s

может быть названо средней кривизной кривой на протяжении ее дуги ∆s . Очевидно, чем меньше ∆s , тем лучше это отношение будет характеризовать кривизну кривой вблизи начальной точки M ; поэтому кривизной кривой в точке M назовем предел этого отношения, когда точка M ′ неограниченно приближается к точке M , или, что то же самое, когда ∆s стремится к нулю. Итак, за кривизну K кривой в точке M примем выражение:

∆∆αs .

Нетрудно убедиться, что это определение кривизны кривой дает, в частности, для окружности ту же характеристику ее кривизны, какую мы выбрали для нее выше. Действительно, угол (рисунок 107) двух близких касательных равен углу нормалей кривой в соответствующих точках; но для окружности ее дуга ∆s равна радиусу, умноженному на соответствующий центральный угол (угол двух

нормалей), т.е.

∆s = r∆α .

Поэтому

∆∆αs = 1r .

Таким образом, для окружности средняя кривизна любого ее участка постоянна и равна обратной величине ее радиуса. То же значение 1r будет иметь для окружности предел указанного отношения, когда ∆s → 0

Рисунок 107

318

Рисунок 108

Рассмотрим теперь произвольную кривую и пусть ее касательная в какойлибо точке M образует с осью абсцисс угол α , тогда касательная в точке M ′, близкой к первой, будет наклонена к оси Ox под углом α + ∆α . Угол (α + ∆α)−α = ∆α будет углом поворота от первой касательной до второй, т.е. углом смежности двух близких касательных (рисунок 108. Так как α можно считать функцией длины дуги s (непосредственно или через посредство того параметра, функциями которого определяются координаты точек кривой), следовательно, кривизна в точке M выразится формулой

	K = lim	∆α	или	K = dα .
	∆s→0	∆s		ds
	Так как угол α (а, следовательно, и dα ) измеряется отвлеченным числом,
	а дуга s (и ds )		зависит от выбранной линейной единицы масштаба, то
	подразмерность кривизны кривой K будет равной −1 относительно линейной
	единицы. Таким образом,			размерность ее обратной величины	1	будет равной
					K

единице. Это замечание означает, что число K1 при изменении линейной единицы масштаба будет изменяться так же, как будут изменяться и все другие числа,

измеряющие те или иные отрезки. Вот почему число K1 мы имеем право считать

за число, измеряющее некоторый отрезок. Назовем число K1 радиусом кривизны

кривой в данной точке и обозначим через r : r = K1 ,

или

K = 1r .

Согласно определению, кривизна (так же, как и радиус кривизны) может быть и положительной, и отрицательной в зависимости от знака dα или ∆α при положительном ds и ∆s . Если ∆α положительно, то касательная в точке M ′ от касательной в точке M повернута в положительном направлении. Следовательно, вогнутость кривой находится в сторону положительного направления нормали (т.к. нормаль получается поворотом касательной в положительном направлении

		π		M	′	от касательной
	на угол	2 ). Если же ∆α	отрицательно, то касательная в точке
	в точке	M повернута	в отрицательном направлении, т.е.	вогнутость кривой

обращена в сторону отрицательного направления нормали. Обратно, если r положительно, то dα и ∆α положительны, а потому вогнутость кривой обращена в сторону отрицательного направления нормали.

319

Поскольку радиус кривизны является отрезком, мы можем условиться откладывать его по нормали от точки кривой. При этом, если r положителен, то мы его будем откладывать от точки кривой по положительному направлению нормали. Конец радиуса кривизны, отложенного по нормали от точки кривой, назовем центром кривизны в данной точке кривой.

Пусть кривая теперь задана параметрическими уравнениями
x = x(t),	y = y(t).

Найдем выражение кривизны в декартовых координатах.

Так как угол касательной с осью абсцисс в этом случае равен

α = arctg xy′′ ,

то

dα = x′y′′ − x′′y′dt ; x′2 + y′2

причем

ds = x′2 + y′2 dt .

Следовательно, кривизна кривой определяется соотношением

	dα		′ ′′	′′ ′
K =		=	x y	− x y	,
	ds		(x′2 + y′2 )32

а радиус кривизны соотношением

r= (x′2 + y′2 )32 .

x′y′′− x′′y′

Если кривая дана уравнением y = f (x) ,

то ее кривизна и радиус кривизны определяется формулами:

	y	′′					′2	32
K =				,	r =	(1 + y		) .
		3	2			y	′′
	(1 + y′2 )

Найденные выражения показывают, что радиус кривизны кривой в какойлибо ее точке есть радиус окружности, соприкасающейся с кривой в данной ее точке. Центр кривизны в данной ее точке будет центром соответствующей этой точке соприкасающейся окружности. Кривизна кривой обращается в нуль, а радиус кривизны – в бесконечность в точках перегиба, т.е. в таких точках, в которых касательная прямая имеет с кривой соприкосновение 2-го порядка, или, иначе, соприкасающаяся окружность обращается в прямую линию.

Первоначальное определение кривизны кривой, очевидно, не зависит ни от какой системы координат, поэтому указанное выше выражение радиуса кривизны через декартовы координаты и их производные сохраняется при переходе к любой другой (прямоугольной же) декартовой системе координат. Таким образом,

320

кривизна кривой или радиус кривизны являются инвариантами по отношению к любому преобразованию координат (декартовой к декартову).

Кривизна кривой и ее радиус кривизны кривой, вообще говоря, меняются от одной точки к другой. Следовательно, радиус кривизны является функцией длины дуги, отсчитываемой от некоторой определенной точки кривой. Очевидно, что если выражение радиуса кривизны дано в зависимости от длины дуги, то можно вполне определить вид кривой, не считаясь с ее положением на плоскости.

По этой причине каждое из уравнений
f (r, s)= 0	или	r = f (s)

называют натуральным уравнением кривой.

По выражению радиуса кривизны в функции дуги s легко определить точки перегиба или точки заострения кривой (точки возврата); в самом в первом случае радиус кривизны становится бесконечным, во втором случае он обращается в нуль.

13.4 Эволюта. Эвольвенты

Эволютой, или разверткой, для данной кривой назовем геометрическое место центров ее кривизны. Поскольку центр кривизны является центром соприкасающейся окружности, то эволюта будет

одновременно		и			местом	центров
соприкасающихся окружностей данной кривой.
	Координаты	центра			кривизны	кривой
можно	получить, если к координатам точки M
кривой прибавить соответственно проекции на
оси координат радиуса кривизны, отложенного от
точки	M по нормали кривой. Пусть α					- угол
касательной в точке M с осью Ox (рисунок 109),
тогда угол нормали с той же осью будет α + π .
						2
Таким образом, координаты центра кривизны выражаются							Рисунок 109
Следующим образом:			π
		α +			η = y + r cosα ,
	ξ = x + r cos		2	,

или
ξ = x − r sinα,				η = y + r cosα .							(13.14)
Принимая во внимание выражения
r =	(x′2 + y′2 )32		,	cosα =		x′	,	sinα =		y′	,
	′ ′′	′′ ′		x′		+ y′		x′		+ y′
	x y	− x y			2		2		2		2

окончательно находим:

321

		x′2 + y′2
ξ = x −						y′,
		′ ′′			′′ ′
		x y		− x y
		x′2 + y′2
							x	′
η = y +
		′	′′		′′ ′
		x y		− x y
или же для кривой, заданной уравнением y = f (x),
	1 + y′2				′
ξ = x −		y′′			y ,
	1 + y′2				′
η = y +					x .
		y′′

(13.15)

(13.16)

Чтобы получить простейшие свойства эволюты, удобнее пользоваться ее уравнениями в виде (13.14); взяв дифференциалы от ξ и η , получаем:

dξ = dx − r cosα dα − sinα dr ,			dη = dy − r sinαdα + cosα dr ;
но из соотношений
dx = cosα ,	dx	= sinα ,	dx	=	1
ds	ds		ds		r
следует, что
dx = r cosα dα ,		dy = r sinα dα ,
потому
dξ = −sinα dr ,		dη = cosα dr .			(13.16)

Составим отношение этих дифференциалов и сумму их квадратов:

	dη	= −ctgα ,	dξ2 + dη2 = dr2 ;	(13.17)
	dξ

первое соотношение показывает, что касательная к эволюте имеет направление нормали к кривой. Так как нормаль к кривой проходит через соответствующую точку эволюты, то, следовательно, касательной к эволюте и является сама нормаль к кривой. Иначе говоря, эволюта кривой есть огибающая ее нормалей.

Второе из соотношений (13.17) показывает, что дифференциал дуги эволюты по абсолютной величине равен абсолютному значению дифференциала радиуса кривизны кривой, т.е.

dσ = dr .

Допустим, что на участке кривой, где ее радиус кривизны возрастает, мы в том же направлении будем считать возрастающей и дугу эволюты, тогда

dσ = dr или σ2 −σ1 = r2 − r1 ,

т.е. приращение дуги эволюты равно приращению радиуса кривизны кривой.

Пусть точкам M1 и M 2 (рисунок 110) соответствуют радиусы кривизны

M1N1 = r1 ,	M 2 N2 = r2 ,
тогда дуга эволюты от точки N1 до точки N2 будет:
N1N2 =σ2	−σ1 = M 2 N2 − M1N1.

322

y = y(s);

Рисунок 110

Данная кривая относительно своей эволюты называется эвольвентой или развертывающей последней. На основании предыдущих предложений, если дана некоторая кривая, то ее эвольвенту, очевидно, можем получить следующим построением: на каждой касательной заданной кривой в обратную ее сторону следует откладывать дугу кривой, отсчитанную от некоторой ее произвольной выбранной точки. Нетрудно доказать и непосредственно, что это построение даст бесчисленное множество эвольвент данной линии, т.е. кривых, ортогональных в каждой своей точке к касательным начальной кривой. В самом деле, пусть кривая

изображается уравнениями x = x(s),

будем откладывать на каждой из ее касательных в обратную сторону отрезки, равные s + c , тогда геометрическое место концов этих касательных будет

= x − (s + c)x′,

= y − (s + c)y′;

(13.18)

ξ

η

дифференцируя эти соотношения, получим

′

′

dη = −(s + c)dy

,

dξ = −(s + c)dx

,

откуда

)

′

′

′ ′

′ ′

x dξ + y dη = −(s + c)(x dx

+ y dy

или

′

′

(13.19)

x dξ + y dη = 0 ,

так как

x′dx′ + y′dy′ = 0

в силу условия

x′2 + y′2 =1.

Соотношение (13.19) как раз и показывает нам, что касательная к кривой (13.18) при любом выборе постоянного с перпендикулярно к соответствующей касательной к данной кривой.

Взаимоотношение между данной кривой и ее эволютой на основании предыдущих свойств легко представить себе следующим наглядным способом: допустим, что на линию наложена гибкая нерастяжимая нить определенной

323

длины, закрепленная в какой-либо точке M 3 кривой (рисунок 111); если

сматывать нить, держа ее все время натянутой по направлению касательной в точке ее схода с кривой, то конец нити, занимая последовательно положения Q1,

Q2 , Q3 , … этой линии, и опишет развертывающую данной кривой.

Рисунок 111

Если дано натуральное уравнение кривой r = r(s),

то легко получить натуральное уравнение ее эволюты. В самом деле, будем соответствующими буквами со значком (′) обозначать элементы эволюты. В таком случае имеем:

		′			π			′
	α		=α + 2			,	ds		= dr ,	(13.20)
	r′ =			ds′		dr	dr
					=		= r ds .			(13.21)
				dα′		dα
	Таким образом, исключая из соотношений
	s′ = r(s) ,								r′ = r drds	(13.22)

параметр s (дугу начальной кривой), получим натуральное уравнение эволюты. Возьмем, например, натуральное уравнение циклоиды

r 2 + s2 =16a2 ;	(α)
дифференцируя его, получим
rdr + sds = 0 ,
следовательно,
r′ = −s ;	(β)
присоединяя сюда уравнение
s′ = r	(γ)
и исключая r и s из уравнений (α), (β), (γ), найдем
r′2 + s′2 =16a2 ,

т.е. эволютой циклоиды является та же циклоида (определенным образом расположенная относительно первой).

324

13.5 Соприкасающаяся плоскость
Пусть τ будет вектор касательной к		кривой	в	точке	M (ρ). Возьмем
плоскость,	проходящую через касательную	и еще		через	близкую точку
′	кривой (рисунок 112). Обозначим через		r	вектор,	определяющий
M (ρ + ∆ρ)

какую-либо точку указанной плоскости. Тогда три вектора r − ρ , τ , ∆ρ

будут компланарны, а потому их смешанное произведение обращается в нуль

(r − ρ)τ ∆ρ = 0 .

Рисунок 112

Когда точка M ′ неограниченно приближается к первой точке M , т.е.

когда ∆s стремится к нулю,			левая часть предыдущего уравнения стремится к
определенному пределу и само уравнение принимает вид
′	′′	= 0 .	(13.23)
(r − ρ)ρ ρ

Предельное положение плоскости, проходящей через касательную прямую и близкую точку кривой, называется соприкасающейся плоскостью кривой в заданной ее точке. Уравнение (13.23) является, таким образом, уравнением соприкасающейся плоскости кривой.

Соприкасающуюся плоскость можно было бы определить, как предельное положение плоскости, проходящей через три близкие точки кривой, когда две из них стремятся к совпадению с третьей.

Для плоской кривой соприкасающаяся плоскость будет одной и той же во всех точках кривой, именно, плоскостью самой кривой.

Если не делать предположения, что ρ есть функция дуги s , то уравнение (13.23) напишется в виде

(r − ρ)	dρ		dsd 2 ρ − dρ d 2 s		= 0
	ds			ds2
или по упрощении
(r − ρ)dρ d 2 ρ = 0 ;					(13.24)

отсюда следует, что уравнение (11.24) соприкасающейся плоскости сохраняет свой вид и в том случае, когда ρ есть функция любого параметра t .

325

В силу свойств тройного произведения векторов уравнения соприкасающейся плоскости в координатном изображении будет иметь вид

X − x	Y − y	Z − z
x′	y′	z′		= 0 .	(13.25)
x′′	y′′	z′′

Например, составим уравнение соприкасающейся плоскости для кривой, заданной уравнениями

x2a2x2

	+	y2	+	z2	−1 = 0,
		b2		c2

+ y2 + z2 − r 2 = 0.

Решение. Приравнивая нулю полный дифференциал левой части каждого из данных уравнений, мы прежде всего найдем:

dx

=

dy

=

dz

y

z

z

x

x

y

b2

с2

с2

a2

a2

b2

y

z

z

x

x

y

или

1

1

m

1

1 m

1

1

m

dx =

−

,

dy =

−

,

dz =

−

,

c2

x

с2

a2

y

b2

z

b2

a2

где m - некоторый множитель пропорциональности. Отсюда далее получим:

2

1

1

mdx

dm

d

x =

−

−

+

,

c2

x2

x

b2

1

1

mdy

dm

d 2 y =

−

−

+

,

2

2

2

c

a

y

y

2

1

1

mdz

dm

d

z =

−

−

z2

+

z

;

b

a2

2

здесь коэффициенты

при dm

пропорциональны dx , dy , dz , поэтому при

подстановке вторых дифференциалов в уравнение (13.25) члены с dm выпадают. Итак, уравнение искомой соприкасающейся плоскости может быть

написано в следующем виде:

X − x	1						−	1			1					1						−	1			2		1
									c2															c2
	b2										x					b2										x3
Y − y	1						−	1			1					1						−	1			2		1		= 0 ;
								a2															a2					y3
	c2										y					c2
Z − z	1						−	1			1					1						−	1			2		1
									b2															b2
	a2										z					a2										z3

развернув определитель левой части и использовав при этом для координат x , y , z точки касания уравнения самой линии, получим

326

r 2 − a2

x3

(X − x)+

r 2 − b2

y3

(Y − y)+

r 2 − c2

z3

(Z − z)= 0 .

b2 − c2 a4

c2 − a2 b4

a2 − b2 c4

Показать, что соприкасающаяся плоскость остается неизменной для всех точек данной кривой, когда последняя распадается (например, при r 2 = b2 ).

13.6 Кривизна кривой

Пусть τ	единичный вектор касательной к кривой	в точке M ,	тогда τ + ∆τ
- вектор касательной в точке M ′, близкой к первой.		Перенесем	параллельно
вектор τ + ∆τ	в точку M (рисунок 113). В этом случае вектор		∆τ =	TP	по

величине и направлению будет давать уклонение касательной при переходе от точки M к точке M ′. Отношение

∆τ ∆s

возьмем за

меру

кривизны кривой на протяжении

дуги MM ′ = ∆s . Предел

указанного отношения (когда ∆s стремится к нулю)

dτ

ds

называется вектором кривизны кривой в точке M .

Пусть P

- конец вектора τ + ∆τ , параллельно перенесенного в точку M , и

µ - угол (PMT )

двух близких касательных. Тогда

∆τ

=

TP

=

TP

TP

=

TP

µ

,

∆s

∆s

∆s

∆s

TP

TP

где TP - дуга окружности радиуса MT =1. Так как

lim

TP

=1,

TP

то предыдущее соотношение при переходе к пределу

даст величину вектора кривизны в виде

Рисунок 113

dτ

=

lim

µ

.

ds

∆s→0 ∆s

Так как µ есть число, a

∆s - длина дуги кривой,

то,

соблюдая размерность

найденного отношения, можем положить

dτ

=

lim

µ

=

1 ,

ds

∆s→0 ∆s

r

предполагая,

что

r

есть некоторая длина. Величина

1

называется кривизной

r

кривой в данной точке, а

r

называется радиусом кривизны кривой в данной

точке.

327

Отношение ∆µs можно называть средней скоростью поворота вектора τ на

единицу пройденной дуги ∆s кривой. Предел этого отношения называется скоростью вращения вектора τ . Доказанное выше предложение обозначает, что в каждой данной точке кривой скорость вращения вектора τ равна кривизне

кривой в данной точке.

Возвращаемся к вектору кривизны

dτ = d 2 ρ ; ds ds2

само построение показывает, что он направлен в сторону вогнутости кривой.

Далее, так как τ 2 =1 и τ ddsτ = 0, то вектор кривизны перпендикулярен к

касательной. Наконец, уравнение соприкасающейся плоскости

(r − ρ)ρ′ρ′′ = 0

удовлетворяет любой точкой r = ρ + uρ′′

вектора кривизны (считая, что он выходит из точки M кривой). Поэтому вектор кривизны лежит в соприкасающейся плоскости. Единичный вектор, перпендикулярный к касательной, лежащий в соприкасающейся плоскости и направленный в сторону вогнутости кривой (по вектору кривизны), будем называть главной нормалью кривой и обозначать буквой ν («ню» греческое).

Так как величину вектора кривизны мы обозначили через 1r , а его направление через ν , то

dτ

=

ν

;

(13.26)

ds

r

1

при этом согласно условию величина

есть величина положительна и равна

r

1

= +

dτ

2

d 2

ρ 2

(13.27)

= +

.

r

ds

2

ds

Это последнее соотношение легко дает радиус кривизны в координатном изображении

1	= +	d 2 x 2		d 2 y 2			d 2 z		2
				+			+		(13.28)
r			2		ds	2		2
		ds					ds

или в более общем случае, когда x , y , z - функции любого параметра
1		= +	(dsd 2 x − dxd 2s)2 +	(dsd 2 y − dyd 2 s)2 + (dsd 2 z − dzd 2s)2	.	(13.29)
	r			ds2

Из формулы (13.29) можно получить и другое выражение для кривизны. В самом деле, умножая обе части этого равенства векторно на τ , получим

328

[τνr ]= τ ddsτ ,

но по свойству векторного произведения в выражении

dτ = d 2 ρ − d 2 sdρ ds ds2 ds2

можно выбросить последнее слагаемое, как вектор, коллинеарный

	[τν]			=	[dρd	2 ρ]	.
		r			ds	2
Отсюда в силу условий τ 2 =1, ν 2 =1, τν = 0 , найдем
1		=		[dρd 2ρ]2
	r				ds3
или в координатной форме
1		=		(dyd 2 z − dzd 2 y)2 + (dzd 2 x − dxd 2 z)2 + (dxd 2 y − dyd 2 x)2
	r						ds2

τ ; поэтому

(14.30)

. (13.31)

Например, вычислим радиус кривизны линии, определяемой уравнениями

x2

+

y2

+

z

2

−1 = 0,

b2

c

a2

2

2

+ y

2

+ z

2

− l

2

= 0.

x

Решение. Для данной системы уравнений дифференциалы координат определяются соотношениями

dx

=

dy

=

dz

;

1

−

1

1

1

−

1

1

1

−

1

1

c2

a2

b2

b2

x

c2

y

a2

z

отсюда

1

1

m

1

1 m

1

1

m

dx =

−

,

dy =

−

,

dz =

−

,

c2

a2

y

b2

z

поэтому

b2

x

c2

a

2

ds2 = m2α12 ,

где для краткости принято

2

1

1

2

1

1

1 2

1

1

1

2

1

.

σ1 =

−

+

−

+

−

c2

a2

y2

b2

z2

b2

x2

c2

a2

Далее,

1 2

1

m2

1

1

dm

d 2 x = −

−

+

−

,

c2

x3

c2

b2

b2

x

1

1 2

m2

1

1

dm

d 2 y = −

−

+

−

,

a2

y3

a2

c2

c

2

y

329

1

1

2 m2

1

1

dm

d 2 z = −

−

+

−

.

b2

z3

b2

a2

a2

z

При подстановке выражений первых и вторых дифференциалов в формулу (13.31) члены с dm выпадают, а в окончательном результате сокращается множитель m , так что

									1				−				1 1										1									−		1							2 1
																a2																							a
				∑			c2															y					c2														2				y3
									1								1 1										1											1							2 1
													−																							−
1																																								b							z3
		=					a2										b2 z										a2														2										;
	r 2																									σ13
это выражение легко привести к виду
1		=		σ12σ3 −σ22														,
	r 2
								σ13
где															3																												3															3
σ2						1						1								1							1											1								1			+				1		−	1			1		,
		=							−																	+								−
											c2									x4																	a2									y4										b2			z4
			b2																								c2																									a2
σ3						1						1			4					1							1											1					4			1			+				1		−	1		4	1			.
		=							−																	+								−
																				x6																	a2									y6										b2				z6
			b2								c2																c2																									a2

13.7 Подвижной триедр

С каждой точкой кривой можно связать три направления, именно, касательную τ , главную нормаль ν и, наконец, направление, перпендикулярное к двум предыдущим (а следовательно, перпендикулярное к соприкасающейся плоскости), которое мы назовем бинормалью кривой. Бинормаль будем обозначать единичным вектором β и направление ее возьмем так, чтобы в данной

точке кривой три попарно ортогональных вектора τ , ν , β образовали левую

тройку (как и координатные оси).

Три указанных направления называют главными направлениями в данной точке линии.

Согласно определению главных направлений кривой в точке M мы будем иметь между ними следующие соотношения: во-первых, каждый из указанных векторов τ , ν , β будет единичным, поэтому скалярный квадрат каждого из них равен единице:

τ 2 =1,

ν 2 =1,

β 2 =1;

(13.32)

в силу их ортогональности скалярные произведения по два должны обращаться в нуль:

νβ = 0 ,

βτ = 0 ,

τν = 0 ,

(13.33)

а каждый из них будет изображаться векторным произведением двух других в

330

круговом порядке:	ν =[βτ ],	β =[τν].
τ =[νβ],					(13.34)
Наконец, тройное их произведение будет равно единице:
τνβ =1.			точке M можно		(13.35)
Через каждые	два главных	направления в			провести
плоскость (рисунок 114). Плоскость, содержащая векторы τ , ν				и ортогональная к
β , называется соприкасающейся		плоскостью.	Плоскость	через	ν и β ,

ортогональная к касательной τ , называется нормальной плоскостью. Плоскость, содержащая τ и β и перпендикулярная к ν , называется спрямляющей плоскостью кривой по причине, которая будет разъяснена позднее.

Рисунок 114

Три главные плоскости – соприкасающаяся, нормальная и спрямляющая – образуют в каждой точке основной триедр (трехгранник) кривой, который и называется подвижным триедром кривой.

13.8 Кручение кривой

Соприкасающаяся плоскость, направление которой определяется вектором β , для пространственной кривой будет изменяться по мере продвижения по кривой. Это изменение, характеризующее уклонение малого элемента кривой MM ′ от соприкасающейся плоскости в точке M , может быть определено

вектором ddsβ , построенным аналогично вектору кривизны, и называется

вектором кручения кривой в данной точке M . Его величина, очевидно, будет

dβ		= lim	µ′	,
ds			∆s
		∆s→0

где µ′ - угол близких бинормалей кривой.

Установим направление вектора кручения. Так как

	β 2 =1,	β	dβ	= 0 ,
			ds

то он, прежде всего, перпендикулярен к бинормали.

331

Далее, возьмем соотношение

τβ = 0

и продифференцируем его по s , тогда

β

dτ

+τ

dβ

= 0

или

τ

dβ

= 0 ,

ds

ds

ds

так как

β

dτ

=

βν

= 0 .

ds

r

Итак, вектор кручения ddsβ перпендикулярен к бинормали и к касательной,

следовательно, он имеет направление по главной нормали (в ту или другую из ее сторон). Поэтому, очевидно

dβ	=	ν		,	(13.36)
ds			t

где t может принимать как положительные, так и отрицательные значения.

Если поворот вектора β к вектору β + ∆β происходит в положительном направлении (от ν к β и далее) на (положительный) угол µ′, то тогда стрелка

вектора

dβ

противоположна стрелке вектора ν и

1

отрицательно. В этом случае

ds

t

µ′

1 .

lim

= −

∆s→0

∆s

t

β к вектору β + ∆β

Если же поворот

вектора

происходит в отрицательном

направлении (от β к ν ), тогда стрелка вектора

dβ

совпадает со стрелкой вектора

1

ds

′

ν и t положительно, но µ

отрицательно, поэтому опять имеем

lim

µ′

= −

1 .

(13.37)

∆s→0

∆s

t

Итак, соотношение (13.37) будет иметь место в любом случае, как бы ни располагалась кривая вблизи точки M . Величина 1t называется кручением

кривой в точке M , а величина t называется радиусом кручения.

Формула (13.37) означает, что скорость вращения бинормали в каждой точке кривой равна ее кручению в этой точке, взятому с обратным знаком.

Для плоской кривой вектор β имеет постоянное направление (и длину, так как он всегда единичный), а потому

	dβ	= 0 ,	1	= 0
	ds		t

и обратно. Следовательно, кручение плоской кривой равно нулю.

Что касается вычисления самого кручения кривой или его радиуса в общем случае, то здесь неудобно пользоваться тем же приемом, какой применяли при вычислении радиуса кривизны. Действительно, если на основании формулы

332

(13.37) написать, что

1	dβ			2
	=			,
t 2
		ds

то из этого соотношения известна лишь абсолютная величина t (но знак неизвестен). По этой причине нужно получить рациональное выражение для кручения. Из формулы (13.26) имеем

ν= rρ′′,

апотому

β=[τν]= r[ρ′ρ′′];

подставив это выражение для β в формулу (13.36), получим

νt = r[ρ′ρ′′]+ drds [ρ′ρ′′];

умножим теперь обе части этого соотношения скалярно на ν = rρ′′, тогда

1t = r 2 ρ′′[ρ′ρ′′′]= −r 2 ρ′ρ′′ρ′′′

или же

1			r	2	′ ′′	′′′
		= −			ρ ρ ρ		.	(13.34)
t					ρ′′2

Если же перейти к координатам, то кручение кривой изобразится формулой

dx

dy

dz

ds

ds

ds

d 2 x

d 2 y

d 2 z

ds2

ds2

ds2

d 3 x

d 3 y

d 3 z

1

= −

ds3

ds3

ds3

.

(13.35)

t

d 2 x

2

d 2 y

2

d

2 z 2

+

+

2

2

2

ds

ds

ds

z являются функциями произвольного

Если ρ или его координаты x , y ,

параметра, то обобщенные формулы для кручения, как нетрудно проверить, примут вид:

1		= −	dρ d 2 ρ d 3ρ	,						(13.36)
t			[dρ d 2 ρ]2		dx	dy	dz
					d 2 x	d 2 y	d 2 z
1		= −			d 3 x	d 3 y	d 3 z		.	(13.37)
t			(dyd 2 z − dzd 2 y)2 +		(dzd 2 x − dxd 2 z)2			+ (dxd 2 y − dyd 2 x)2

Как кривизна, так и кручение кривой первоначально определены

333

независимо от какой-либо координатной системы, поэтому выражения кривизны и кручения через декартовы координаты и их производные должны оставаться неизменными при переходе к любой другой декартовой системе координат (прямоугольной). Таким образом, координатные выражения кривизны и кручения являются инвариантами кривой по отношению к любому преобразованию координат.

13.9 Формулы Френе-Серре

Мы уже имеем выражение производных от двух главных векторов τ и β :

dτ	=	ν		,	dβ	=	ν		;
ds			r		ds			t

составим теперь производную от третьего вектора

ν =[βτ ].

Дифференцируя указанное его выражение и заменяя производные остальных векторов их значениями, получим

dν

dβ

dτ

ν

ν

β

τ

.

=

τ + β

=

τ

+ β

= −

−

ds

t

t

ds

ds

r

r

Итак, окончательно

dτ

=

ν

,

dν

= −

β

−

τ

,

dβ

=

ν

;

(13.37)

ds

t

t

ds

t

r

ds

полученные соотношения, выражающие производные главных векторов, разложенные по направлениям последних, называются формулами Френе-Серре. Формулы Френе-Серре играют весьма существенную роль при исследовании свойств пространственных линий.

13.10 Натуральные уравнения кривой
Когда радиусы кривизны и кручения кривой r и t		даны как функции s , то
соотношения	t = t(s)
r = r(s),		(13.22)

являются натуральными уравнениями пространственной кривой. Этими уравнениями сама пространственная кривая определяется вполне, не считая ее расположения в пространстве.

Радиусами кривизны и кручения r(s) и t(s), заданными в функциях дуги s , определяется единственная кривая, если не считать ее произвольного перемещения (переноса и поворота) в пространстве.

На этом основании уравнения
r = r(s),	t = t(s)

называют натуральными уравнениями кривой. Натуральные уравнения кривой вполне характеризуют (определяют) кривую независимо от какой-либо системы координат.

334

13.11 Вопросы для самоконтроля

1 Запишите общий вид уравнения кривой на плоскости, заданной в декартовой системе координат (в полярной системе координат).

2Параметрическое уравнение кривой (запишите уравнение, объясните смысл параметра).

3Какая линия называется алгебраической?

4Как определяется порядок линии, определяемой алгебраической функцией?

5Каким числом точек определяется кривая n -го порядка?

6В скольких точках пересекаются линии порядков m и n ?

7Запишите уравнение касательной к кривой, заданной уравнениями в параметрической форме.

8	Запишите	уравнение	касательной	к	кривой,	заданной	уравнением
y = f ( x ).
9	Запишите	уравнение	касательной	к	кривой,	заданной	уравнением
F (x, y)= 0 .

10 Какие точки кривой называются особыми точками?

11 Запишите уравнение касательной, параллельной оси Ox .

12 Запишите уравнение касательной, параллельной оси Oy .

13 Сформулируйте определение нормали к кривой в заданной точке. 14 Какой угол называют углом смежности?

15 Запишите формулу кривизны K кривой в заданной точке. 16 Чему равна средняя кривизна для окружности?

17 Сформулируйте определение радиуса кривизны кривой в данной точке. 18 Запишите формулу для вычисления кривизны кривой.

19 Запишите формулу для вычисления радиуса кривизны кривой.

20 Какое уравнение кривой называют натуральным?

21Сформулируйте определение эволюты кривой.

22Как связаны между собой эволюта и нормали кривой?

23Сформулируйте определение эвольвенты.

24Сформулируйте определение соприкасающейся плоскости кривой.

25Дайте определение вектора кривизны кривой в заданной точке.

26Сформулируйте определение биноминали кривой.

27Какие направления называются главными направлениями в данной точке линии?

28Какая величина называется кручением кривой в точке M ?

29Сформулируйте определение нормальной плоскости.

30Сформулируйте определение спрямляющей плоскости.

31Сформулируйте определение подвижного триедра кривой.

32Запишите зависимость межу скоростью вращения биноминали в каждой точке кривой и кручением в этой точке.

33Чему равно кручение плоской кривой?

34Запишите формулы Френе-Серре.

35Запишите натуральные уравнения пространственной кривой.

335