Глава 2 Комплексные числа

2.1 Система комплексных чисел

На протяжении курса элементарной алгебры несколько раз происходит обогащение запаса чисел. Школьник, приступающий к изучению алгебры, приносит из арифметики знакомство с положительными целыми и дробными числами. Алгебра начинается по существу с введения отрицательных чисел, т.е. с оформления первой среди важнейших числовых систем – системы целых чисел, состоящей из всех натуральных, всех им противоположных чисел и нуля, и более широкой системы рациональных чисел, состоящей из всех целых и всех дробных чисел, т.е. из чисел, представимых в виде десятичной бесконечной периодической дроби, как положительных, так и отрицательных.

Дальнейшее расширение запаса чисел происходит тогда, когда в рассмотрение вводятся иррациональные числа (числа, не представимые в виде десятичных бесконечных периодических дробей). Система, состоящая из всех рациональных и иррациональных чисел, называется системой действительных

(или вещественных) чисел.

С помощью положительных действительных чисел можно выразить результат любого измерения, а с помощью произвольных действительных чисел – изменение любой величины. Арифметические операции (сложение, вычитание, умножение и деление на число, отличное от нуля) над действительными числами снова дают действительные числа. Отсюда следует, в частности, что рациональная функция с действительными коэффициентами принимает действительные значения при всех действительных значениях аргумента, для которых она определена.

Операция же извлечения квадратного корня определена не для всех действительных чисел, а лишь для неотрицательных – из отрицательного числа квадратный корень на множестве действительных чисел извлечь нельзя. Поэтому в теории квадратных уравнений приходится рассматривать три случая: если

D = b2 − 4ac > 0 , то уравнение	ax2 +bx + c = 0 имеет два различных
действительных корня, при D = 0	оно имеет лишь один действительный корень

(второй кратности), а при D < 0 уравнение действительных корней не имеет. Таким образом, ряд вопросов, возникших при решении уравнений второй,

а также третьей, четвертой степеней, привел математиков к необходимости расширить множество действительных чисел, присоединив к нему новое число i ,

такое, что i2 = −1. Поскольку действительных чисел с таким свойством не существует, новое число назвали «мнимой единицей» - оно не выражало ни результатов измерения величин, ни изменений этих величин. Но включение числа i потребовало дальнейшего расширения множества чисел – пришлось ввести произведения этого числа на все действительные числа, т.е. числа вида bi , где b R , а также суммы действительных чисел и таких произведений, т.е. числа вида a + bi , где a, b R . Получившиеся при этом числа были названы комплексными,

так как они содержали как действительную часть а, так и чисто мнимую часть bi .

28

Поскольку выражение a + bi напоминает многочлен первой степени от i (с той лишь существенной разницей, что i не является переменной), математики XVI века производили операции над такими выражениями по тем же правилам,

что и над многочленами, причем когда у них появлялось выражение i2 , его заменяли на – 1.

Например, сумму и произведение комплексных чисел определяли

следующим образом:
(a + bi) + (c + di) = (a + c) + (b + d)i ,	(2.1)
(a + bi)(c + di) = ac + adi + bci + bdi2 = (ac −bd) + (ad + bc)i .	(2.2)

Частное двух многочленов первой степени не выражается, вообще говоря, в идее многочлена. Но для комплексных чисел частное снова выражается в виде комплексного же числа. Именно,

a + bi

=

(a + bi)(c − di)

=

(ac + bd) + (bc − ad)i

=

(ac + bd) + (bc − ad)i

=

c + di (c + di)(c − di)

c2 − d 2i2

c2 + d 2

ac + bd

+

bc − ad

i .

(2.3)

c2 + d 2

c2 + d 2

Из формулы (2.2) вытекает, что

i3 = i2 i = (−1)i = −i ,

i4 = i3 i = (−i)i = −i2 = −(−1) =1,

i5 = i4 i =1 i = i .

Вообще, i4n+k

= (i4 )n ik

=1n ik

= ik .

Например, i67

= i64+3 = i4 16+3 = i3

= −i .

Равенства (2.1), (2.2), (2.3) имеют пока что лишь формальный характер. Далее мы приступим к детальному анализу понятия комплексного числа и

узнаем какие практические приложения имеет теория комплексных чисел.

2.2 Определение комплексных чисел. Операции над комплексными числами алгебраической формы

Неясности, связанные с преждевременным употреблением знаков сложения и умножения, устраняются весьма просто. Ведь в записи a + bi нас интересуют лишь действительные числа a и b, идущие в определенном порядке. Поэтому введем следующее определение.

Комплексным числом z называют пару (a; b) действительных чисел a и b, взятых в определенном порядке. Две пары (a; b) и (c; d) задают одно и то же

комплексное число в том и только в том случае, когда они совпадают, т.е. когда a = c и b = d .

Из этого определения следует, что одно равенство (a; b) = (c; d) для

комплексных чисел равносильно двум равенствам a = c действительных чисел. Если z = (a; b) - комплексное число, то

и b = d для a называют его

действительной частью, b - мнимой частью. Приняты обозначения a = Re z ,

29

b = Im z (от французских слов reele – действительный и imaginaire - мнимый).

Числа вида (0; b) , b ≠ 0 , называют чисто мнимыми числами.

Определим теперь операции сложения и умножения комплексных чисел

(т.е. пар (a; b) ). Пусть z = (a; b) и w = (c; d) , тогда
z + w = (a; b) + (c; d) = (a + c; b + d)	(2.4)
и
zw = (a; b)(c; d) = (ac − bd; ad + bc) .	(2.5)

Итак, мы ввели понятие комплексного числа и определили для этих чисел операции сложения и умножения. Теперь можно перейти к записи комплексных чисел в виде z = a + bi , о которой говорилось выше. Для этого заметим следующее:

для пар вида (a; 0) определенные выше операции сложения и умножения

сводятся к соответствующим операциям над действительными числами, т.е. имеют место равенства:

(a; 0) + (c; 0) = (a + c; 0)	(2.6)
(a; 0)(c; 0) = (ac; 0) ;	(2.7)
(b; 0)(0; 1) = (0; b)	(2.8)
(0; 1) (0; 1) = (−1; 0) .	(2.9)

Эти утверждения непосредственно вытекают из формул (2.4) и (2.5).

Из утверждения (2.6) следует, что пару (a; 0) можно кратко обозначить через а. Тогда равенство (2.9) примет вид: (0; 1) (0; 1) = −1. Наконец, обозначим

пару (0; 1) через i . В этих обозначениях равенство	(2.8) принимает вид:
bi = (0; b) . Поскольку (a; b) = (a; 0) + (0; b) , то получаем,	что пару (a; b) можно
обозначить a + bi :
(a; b) = a + bi .

Теперь уже операции сложения и умножения в правой части равенства имеют смысл.

В дальнейшем мы будем записывать комплексные числа в виде z = a + bi , z = x + iy , z =u + iv и называть эту форму записи алгебраической. Формулы

сложения и умножения комплексных чисел, заданных алгебраической формой приобретают вид:

(a + bi) + (c + di) = (a + c) + (b + d)i	(2.4)`
и
(a + bi)(c + di) = ac + adi + bci + bdi2 = (ac −bd) + (ad + bc)i .	(2.5)`
Свойства операций сложения и умножения для комплексных чисел такие

же, как и для действительных:			zw = wz ,
1)	z + w = w + z ,	4)
2) (z + w) + t = z + (w + t) ,		5) (zw)t = z(wt) ,
3)	z + 0 = z ,	6)	z 1 = z ,
7)	z(w + t) = zw + zt .

30

Кроме того, каждое комплексное число z = a + bi имеет противоположное ему число − z = −a − bi . В самом деле,

(a + bi) + (−a − bi) = (a − a) + (b − b)i = 0 .

Наконец, каждое отличное от нуля комплексное число z имеет обратное ему число, т.е. такое число w, что zw =1. Действительно, будем искать число w в виде w = x + yi. Равенство zw =1 принимает при этом вид (a + bi)(x + yi) =1, т.е.

(ax − by) + (bx + ay)i =1 + i 0 .

(2.10)

Так как комплексные числа равны в том и только том случае, когда у них одинаковы действительные части и мнимые части соответственно, из равенства (2.10) получаем два уравнения для отыскания x и y :

ax − by =1,

bx + ay = 0.

	Решая эту систему уравнений, получаем, что x =		a	, y =	− b	(при
		a2	+ b2		a2 + b2

этом a2 + b2 ≠ 0 , (т.е. z предполагается отличным от нуля). Таким образом, число обратное комплексному числу z = a + bi имеет вид

	w =	1 =	a	−		b	i .	(2.11)
			a2 + b2		a2	+ b2
		z

Итак, все 9 основных свойств операций сложения и умножения действительных чисел, на которых основана алгебра, верны и для комплексных чисел. Отсюда следует, что любое алгебраическое тождество остается справедливым и в комплексной области. Например, для комплексных чисел z и w верны тождества

(z ± w)2 = z2 ± 2zw + w2 ,

(z + w)(z − w) = z2 − w2 и т.д.

Операции вычитания и деления комплексных чисел определяются равенствами

z − w = z + (−w)

и

z

= z

1

, w ≠ 0 .

w

w

Из этих равенств, повторимся, вытекает, что

(a + bi) − (c + di) = (a − c) + (b − d )i

и

a + bi

1

с

d

ac

ad

= (a + bi)

= (a + bi)

−

i

=

−

i +

c + di

c

+ di

+ d 2

с

+ d 2

с2 + d 2

с2

+ d 2

с2

2

+

bс

i +

bd

=

aс + bd

+

bс − ad

i .

с2 + d 2

с2 + d 2

с2 + d 2

с2 + d 2

31

На практике вместо полученной формулы используют уже указанный

прием: умножают числитель и знаменатель дроби

a + bi

на число, сопряженное

c + di

знаменателю, т.е. на c − di и приводят далее необходимые операции:

a + bi

=

(a + bi)(c − di)

=

(ac + bd) + (bc − ad)i

=

(ac + bd) + (bc − ad)i

=

c + di (c + di)(c − di)

c2 − d 2i2

c2 + d 2

=

ac + bd

+

bc − ad

i .

(2.12)

c2 + d 2

c2 + d 2

Комплексное число c − di называется сопряженным комплексному числу c + di , т.е. сопряженные комплексные числа отличаются только знаком мнимой части.

Если z - комплексное число, то сопряженное ему число обозначают z . Рассмотрим произведение сопряженных чисел

z z = (c + di)(c − di) = c2 − (di)2 = c2 + d 2 .

Таким образом, заключаем, что произведение сопряженных комплексных чисел является числом действительным.

НапримерU ,U пусть даны комплексные числа 10 + 8i , 1 + i . Найдем их сумму, разность, произведение и частное.

Решение. а) (10 + 8i)+ (1 + i) = (10 +1) + (8 +1)i =11 + 9i ; б) (10 + 8i) − (1 + i) = (10 −1) + (8 −1)i = 9 + 7i ;

в) (10 + 8i)(1 + i) =10 +10i + 8i + 8i2 = 2 +18i ;

г)

10 + 8i

=

(10 + 8i)(1 − i)

=

10 −10i + 8i − 8i2

=

18 − 2i

= 9 − i .

1

+ i

(1

+ i)(1

− i)

1 − i2

2

Далее, пусть, напримерU

,U требуется найти число,

обратное числу z = 4 + 3i

( a = 4, b = 3).

Решение. Пользуемся формулой (2.10):

z−1 =

4

−

3i

=

4

−

3i

.

42

+ 32

42 + 32

25

25

Комплексное число

4

−

3

i

является обратным числу 4 + 3i и наоборот.

25

25

Поскольку при решении ряда задач на комплексные числа часто используются операции сопряжения, полезно более подробно изучить сопряжение числа.

Итак, числа a + bi и a − bi - сопряженные. Числом, сопряженным действительному числу a , будет само число a ; сопряженное чисто мнимому числу bi - число − bi . Обозначение:

a = a , a R , bi = −bi , b R

32

Верны следующие утверждения:

1) Число, сопряженное сумме комплексных чисел равно сумме чисел, сопряженных со слагаемыми:

z + w = z + w.

Действительно. Пусть z = a + bi , w = c + di , и потому

z+ w = (a + bi) + (c + di) = (a + c) + (b + d )i = (a + c)− (b + d )i =

=(a − bi) + (c − di) = z + w.

2) Число, сопряженное произведению комплексных чисел, равно произведению чисел, сопряженных множителям

zw = z w .

Действительно, если z = a + bi , w = c + di , то

=

=

= (ac − bd )− (ad + bc)i .

z w

(a + bi)(c + di)

(ac − bd) + (ad + bc)i

C другой стороны,

= (a − bi)(c − di)= (ac − bd )− (ad + bc)i .

z

w

Получили одинаковые результаты, что и доказывает верность второго

утверждения.

обратному z ,

3)

Если z ≠ 0 , то число сопряженное числу,

обратно

числу, сопряженному с z :

1

, (т.е.

=1:

).

1

=

1: z

z

z

z

1

Действительно. Из равенства z

=1 следует,

что

1

=1.

Но тогда

z

=1

1

z

z

1

=

.

z

z

Возведение в степень комплексного числа

Выпишем еще раз целые степени мнимой единицы:

i3 = i2 i = (−1)i = −i ,

i4 = i3 i = (−i)i = −i2 = −(−1) =1,

i5 = i4 i =1 i = i ,

i6 = i5 i = i2 = −1,

i7 = i6 i = (−1)i = −i ,

i8 = i7 i = −i i = −i2 =1 и т.д.

В общем виде полученный результат можно записать так:

i4n =1;

i4n+1 = i ;

i4n+2 = −1;

i4n+3 = −i (n = 0, 1, 2,...) .

(2.13)

33

1 2 3

При возведении комплексного числа a + bi во вторую и третью степень пользуются формулой для квадрата и куба суммы двух чисел, а при возведении в степень п (п – натуральное число, n ≥ 4 ) – формулой бинома Ньютона:

(a + bi)n = an + an−1bi + n(1n −21) an−2 (bi)2 + n(n −1)(n − 2) an−3 (bi)3 +... +

+

n(n −

1)...(n − (k −1))

a

n−k

(bi)

k

+... + (bi)

n

.

(2.14)

1

2

3 ... k

Для нахождения коэффициентов формулы (2.14) удобно пользоваться

треугольником Паскаля (смотри практическое занятие).

В правой части этого равенства степени мнимой единицы заменяют по

формулам (2.13) и приводят подобные члены.

НапримерU

,U возведем

комплексное число z = 2 − 3i в третью

степень,

используя формулу куба

суммы

(формулу

бинома Ньютона при

n = 3 ):

(a −b)3 = a3 + 3a2b +3ab2 + b3

и то, что i2 = −1, i3 = −i , имеем:

(2 − 3i)3 = 23 + 3 22 (−3i) + 3 2 (−3i)2 + (−3i)3 =8 − 36i − 54 + 27i =

= −46 −9i .

Таким образом, (2 − 3i)3

= −46 − 9i .

Извлечение квадратного корня из комплексного числа

Квадратным корнем из комплексного числа называется такое комплексное число, квадрат которого равен данному.

Обозначим квадратный корень из комплексного числа x + yi через u + vi , тогда по определению x + yi = u + vi .

Возведем обе части полученного равенства в квадрат

(u + vi)2 = x + yi ,

u2 + 2uvi + (vi)2 = x + yi , u2 + 2uvi − v2 = x + yi ,

(u2 − v2 ) + (2uv)i = x + yi ,

поскольку два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части соответственно, имеем:

u2	− v2 = x ,		2uv = y .	(2.15)
Возведем каждое из этих равенств в квадрат и сложим полученное:
+	(u2 − v2 )2 = x2
	(2uv)2 = y2
(u2 − v2 )2 + 4u2v2 = x2 + y2 ,
u4	− 2u2v2	+ v4	+ 4u2v2 = x2 + y2 ,
u4	+ 2u2v2	+ v4	= x2 + y2 ,
(u2 + v2 )2 = x2 + y2 ,

34

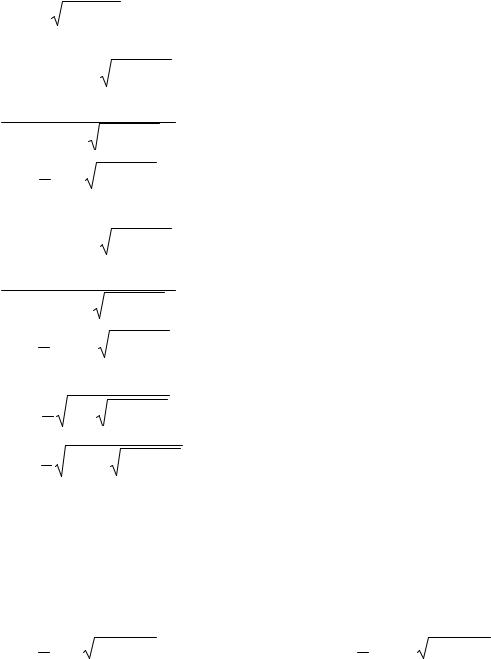
или u2 + v2	=		x2 + y2 .							(2.16)
Почленно сложив равенство (2.16) и первое из (2.15) находим u2 :
	2	+ v		2	=	x	2	+ y	2	,
u
+	2			2
		− v			= x,
u
2u2 = x + x2 + y2 ,
u2 =	1		(x + x2 + y2 ).
	2
Теперь вычтем из (2.16) первое (2.15):
	2	+ v		2	=	x	2	+ y	2	,
u
−	2			2
		− v			= x,
u

2v2 = −x + x2 + y2 ,
v2 =	1 (− x + x2 + y2 ).
	2
Таким образом
u = ± 1		x + x2 + y2 ,
	2
v = ±	1	− x + x2 + y2 .
	2

Знаки u и v выбирают так, чтобы полученные второму из равенств (2.15), то есть равенству 2uv = y .

(2.17)

u и v удовлетворяли

НапримерU		,U извлечем квадратный корень из комплексного числа z = 5 +12i .
Решение.		Обозначим квадратный корень из числа								z через u + vi , тогда
(u + vi)2 = 5 +12i . Поскольку в данном случае x = 5 ,									y =12 , то по формулам (2.17)
получаем:	1 (5 +	52 +122 )=			1			v2 = 1	(−5 +	52 +122 )= 4;
u2 =						(5 +13) = 9 ;
	2			2				2
u2 =	9 ; u = 3 , u		2	= −3; v2 = 4 , v = 2 , v			2	= −2 .
	1			1
Таким образом,				найдено два значения квадратного корня: u1 + v1i = 3 + 2i ,

u2 + v2i = −3 − 2i . (Знаки выбрали согласно второму равенству из (2.15), 2uv = y , т.е. поскольку y =12 > 0 , то u и v одного комплексного числа одинаковых знаков.)

35

2.3 Тригонометрическая форма комплексных чисел. Операции над комплексными числами, заданными в тригонометрической форме

Геометрическое изображение комплексных чисел

Мы дали определение понятию комплексного числа и научились выполнять над комплексными числами арифметические действия, а также извлекать из них квадратные корни. Как уже отмечалось, одним из важнейших, является вопрос о практическом значении комплексных чисел. Чтобы ответить на этот вопрос, нужно сначала научиться изображать комплексные числа геометрически, подобно тому как изображаются действительные числа точками на координатной прямой.

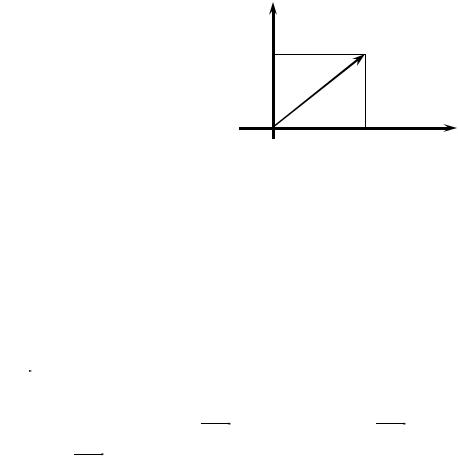
Комплексное число z = x + yi задается парой (x; y) действительных чисел. Рассмотрим эту пару чисел в качестве координат точки M (x; y) на координатной плоскости. Т.е. поставим в соответствие комплексному числу z = x + yi точку плоскости с координатами (x; y) и обозначим ее M (рисунок 13).

y

y

M(x; y)

0

x

x

Рисунок 13

Ясно, что при этом каждая точка координатной плоскости изображает одно и только одно число, а каждое число изображается одной и только одной точкой. Действительным числам соответствуют точки оси абсцисс, а чисто мнимым – точки оси ординат. Поскольку сопряженные числа отличаются только знаком мнимой части, то очевидно, что они изображаются точками координатной плоскости, симметричными относительно оси абсцисс.

Часто вместо точек на плоскости берут их радиус-векторы, т.е. векторы OM , началом которых служит точка O(0; 0) , концом M (x; y) . Ведь для того, чтобы найти координаты вектора надо от координат конца вычесть координаты начала. В нашем случае OM (x − 0; y − 0) , т.е. OM (x; y) , таким образом точка M

и вектор OM имеют одни и те же координаты.

Изображение комплексных чисел с помощью векторов удобно тем, что при этом получают простое геометрическое истолкование операций над ними. Мы знаем, что при сложении комплексных чисел отдельно складываются их действительные и мнимые части:

(a + bi) + (c + di) = (a + c) + (b + d)i .

36

Точно так же, при сложении векторов отдельно складываются их координаты: если OM (a; b) и ON(c; d) , то OM + ON = (a + b;c + d) . Это

означает, что при указанном соответствии операциям сложения и вычитания комплексных чисел соответствуют те же операции над векторами. Иными

словами, если числу z соответствует вектор OM , а числу w - вектор ON , то

числу z + w соответствует вектор OM + ON , а числу z − w - вектор OM −ON . Аналогично, при умножении комплексного числа z на действительное

число а соответствующий ему вектор OM умножается на это же число. Иными словами, числу az соответствует вектор a OM . В самом деле, на а умножаются как обе координаты вектора OM , так и действительная и мнимая часть числа z .

Полярная система координат и тригонометрическая форма комплексных чисел

Положение точки на плоскости можно задать различными способами. До этого момента мы работали с вами только с декартовой системой координат. Познакомимся с полярной системой.

Полярная система координат состоит из точки – полюса и полярной оси. При этом любая точка плоскости задается двумя координатами (r; ϕ),

называемыми полярными координатами: r - длина радиус-вектора точки.

ϕ - величина угла, образованного полярным лучом и радиус-вектором

точки.

Оговоримся заранее, что еще необходимо задать масштаб, ведь длину радиус-вектора надо измерить. Подробнее об этом вы узнаете в теме «Вектора».

В дальнейшем r будем называть модулем, а ϕ - аргументом.

Рисунок 14

Для того чтобы комплексное число z = x + yi записать в

тригонометрической форме совместим декартову и полярную системы координат следующим образом: начало координат совмещаем с полюсом, а ось абсцисс с полярной осью, тогда одна и та же точка М, изображающая комплексное число в

декартовой системе координат будет иметь координаты (x; y) , а в полярной

(r; ϕ).

37

						Рисунок 15
Достроив			чертеж			до прямоугольного			треугольника OBM (гипотенуза
OM = r , катеты BM = y ,						OB = x ) выразим x , y через r , ϕ .
x = r cosϕ,									(2.18)
y = r sinϕ.
Таким образом, комплексное число z = x + yi запишем через r и ϕ :
z = r cosϕ + ir sinϕ						,
z = r(cosϕ + isinϕ).
Из треугольника OBM выразим теперь r и ϕ через x и y .
Имеем r 2 = x2 + y2 (теорема Пифагора)
r = x2 + y2 ,
(знак у корня +, так как r - длина, то есть величина неотрицательная).
Далее, tgϕ =				y	(по определению тангенса острого угла прямоугольного
				x			y
треугольника), следовательно ϕ = arctg								.
							x		z = x + yi однозначным образом
Итак, всякое комплексное число
записывается в виде
z = r(cosϕ + i sinϕ),									(2.19)
где r = x2 + y2		= z ,
ϕ = arctg		y	= arg z .
		x
Причем аргумент ϕ определен лишь с точностью до слагаемых, кратных

2π . Назовем главным аргументом – наименьший положительный.
	Запись комплексного числа (2.19) называется тригонометрической
формой.								π		π
	НапримерU	,U		комплексные	числа	z			+ isin
							= 2 cos	2		2	,
	= cos13π + isin		13			1
z2				π заданы в тригонометрической форме, однако комплексные
	18		18

38

					π				π						2				2				z5 = cos			3	π + i sin			7
числа z3 = (−2) cos						+ isin				,		z4 = 3 cos				π − isin				π ,												π
					5				5						3				3							4				4
даны не в тригонометрической форме, хотя их записи напоминают запись (2.19).
В тригонометрической форме эти числа запишутся так:																								7				7
z			6		+ isin		6			, z			4	π + isin			4				z		= cos		π + isin				π .
	3	= 2 cos		π				π			4	= 3 cos						π ,				5
			5				5						3				3							4				4

Отметим Uособенности тригонометрической формы комплексного числа:U

1)первый множитель – неотрицательное число, r ≥ 0 ;

2)косинус и синус обязательно одного и того же аргумента;

3)мнимая единица умножена на синус угла.

Два комплексных числа, заданных в тригонометрической форме равны тогда и только тогда, когда их модули равны, а аргументы отличаются на величину, кратную 2π . Следовательно, если

r1 (cosϕ1 + isinϕ1 )= r2 (cosϕ2 + isinϕ2 ) , то r1 = r2 , ϕ2 =ϕ1 + 2πk ( k = 0, ±1, ± 2, ...).

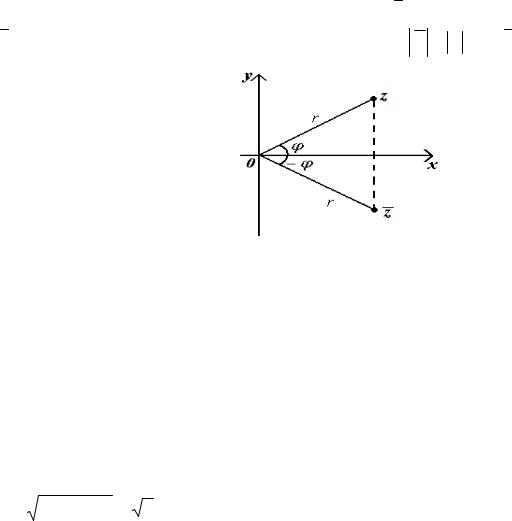
Если комплексное число z = x + yi задано в тригонометрической форме z = r(cosϕ + isinϕ), то сопряженное ему число z = x − yi записывается в форме z = r(cos(−ϕ) + isin(−ϕ)) (см. рисунок 16); поэтому z = z , arg z = −arg z .

		Рисунок 16
	НапримерU	,U запишем комплексное число z =	5 + i	в алгебраической и
			2 + 3i

тригонометрической формах.

Решение. Сначала запишем заданное число в алгебраической форме:

5 + i

=

(5 + i)(2 − 3i)

=

10 −15i + 2i − 3i2

=

10 −15i + 2i + 3

=

13 −13i

=1

− i .

2 + 3i

(2

+ 3i)(2 − 3i)

4

− 9i2

4

+ 9

13

Чтобы записать комплексное число 1 − i в тригонометрической форме, воспользуемся формулами (2.19). Поскольку в данном случае x =1, y = −1, то

r =

2

2

tgϕ =

y

−1

ϕ = −

π

+ 2πk , k Z . Таким

1

+ (−1)

=

2 ,

=

1

, следовательно

4

x

образом, arg z = −

π

+ 2πk , k Z , а главный аргумент −

π

+ 2π =

7π

.

4

4

4

39

Следовательно, комплексное				число			1 − i	имеет следующую
тригонометрическую форму: 1 − i =				7π	+ isin		7π
			2 cos	4			.
							4
Действия	над	комплексными				числами,		заданными	в
тригонометрической форме
Рассмотрим два комплексных числа z1 и z2 , заданных в
тригонометрической форме
z1 = r(cos ϕ + i sin ϕ),		z2 = ρ(cosψ + isinψ ) .						(2.20)
Произведение комплексных чисел
Выполняя умножение чисел (2.20), получаем
z1 z2 = r(cosϕ + isinϕ)ρ(cosψ + isinψ )=
= rρ(cosϕcosψ + i cosϕsinψ + isinϕcosψ − sinϕsinψ )=
= rρ((cosϕcosψ − sinϕsinψ )+ i(cosϕsinψ + sinϕcosψ )),
z1 z2 = rρ(cos(ϕ +ψ )+ i sin(ϕ +ψ )).								(2.21)
Из равенства (2.21) следует, что

z1 z2 = z1 z2 , arg(z1 z2 ) = arg(z1) + arg(z2 ) ,

т.е. модуль произведения комплексных чисел равен произведению модулей сомножителей, а аргументом произведения этих чисел является сумма аргументов сомножителей.

Сумму и разность комплексных чисел, заданных в тригонометрической форме, нельзя выразить формулами, подобными формуле умножения. Однако,

для модуля суммы имеют место следующие важные неравенства:
z1 − z2 ≤ z1 + z2 ≤ z1 + z2 ,	(2.22)

т.е. модуль суммы двух комплексных чисел меньше или равен сумме модулей слагаемых, но больше или равен разности этих модулей.

Неравенства (2.22) можно получить следующим путем. Пусть z1 = r1(cosϕ1 + isinϕ1) , z2 = r2 (cosϕ2 + isinϕ2 ) и пусть тригонометрическая форма

числа z1 + z2 есть z1 + z2 = R(cosψ + isinψ ) . Складывая отдельно действительные

и отдельно мнимые части, получаем: r1 cosϕ1 + r2 cosϕ2 = R cosψ , r1 sinϕ1 + r2 sinϕ2 = Rsinψ ;

умножая обе части первого равенства на cosψ , обе части второго – на sinψ и складывая полученное, имеем:

r1(cosϕ1 cosψ + sinϕ1 sinψ )+ r2 (cosϕ2 cosψ + sinϕ2 sinψ )= R(cos2ψ + sin2ψ ),

т.е.

r1 cos(ϕ1 −ψ )+ r2 cos(ϕ2 −ψ )= R .

40

Отсюда, так как косинус никогда не бывает больше единицы, следует

неравенство

r1 + r2 ≥ R , т.е.

z1

+

z2

≥

z1 + z2

. С другой стороны,

z1 = (z1 + z2 ) − z2 = (z1 + z2 )+ (−z2 ) , но

z1

≤

z1 + z2

+

− z2

=

z1 + z2

+

z2

,

откуда

z1

−

z2

≤

z1 + z2

.

Следует заметить, что для комплексных чисел понятия «больше» и «меньше» не могут быть разумно определены, так как эти числа, в отличие от действительных чисел, располагаются не на прямой линии, точки которой естественным образом упорядочены, а на плоскости. Поэтому сами комплексные числа (а не их модули) никогда нельзя соединять знаком неравенства.

Частное двух комплексных чисел

Пусть заданы комплексные числа (2.20) и пусть z2 ≠ 0 . Рассмотрим

частное

z1

, имеем

z2

= r(cosϕ + isinϕ)(cosψ − isin ρ)

z1

=

r(cosϕ + isinϕ)

=

z2

ρ(cosψ + isinψ )

ρ(cosψ + isinψ )(cosψ − isinψ )

=

r

(cosϕcosψ + sinϕsinψ )+ i(sinϕcosψ + cosϕsinϕ)

,

cos2 ψ + sin2 ψ

ρ

z1

=

r

(cos(ϕ − ψ)+ i sin(ϕ − ψ)).

(2.23)

z2

ρ

Из этой тригонометрической формы частного следует, что

z1

z

1

z1

=

, arg

= arg( z1 ) − arg( z2

) ;

z2

z2

z2

т.е. модуль частного комплексных чисел равен частному модулей числителя и знаменателя, а аргументом частного этих чисел является разность аргументов числителя и знаменателя.

Если

z1 =1 =1(cos 0 + isin 0), z2 = ρ(cosψ + isinψ ) и

ρ ≠ 0 , то формула

(2.23) принимает вид

1

=

1

(cos(0 −ψ )+ isin(0 −ψ )),

ρ

z

z−1 =

1

= ρ−1(cos(− ψ)+ i sin(− ψ)),

(2.24)

z

откуда

1

−1, arg z−1 = −arg z ,

z−1

=

z

т.е. модуль комплексного числа z−1 , обратного числу z , равен обратной величине модуля числа z , а его главное значение аргумента отличается от главного аргумента числа z только знаком.

41

Возведение в степень
Переходим	к вопросу	о	возведении в	степень	комплексного	числа
z = r(cosϕ + isinϕ) ,	заданного	в	тригонометрической		форме. Если	n -
натуральное число, то с помощью формулы (2.21)				получаем формулу
(r(cosϕ +i sinϕ))n = r n (cosnϕ + i sin nϕ) .						(2.25)

Следовательно, при возведении комплексного числа в степень модуль возводится в ту же степень, а аргумент умножается на показатель степени.

Формула (2.25) будет верной и для целых отрицательных показателей.

Поскольку zn = (z−1 )n , то достаточно использовать эту формулу для числа z−1 , тригонометрическая форма которого определена формулой (2.24).

Формулу (2.25) называют формулой Муавра. Отметим частный случай этой формулы при r =1

(cosϕ + i sinϕ )n = cos nϕ + i sinnϕ.

(2.26)

Формула (2.26) имеет большое практическое приложение. Так частным случаем формулы Муавра (2.26) удобно пользоваться при выведении тригонометрических формул синуса и косинуса кратных углов.

НапримерU ,U выведем формулу синуса и косинуса двойного аргумента. Используя (2.26) при n = 2. Имеем

(cosϕ + isinϕ)2 = cos 2ϕ + isin 2ϕ ,

cos2 ϕ + 2isinϕcosϕ + i2 sin2 ϕ = cos2ϕ + isin 2ϕ, (cos2 ϕ −sin2 ϕ)+ (2sinϕcosϕ)i = cos2ϕ + isin 2ϕ .

Приравнивая действительные и мнимые части комплексных чисел, записанных справа и слева от знака равенства, имеем

cos2ϕ = cos2 ϕ −sin2 ϕ , sin 2ϕ = 2sinϕcosϕ .

Извлечение корня п-ой степени
Пусть нужно извлечь корень п-ой степени из числа	z = r(cosϕ + isinϕ) .
Предположим, что это сделать можно и что в результате	получается число
ρ(cosψ + isinψ ) , т.е.
[ρ(cosψ + isinψ )]n = r(cosϕ + isinϕ).	(2.27)

Применим формулу Муавра к левой части равенства (2.27), имеем

ρn (cos nψ + isin nψ ) = r(cosϕ + isinϕ)

Т.к. два комплексных числа равны только в случае, если их модули равны, то ρn = r ρ = n r .

А так как аргументы равных комплексных чисел отличаются на 2πk , k Z , то

42

nψ =ϕ + 2πk ψ =	ϕ + 2πk .
Давая k различные	n
	значения, получим различные значения искомого
корня. Действительно, при
k = 0, 1, 2, ..., n −1

мы получим п значений корня, которые все будут различными, так как

увеличение k на единицу влечет за собой увеличение аргумента на									2π	.
Итак, если z = r(cosϕ + isinϕ) , то									n
				ϕ + 2πk	+ i sin		ϕ + 2πk		(2.28)
n z = n r cos				n			n	,
где k =		(т.е. от нуля до n −1).							(*)
	0, n −1
Пусть теперь k произвольно. Если k = nq + r , 0 ≤ r ≤ n −1, то
ϕ + 2kπ =			ϕ + 2(nq + r)π			= ϕ + 2rπ		+ 2qπ ,
	n			n			n

т.е. значение аргумента при нашем k отличается от значения аргумента при k = r на число, кратное 2π ; мы получаем, следовательно, такое же значение корня, как и при k , равном r , т.е. входящем в систему (*).

Таким образом, извлечение корня п-ой степени из комплексного числа z всегда возможно и дает п различных значений. Все значения корня п-ой степени

расположены на окружности радиуса n z с центром в нуле и делят эту

окружность на п равных частей.

Отметим, что корень п-ой степени из действительного числа z также имеет п различных значений; действительных среди этих значений будет два, одно или ни одного, в зависимости от знака z и четности п, остальные значения будут комплексными. Корень п-ой степени из нуля имеет только одно значение,

равное нулю, т.е.

n 0 = 0 .

НапримерU

,U найдем значения кубического корня из числа − 8.

Решение.

Представим заданное число

в тригонометрической форме

−8 =8(cosπ + isinπ )

и применим формулу (2.28).

π

+ 2kπ

+ isin

π + 2kπ

3 −8 = 3 8(cosπ + isinπ )= 2 cos

3

3

, k = 0, 1, 2 .

Подставляя

последовательно

k =

,

получим

соответственно три

0; 2

значения кубического корня из − 8.

z

π

+ isin

π

0

= 2 cos

3

3

=1 + i 3 ;

z1 = 2(cosπ + isin π )

= −2 ;

z

5π

+ isin

5π

3 .

2

= 2 cos

3

=1 − i

3

43

На этом примере мы убедились, что одно значение корня – действительное число, два других – комплексные.

2.4 Корни из единицы

Особенно важен случай извлечения корня п-ой степени из числа 1. Этот корень имеет п значений, причем, ввиду равенства 1 = cos0 + isin 0 и формулы (2.28) все эти значения или, как мы будем говорить, все корни п-ой степени из единицы, задаются формулой

n 1 = cos	2kπ	+ isin	2kπ	; k = 0, 1, ..., n −1.	(2.29)
	n		n

Действительные значения корня п-ой степени из единицы получаются при значениях k = 0 и n2 , если п четно, и при k = 0, если п нечетно. На комплексной

плоскости корни п-ой степени из единицы расположены на окружности единичного круга и делят ее на п равных дуг; одной из точек деления служит действительное число 1. Отсюда следует, что те из корней п-ой степени из единицы, которые не являются действительными, расположены симметрично относительно действительной оси, т.е. попарно сопряжены.

Квадратный корень из единицы имеет два значения: 1 и – 1, корень четвертой степени из единицы – четыре значения: 1, - 1, i и −i . Для дальнейшего полезно запомнить значение кубического корня из единицы. Это будут, ввиду

(2.29), числа cos 2k3π + isin 2k3π , где k = 0, 1, 2 , т.е., кроме самой единицы, также сопряженные между собой числа

ε1 = cos		2k	+ isin		2k		= −	1		+ i		3
														,
		3				3		2				2					(2.30)
ε2	= cos	4π	+ isin			4π	= −		1		− i		3
		3				3			2			2			.
СправедливыU				следующие утверждения													z можно
1	Все значения корня									п-ой			степени			из комплексного числа

получить умножением одного из этих значений на все корни п-ой степени из единицы.

	Действительно, пусть z1 будет одним из значений корня п-ой степени из
числа z , т.е. zn = z , а ε				- произвольное значение корня п-ой степени из единицы,
	1		(z ε)n
т.е.	ε n =1. Тогда			= znε n = z ,	т.е. z ε также будет одним из значений для
n z .			1	1	1
	Умножая z		на каждый из корней п-ой степени из единицы, получим все
		1
значения корня числа z .
	ПримерыU	.U 1) Одно из значений кубичного корня из – 8 есть – 2. Два других
будут, ввиду (2.30) числа − 2ε1 =1 − i					3 и − 2ε2 =1 + i 3 .
	2) 4 81 имеет четыре значения: 3; – 3, 3i , − 3i .

44

2 Произведение двух корней п-й степени из единицы само есть корень п-ой степени из единицы.

Действительно, если ε n =1 и ηn =1, то (εη)n =ε nηn =1.

3 Число, обратное корню п-ой степени из единицы, само является корнем п-ой степени из единицы.

В самом деле, пусть ε n =1. Тогда из ε ε −1 =1 следует εn (ε−1 )n =1, т.е.

(ε −1 )n =1.

Таким образом обобщив сказанное, получим

Всякая степень корня п-ой степени из единицы есть также корень п- ой степени из единицы.

Всякий корень k -ой степени из единицы будет также корнем l -ой степени из единицы для всякого l , кратного k .

Отсюда следует, что если мы будем рассматривать всю совокупность корней п-ой степени из единицы, то некоторые из этих корней уже будут корнями n′-ой степени из единицы для некоторых n′, являющихся делителями числа n . Однако, для всякого n существуют, такие корни n -ой степени из единицы, которые не являются корнями из единицы никакой меньшей степени. Такие корни называются первообразными корнями n -ой степени из единицы. Их существование вытекает из формулы (2.29): если значение корня, соответствующее данному значению k , мы обозначим через εk (так чтоε0 =1), то

на основании формулы Муавра имеем

ε1k =εk .							(2.31)
Никакая степень числа ε1 , меньшая, чем n -я, не будет, следовательно,
равна 1, т.е. ε1 = cos	2π	+ isin		2π	является первообразным корнем.
				n
	n
Корень n -ой степени					из единицы ε тогда и только	тогда	будет
первообразным, если его степени εk , k = 0, 1, ..., n −1, различны,						т.е. если ими
исчерпываются все корни степени из единицы.
Действительно, если все указанные степени числа ε различны, то ε							будет,
очевидно, первообразным корнем n -ой степени. Если же, например, ε k =εl								при
0 ≤ k ≤ l ≤ n −1, то εl−k =1,			т.е., ввиду неравенств 1 ≤ l − k ≤ n −1,			корень	ε	не
будет первообразным.

Число ε1 , найденное выше, в общем случае – не единственный

первообразный корень n -ой степени. Для разыскания всех этих корней пользуются следующей Uтеоремой.U

Если ε есть первообразный корень n -ой степени из единицы, то число

εk тогда и только тогда будет первообразным корнем n -ой степени, если k взаимно просто с n .

В самом деле, пусть d будет наибольшим общим делителем чисел k и n . Если d >1 и k = dk′, n = dn′, то

(ε k )n′ =ε kn′ =ε k′n = (ε n )k′ =1,

45

т.е. корень εk оказался корнем n′-й степени из единицы.

Пусть, с другой стороны, d =1 и пусть, вместе с тем, число εk оказывается корнем m -й степени из единицы, 1 ≤ m < n . Таким образом,

(ε k )m =ε km =1.

Так как число ε - первообразный корень n -ой степени из единицы, т.е. лишь его степени с показателями, кратными n , могут быть равными единице, то число km будет кратным n . Отсюда вытекает, однако, так как 1 ≤ m < n , что числа k и n не могут быть взаимно простыми в противоречие с предположением.

Таким образом, число первообразных корней n -ой степени из единицы равно числу целых положительных чисел k , меньше n и взаимно простых с ним. Выражение для этого числа, обычно обозначаемого через ϕ(n) , можно найти

в любом курсе теории чисел.

Если p - простое число, то первообразными корнями p -й степени из

единицы будут все эти корни, кроме самой единицы. С другой стороны, среди

корней четвертой степени из единицы первообразными будут i и −i , но не 1 и

−1.

2.5 Показательная и логарифмическая функции комплексной переменной

Определение показательной функции

Исследованием показательной и логарифмической функций комплексного переменного Вы займетесь в курсе математического анализа и теории функций комплексного переменного, здесь же, ознакомимся лишь с важными, с точки зрения алгебры, сведениями.

Так Эйлер дал разумное определение показательной функции с основанием e , именно

ea +bi = ea (cosb + isin b).

(2.32)

Математический анализ предоставляет очень много доводов в пользу разумности и целесообразности такого определения, которые мы опускаем.

Формулы Эйлера

Положим в определении показательной функции a = 0. Получим: cosb + isin b = ebi .

Заменив b на − b , получаем cosb − isin b = e−bi .

Складывая и вычитая почленно эти равенства, найдем формулы

	cosb =	ebi + e−bi	,	sin b =	ebi − e−bi	,	(2.33)
		2			2i

носящие название формул Эйлера. Формулы Эйлера устанавливают связь между тригонометрическими функциями и показательной с мнимыми показателями.

46

Натуральный логарифм комплексного числа
Комплексное	число, заданное	в	тригонометрической	форме
z = r(cosϕ + isinϕ) ,	можно записать в	форме	z = reϕi . Эта форма	записи

комплексного числа называется показательной. Она сохраняет все хорошие свойства тригонометрической формы, но еще более кратка.

Далее, т.к. z = reϕi , а eln r eϕi = eln r +ϕi , то естественно считать, что

ln z = ln r +ϕi ,

(2.34)

т.е вещественной частью логарифма комплексного числа, оказывается, является логарифм его модуля, мнимой частью – его аргумент.

Это в некоторой степени объясняет «логарифмическое» свойство аргумента – аргумент произведения равен сумме аргументов множителей.

Введенная таким образом логарифмическая функция определена для всех комплексных чисел, за исключением нуля. Необходимо только помнить, что логарифмическая функция многозначна, в силу многозначности аргумента. Однозначность можно было бы установить, например, выбирая ветвь логарифма, для которой −π <ϕ ≤π , но это приводит к ряду неудобств. В частности, свойство логарифма – логарифм произведения равен сумме логарифмов сомножителей – верно лишь с учетом многозначности. Так, например, один из значений ln1

является 0, одним из значений ln(−1)

является

πi , ибо

−1 = cosπ + isin π = eπi .

Однако

ln[(−1) (−1)]=πi + πi = 2πi . Это одно из значений логарифма 1 (ибо

1 = cos 2kπ + isin 2kπ ), но отличное от 0.

Показательная функция с произвольным основанием

Пусть z - комплексное число, отличное от нуля. Тогда z = eln z

при любом

значении ln z . Поэтому естественно считать по определению

z w = ew ln z .

(2.35)

Это снова многозначная функция от

z , в силу многозначности ln z , который

определен с точностью до слагаемого 2kπi .

Посмотрим,

напримерU

,U чему равно ii . Используя формулу (2.35), имеем

ii = ei ln i

(в нашем случае z =i ,

w =i ). Находим

π

+ 2kπ

lni = i

. Таким образом

2

π

π

+2

π

π

i i

+2πk

−

πk

как

−

+2kπ

Результат

ii = e 2

= e

2

Так

lni = i

2

+ 2kπ ii

= e 2

.

кажется несколько парадоксальным – все значения «очень мнимого» выражения ii вещественны.

47

2.6 Вопросы для самоконтроля

1Сформулируйте определение комплексного числа.

2Какое комплексное число называется чисто мнимым?

3Что означает алгебраическая форма записи комплексного числа?

4Какие два комплексных числа называются противоположными?

5Объясните, что значит сложить комплексные числа, заданные в алгебраической форме; умножить комплексное число на действительное.

6Объясните принцип деления комплексных чисел, заданных в алгебраической форме.

7Какое комплексное число называется сопряженным данному?

8Запишите в общем виде целые степени мнимой единицы.

9Что означает возведение комплексного числа, заданного алгебраической формой в степень n ( n - натуральное число)?

10Выведите формулы для извлечения квадратного корня из комплексного числа, заданного в алгебраической форме.

11Расскажите как изображаются комплексные числа на плоскости (в частности чисто мнимые, действительные); определите при этом операции сложения, вычитания, умножения на действительное число.

12Объясните какая система координат называется полярной и как в этом случае определяются координаты любой точки плоскости.

13Какая форма записи называется тригонометрической формой комплексных чисел?

14Запишите формулы, связывающие алгебраическую и тригонометрическую формы записи комплексных чисел.

15Какой аргумент комплексного числа называется главным?

16Сформулируйте правило умножения комплексных чисел, записанных

втригонометрической форме.

17Сформулируйте правило нахождения частного двух комплексных чисел, заданных в тригонометрической форме.

18Сформулируйте правило возведения в степени комплексных чисел, заданных в тригонометрической форме.

19Сформулируйте правило извлечения корня n -ой степени из комплексного числа, заданного в тригонометрической форме.

20Расскажите о значении корня n -ой степени из единицы и о сфере его применения.

21Какие корни называются первообразными корнями n -й степени из

единицы?

22В каком случае корень n -й степени будет первообразным?

23Чему равно число первообразных корней n -й степени из единицы?

24Запишите формулы Эйлера.

25Какая форма записи комплексного числа называется показательной?

48