Глава 7 Аналитическая геометрия на плоскости

7.1 Аффинная и прямоугольная декартовы системы координат. Простейшие задачи

Пусть на плоскости даны точка O и базис {e1 , e2 }.

Совокупность точки O и базиса {e1 , e2 } называется аффинной системой координат на плоскости (или аффинным репером), и обозначается R (O; e1 , e2 ) или Oxy (рисунок 35).

Точка O называется началом координат. Ось, проходящая через точку O и имеющая направление вектора e1 , называется осью Ox или осью абсцисс.

Рисунок 35

Ось, проходящая через точку O и имеющая направление вектора e2 , называется осью Oy или осью ординат.

Пусть на плоскости задан аффинный репер R (O; e1 , e2 ) и любая точка M .

Рассмотрим OM - радиус-вектор точки M и пусть OM = xe1 + ye2 . Координатами точки M относительно аффинного репера R (O; e1 , e2 )

называются координаты радиус-вектора этой точки относительно базиса {e1 , e2 }.

Пишут: M (x, y)R .

Аффинная система координат на плоскости позволяет решать ряд простейших задач. Рассмотрим три из них.

Нахождение координат вектора, заданного координатами начала и

конца

		Пусть в пространстве	заданы аффинный репер			R (O; e1 , e2 ) и точки
A(x1,	y1 )R , B(x2 , y2 )R . Найдем		координаты вектора			относительно базиса
				AB
{e , e	2	}.
1

Чтобы получить координаты вектора, нужно из координат его конца вычесть соответствующие координаты начала, то есть

	={x2	− x1 ; y2	− y1	}{e , e }.		(7.1)
AB
				1	2

152

Задача о деление отрезка в заданном отношении

Точка M , принадлежащая прямой M1M 2 , делит отрезок M1M 2 в отношении λ (λ ≠ −1) (рисунок 36), если выполняется векторное равенство:

M1M = λMM2 .

Рисунок 36

Если λ > 0 , то

↑↑

и говорят, что точка M делит отрезок M1M 2

M1M

MM2

внутренним образом в отношении λ .

Если λ < 0 , то

↑↓

и точка M лежит вне отрезка M1M 2 , но на

M1M

MM2

прямой M1M 2 , тогда говорят, что

точка M делит

отрезок

M1M 2 внешним

образом в отношении λ .

R (O; e1 , e2 ) даны

Пусть

относительно

аффинного

репера

точки

M1(x1, y1 )R ,

M 2 (x2 ,

y2 )R . Найдем координаты точки

M , которая делит отрезок

M1M 2 в отношении λ :

x =

x1 + λx2

;

y =

y1 + λy2

.

(7.2)

1 + λ

1 + λ

(то

есть точка M -

середина

отрезка

M1M 2 ),

В частности,

при λ =1

имеем:

x

+ x

2

x =

1

2

- формулы для нахождения координат середины отрезка.

y1 + y2

y =

2

Например, пусть даны две точки M1(−1,−2), M2 (3,4). На прямой M1M 2

найдем точку М, которая в три раза ближе к M1 , чем к M 2

и находится вне

отрезка M1M 2 , а также найдем середину этого отрезка.

Решение. Искомая точка М делит отрезок M1M 2 в отношении λ = −1 . По

формулам (7.2), считая x1 = −1, y1 = −2, x2 = 3, y2 = 4

находим

3

1

1

−1 +

−

3

− 2

+

−

4

3

3

x =

= −3; y =

= −5,

1

1

+

−

1 +

−

1

3

3

153

Таким образом, M (−3,−5) .

С помощью формул для нахождения координат середины отрезка находим точку N –середину отрезка M1M 2

x = −12+ 3 =1; y = − 22+ 4 =1,

Следовательно, N(1,1) - середина M1M 2 .

Совокупность точки O и ортонормированного базиса {i ; j} называется

прямоугольной декартовой системой координат на плоскости (или ортонормированным репером). Обозначается R (O; i , j) (рисунок 37).

Рисунок 37

Очевидно, что прямоугольная декартова система координат является частным случаем аффинной системы координат, поэтому рассмотренные выше определения и простейшие задачи справедливы и в прямоугольной декартовой системе координат.

Нахождение расстояния между двумя точками

Пусть относительно R (O; i , j) заданы точки A(x1, y1 )R и B(x2 , y2 )R , тогда расстояние от точки A до точки B находится по формуле

ρ(A; B)=	(x	2	− x )2	+ (y	2	− y	1	)2 .	(7.3)
			1

7.2 Полярная система координат

При рассмотрении свойств некоторых геометрических фигур иногда используют системы координат отличные от аффинной системы координат и ее частных случаев. Одной из таких систем координат является полярная система координат.

Полярной осью называется луч с заданным сонаправленным единичным вектором.

Совокупность точки О (полюса), полярной оси с началом в этой точке и единичным вектором е называется полярной системой координат.

Зададим на плоскости полярную систему координат с началом в точке О (рисунок 38). Тогда каждой точке М плоскости за исключением точки О ставится

154

в соответствие два числа: ρ = ОМ и ϕ = (e, OM ) , которые называются

полярными координатами.

Рисунок 38

Значения ρ, ϕ изменяются в пределах: 0 < ρ < ∞, −π <ϕ ≤π .

И наоборот, каждой паре чисел (ρ,ϕ) , где 0 < ρ < ∞, −π <ϕ ≤π , отвечает

единственная точка плоскости.

Зададим на плоскости дополнительно прямоугольную декартову систему координат R(O, i , j) . Совместим начало обеих систем координат и направим ось

абсцисс по направлению полярной оси.

Каждая точка плоскости будет иметь в этом случае одновременно прямоугольные декартовы и полярные координаты (рисунок 39)

Рисунок 39

Имеем ОМ = xi + yj . Умножим правую и левую части этого равенства на вектора i , j , учтем при этом, что i = e , тогда получаем:

x = OM e = OM e cos(OM ,e) = ρcosα ,

y =OM j = OM j cos(OM , j) = ρcos(900 −α) = ρsinα .

Следовательно, если известны полярные координаты точки, то

	соответствующие прямоугольные декартовы координаты находятся по формулам
	x = ρcosα,	(7.4)
	y = ρsinα.
	Несложно решается обратная задача. Пусть известны прямоугольные

155

декартовы координаты точки M (x, y) , найдем ее полярные координаты. Так как

ρ = OM и ОМ = xi + yj , то

ρ = x2 + y 2 .							(7.5)
Учитывая предыдущие формулы, получаем:
cosα = x =	x	, sin α =	y	=	y	,	(7.6)
ρ	x2 + y 2		ρ		x2 + y 2

откуда однозначно находится значение α , удовлетворяющее условиям

−π <α ≤π .

Например, найдем декартовы координаты точки М, полярные координаты

которой 5, 23π .

Решение. По формулам (7.4) вычисляем:

x = ρ cosα = 5 cos	2π	= −	5	,
	3		2
y = ρ sin α = 5 sin	2π	= 5	3 .
	3	2
						5		5	3
					−		,
Декартовы координаты точки М таковы:						2		2		.

7.3 Преобразование системы координат

При решении многих задач аналитической геометрии наряду с данной прямоугольной системой координат приходится вводить и другие прямоугольные системы координат. При этом, естественно, изменяются как координаты точек, так и уравнения линий. Возникает задача: как, зная координаты точки в одной системе координат, найти координаты этой же точки в другой системе координат. Решить эту задачу позволяют формулы преобразования координат.

Рассмотрим два вида преобразований координат.

Параллельный перенос осей координат

Пусть на плоскости задана прямоугольная система координат Оху. Под

параллельным переносом осей координат понимают переход от системы координат Оху к новой системе О1х1 у1, при этом меняется положение начала

координат, а направление осей и масштаб остаются неизменными.

Пусть начало новой системы координат точка О1 имеет координаты (х0 , у0 ) в старой системе координат Оху, т.е. О1(х0 , у0 ). Обозначим координаты произвольной точки М плоскости в системе Оху через (х, у), а в новой системе О1х1 у1 через (х′, у′) (рисунок 40).

156

Рисунок 40

Рассмотрим векторы

OM = xi + yj, OO1 = x0i + y0 j, O1M = x′i + y′j.

Так как OM =OO1 +O1M , то xi + yj = x0i + y0 j + x′i + y′j , т.е.

xi + yj =(x0 + x′)i +(y0 + y′) j .

Следовательно,

x = x0 + x′,y = y0 + y′.

Полученные формулы позволяют находить старые координаты известным новым x′, y′ и наоборот.

(7.7)

x, y по

Поворот осей координат

Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными.

Пусть новая система О1х1 у1 получена поворотом системы Охуна угол α. Пусть М – произвольная точка плоскости (х, у) - ее координаты в старой

системе и (х′, у′) - в новой системе.

Введем две полярные системы координат с общим полюсом О и полярными осями Ох и Ох1 (масштаб одинаков). Полярный радиус ρ в обеих

системах одинаков, а полярные углы соответственно равны α +ϕ и ϕ, где ϕ - полярный угол в новой полярной системе (рисунок 41)

157

Рисунок 41

По формулам перехода от полярных координат к прямоугольным имеем

x =ρcos(α+ϕ),	x =ρcosϕcosα−ρsinϕsinα,
	т.е.
y =ρsin(α+ϕ),	y =ρcosϕsinα+ρsinϕcosα.

		′		′	. Поэтому
Но ρcosϕ = x ,			ρsinϕ = y
	′	′
x = x cosα− y sinα,					(7.8)
	′	′
y = x sinα+ y cosα.
Полученные формулы называются формулами поворота осей. Они
позволяют	определить		′	старые координаты x, y произвольной точки М через
		′		этой же точки М, и наоборот.
новые координаты x , y

Если новая система координат О1х1 у1 получается из старой Оху путем параллельного переноса осей координат и последующим поворотом осей на угол

α (рисунок 42), то путем			введения вспомогательной системы О1х1′у1′ легко
получить формулы
	′	′	,
x = x cosα− y sinα+ х0				(7.9)
	′	′	,
y = x sinα+ y cosα+ у0

выражающие старые координаты x, y произвольной точки через ее новые координаты x′, y′.

Рисунок 42

158

7.4 Уравнение линии на плоскости

Уравнением линии на плоскости в заданной системе координат Oxy

называется уравнение с двумя неизвестнымиF(x, y) = 0 , которому удовлетворяют

координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты точек, не лежащих на ней.

Входящие в уравнение F(x, y) = 0 координаты x и y произвольной линии

называются текущими координатами.

Для составления уравнения линии следует взять на ней произвольную точку и, исходя из свойств линии, установить зависимость между координатами точек.

Понятие уравнения линии дает возможность решать геометрические задачи алгебраическими методами. Например, задача нахождения точек

пересечения линий, определяемых уравнениями x + y = 0, x 2 + y 2 =1, сводится к

алгебраической задаче решения системы этих уравнений. Рассмотрим примеры линий:

1 x − y = 0 . Переписав это уравнение в виде x = y , заключаем что

множество точек, координаты которых удовлетворяют этому уравнению лежат на биссектрисе I – III координатных углов.

2	x 2 − y 2 = 0 .		Представив уравнение			в виде (x − y)(x + y) = 0 , что
равносильно		x − y = 0,	или	x = y,	, получим x 2	− y 2 = 0 - уравнение биссектрис
		x + y = 0.		x = −y.

всех координатных углов (рисунок 43)

Рисунок 43

3 x 2 + y 2 = 0 . Этому уравнению удовлетворяет лишь точка (0,0) . В данном случае говорят, что уравнение x 2 + y 2 = 0 определяет вырожденную линию.

4 x 2 + y 2 +1 = 0 . Перепишем уравнение в видеx 2 + y 2 = −1, которое означает что нет ни одной точки ему удовлетворяющей. Таким образом,

уравнение	x 2 + y 2 +1 = 0 никакого	геометрического	образа	на плоскости не
определяет.	Линия на плоскости может определятся уравнением вида F (ρ,ϕ) = 0 ,
5
где (ρ,ϕ)	- полярные координаты	точки. Например,	пусть	задано уравнение

159

ρ = a cosϕ , где a - положительной число, переменныеρ,ϕ - полярные координаты. Определим линию задаваемую этим уравнением. Пусть M (ρ,ϕ) - точка удовлетворяющая этому уравнению и точка А с координатами (a,0) - некоторая фиксированная точка (рисунок 44)

Рисунок 44

Если ρ = a cosϕ , где 0 <ϕ <π / 2 , то угол ОМА - прямой (по свойству

прямоугольного треугольника – гипотенуза есть произведение прилежащего катета на косинус угла между ними), но если угол ОМА прямой, то треугольник ОМА является вписанным в окружность (опирающимся на диаметр ОА). Следовательно, множество точек, полярные координаты которых удовлетворяют уравнению ρ = a cosϕ есть окружность с диаметром a .

Итак, по заданному уравнению мы определили в примерах 1-5 линию как геометрическое множество точек ему удовлетворяющих.

Рассмотрим обратную задачу.

Например, выведем уравнение (в заданной прямоугольной системе координат) множества точек, каждая из которых отстоит от точки С(a, b) на

расстоянии R .

Решение. Исходя из условия определяем, что наша задача вывести уравнение окружности радиуса R с центром в точке С(a, b) (рисунок 45).

Рисунок 45

Расстояние от произвольной точки M (x, y) до точки С(a, b) вычисляется по формуле

МС = (x − a)2 + ( y − b)2

160

Если точка M (x, y) лежит на окружности, то МС = R . Таким образом,

R = (x − a)2 + ( y − b)2

или
R 2 = (x − a) 2 + ( y − b)2	(7.10)
Если же точка, например, M1 (x, y) не лежит на окружности,	то		М1С		≠ R
или М1С2 ≠ R 2 , то есть координаты точки М не удовлетворяют уравнению
(7.10). Таким образом, искомое уравнение окружности имеет вид
R 2 = (x − a) 2 + ( y − b) 2
В частности, если a = 0, b = 0 , то есть центр окружности	совпадает с
началом координат, то есть
x 2 + y 2 = R 2 .

Если в уравнение линии переменные входят только в первой степени, то такая линия называется линией первого порядка. К линиям второго порядка

относятся такие линии, уравнения которых в прямоугольной системе координат являются уравнениями второй степени. К линиям первого порядка относятся прямые, второго порядка – эллипс, гипербола, парабола.

Линию на плоскости также можно задать при помощи уравнений:

x = x(t),

y = y(t),

где x и y – координаты произвольной точки M(x, y), лежащей на данной линии, а t

– переменная, называемая параметром. Параметр t определяет положение точки (x,y) на плоскости.

Например, если x=t+1, y=t², то значению параметра, равному двум, соответствует на плоскости точка (3,4), т.к. x=2+1=3, y=2²=4.

Если параметр t изменяется, то точка на плоскости перемещается, описывая данную линию. Такой способ задания линий называется

параметрическим, а уравнения – параметрическими уравнениями линий.

Чтобы перейти от параметрических уравнений к уравнениям вида F(x,y)=0, надо каким-либо способом из двух заданных уравнений исключить параметр t.

Например, из уравнений x = t	, путём подстановки t = x во второе уравнение,
y = t 2

легко получить уравнение у = х2 ; или уравнение вида у − х2 = 0 , т.е.вида

F(x,y)=0. Однако заметим, такой переход не всегда целесообразен и не всегда возможен.

161

7.5 Линии первого порядка на плоскости

1 Уравнение прямой с угловым коэффициентом

Пусть дана некоторая прямая с заданным углом наклона к оси Ox угол α , причем 0 ≤α <π (рисунок 46)

Тангенс угла наклона прямой к оси Ох называется угловым

коэффициентом этой прямой и обозначается k
k = tqα .	(7.11)

Рисунок 46

Выведем уравнение прямой, если известны ее угловой коэффициент k и величина b- длина отрезка ОВ отсекаемого данной прямой на оси Оу (рисунок 46).

Пусть M (x, y) - произвольная точка искомой прямой. Выполним

построение – из точки М проведем прямую параллельную оси Оу, а из точки В - параллельную оси Ох. Полученный, таким образом, треугольник BNM - прямоугольный, углы MBN и MDK равны как соответственные. По определению тангенса острого угла прямоугольного треугольника, имеем

tqα = MNBN ,

но MN=KM-KN=KM-OB=y-b, а BN=x и k = tqα (по условию)

Таким образом, имеем

k =	y − b
	x
или y − b = kx
y = kx +b .			(7.12)
Уравнение (7.12) называется уравнением прямой с угловым
коэффициентом.
Если k = 0			(т.е. tqα = 0 α = 0 ), то прямая параллельна оси Ox и имеет

уравнение y = b .

Таким образом, любая прямая не перпендикулярная оси Ox имеет уравнение вида (7.12). Верно и обратное: любое уравнение вида (7.12) определяет прямую, которая имеет угловой коэффициент k и отсекает на оси Oy отрезок величиной b.

162

2 Уравнение прямой, проходящей через данную точку, с данным угловым коэффициентом

Пусть требуется составить уравнение прямой, зная одну ее точку M1 (x1 , y1 ) и угловой коэффициент k . Запишем уравнение искомой прямой в виде

(7.12) y = kx + b , где b пока неизвестное число. Так как прямая проходит через точку M1 (x1 , y1 ) , то координаты этой точки удовлетворяют уравнению (7.12), то

есть y1 = kx1 + b , откуда находим b = y1 − kx1	и подставляем в исходное
уравнение:
y = kx + ( y1 − kx1 )
или
y − y1 = k( x − x1 ),	(7.13)

- уравнение прямой проходящей через точку M1 (x1 , y1 ) имеющей угловой

коэффициент k .

Например, составим уравнение прямой, проходящей через точку А(2,−1) и образующей с осью Ох угол 450 .

Решение. Так как k = tg 450 =1, то, использовав уравнение (7.13), получим y − (−1) =1(x − 2) , или x − y = 3.

Итак, y = x − 3 - уравнение искомой прямой.

3 Уравнение прямой, проходящей через две заданные точки

Пусть M1 (x1 , y1 ) и M 2 (x2 , y2 ) - две заданные точки через которые проходит искомая прямая, тогда поскольку точка M1 (x1 , y1 ) принадлежит искомой прямой, то на основе формулы (7.13) имеем

y − y1 = k(x − x1 ) .

(7.14)

Но уравнению (7.14) удовлетворяет и точка M 2 (x2 , y2 ) , следовательно

y2 − y1 = k(x2 − x1 ) .

Откуда находим k

k =

y2 − y1

.

x

2

− x

1

Таким

образом, уравнение искомой

прямой, проходящей через точки

M1 (x1 , y1 ) и M 2 (x2 , y2 ) , имеет вид

y − y =

y2 − y1

(x − x )

1

x

1

или

2 − x1

y − y1

=

x − x1

.

(7.15)

y

2

− y

2

x

2

− x

1

- уравнение прямой, проходящей через две заданные точки.

163

4 Угол между двумя прямыми
Рассмотри две прямые L1 : y = k1 x + b1 ,	где	k1 = tgα1 и L2 : y = k2 x + b2 ,
где k2 = tgα2 . Поставим задачу: найти угол	ϕ	между прямыми L1 , L2 . Из

геометрических соображений устанавливаем зависимость между углами α1 , α2 и ϕ (рисунок 47)

Рисунок 47

α2 = α1 + ϕ ϕ =α2 −α1 .

Следовательно,

tgα2 − tgα1

tgϕ = tg(α2 − α1 ) =

.

Таким образом,

1 + tgα1tgα2

tgϕ =

k2 − k1

.

(7.16)

1 + k k

2

1

Формула (7.16) определяет один из углов между прямыми L1 , L2 , другой

угол равен π −ϕ .

Например,

найдем

угол

между

прямыми,

заданными

уравнениями

y = 2x −1 и y = x + 3 .

Очевидно k1 = 2, k2 =1, по формуле (7.16) находим угол между прямыми:

tgϕ =

1 − 2

= −

1

.

1 +1 2

3

1

Таким

образом,

тангенс

одного

из углов

равен −

,

а сам

угол

1

1

3

ϕ = arctg

−

=π − arctg

.

3

3

5 Условие параллельности и перпендикулярности двух прямых

Если прямые L1 ,

L2

параллельны,

то ϕ = 0 ,

и tgϕ = 0 . В этом случае

числитель формулы (7.16) равен 0, то есть k2 −k1 = 0 или

k1 = k2 - условие параллельности прямых.

ϕ =π / 2 ,

Если

прямые

L1 , L2

перпендикулярны,

то есть

то

164

π

π

1

α2

=

+ α1 tgα2

= tg

+ α1

tgα2

= −сtgα1 tgα2 = −

, то есть

2

2

tgα1

k2 =− 1 - условие перпендикулярности прямых. k1

6 Общее уравнение прямой

Теорема 7.1 В прямоугольной системе координат любая прямая задается уравнением первой степени

Ax+By+C =0

(7.17)

и обратно, уравнение (7.17) при произвольных коэффициентах А, В, С определяет некоторую прямую в прямоугольной системе координат Оху.

Доказательство. Докажем первое утверждение. Если прямая не перпендикулярна оси Ох, то она имеет уравнение y =kx +b, которое имеет вид (7.17) при A =k, B =−1,C =b. Если прямая перпендикулярна оси Ох, то все ее точки

имеют одинаковые абсциссы, равные а – величине отрезка, отсекаемого на оси Ох (рисунок 48)

Рисунок 48

Уравнение этой прямой имеет вид x =a, то есть является уравнением первой степени вида (7.17), где A=1, B =0,C =−a. Таким образом, первое

утверждение доказано.

Докажем обратное утверждение. Пусть дано уравнение (7.17), причем хотя

бы один из коэффициентов

A, B не равен нулю. Если B ≠0, то (7.17) можно

записать в виде

y =−

A

x −

C

B B

Полагая k =−

A

, b =−

C

, получаем уравнение y =kx +b.

B

B

C

C

Если B =0, A≠0, то (7.17) принимает вид x =−

. Обозначая

−

через а,

A

A

получим x =a, то есть уравнение прямой, перпендикулярной оси Ох, что и требовалось доказать.

165

Уравнение вида Ax+By+C =0 называется общим уравнением прямой.

7 Неполное уравнение первой степени. Уравнение прямой «в

отрезках»			Ax+ By+C =0	является
Рассмотрим три частных случая, когда уравнение
неполным, т.е. какой-то из коэффициентов равен нулю.
1)	C =0; уравнение имеет вид	Ax+ By =0 и	определяет	прямую,
проходящую через начало координат.
2)	B =0 (А≠0); уравнение имеет	вид Ax+C =0	и определяет	прямую,

параллельную оси Оу. Как было показано в теореме 7.1, это уравнение приводится к виду x =а, где а=−С/ А, а - величина отрезка, отсекаемого прямой на оси Ох (рисунок 48). В частности, если а=0, то прямая совпадает с осью Оу. Таким образом, уравнение x =0 определяет ось ординат.

3) A=0, (В≠0); уравнение имеет вид By+C =0 и определяет прямую,

параллельную оси Ох. Этот факт устанавливается аналогично предыдущему случаю. Если положить −С/ В=b, то уравнение принимает вид y =b, где b -

величина отрезка, отсекаемого прямой на оси Оу (рисунок 49). В частности, если b =0, то прямая совпадает с осью Ох. Таким образом, уравнение y =0 определяет

ось абсцисс.

Рисунок 49

Пусть теперь дано уравнение Ax+ By+C =0 при условии, что ни один из коэффициентов А, В, С не равен нулю. Преобразуем его к виду

			x				+	y		=1.
	−C / A							−C / B
Вводя обозначения a =−C / A, b =−C / B, получаем
	x		+	y	=1.					(7.18)
	a			b

Уравнение (7.18) называется уравнением прямой «в отрезках». Числа a, b

являются величинами отрезков, отсекаемого прямой на осях координат. Эта форма уравнения удобна для геометрического построения прямой.

Например, составим для заданной уравнением 5x + 3y −15 = 0 прямой

уравнение «в отрезках» и построим эту прямую. Для данной заданной прямой, имеем

166

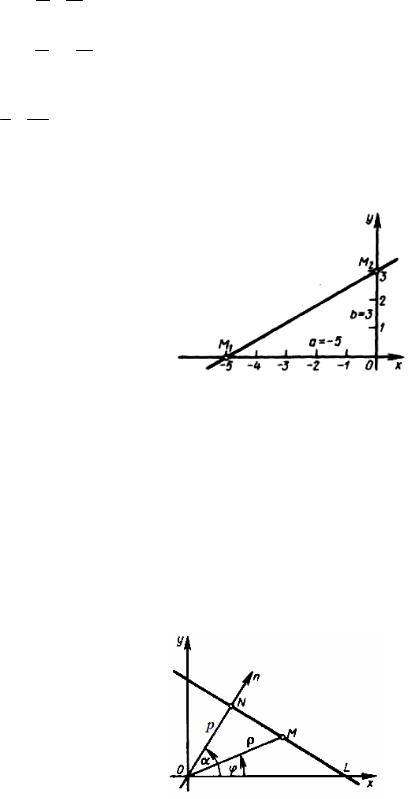
A=5, B =3,C =−15 a =−CA =155 =3,

b =−CB =−153 =−5.

Таким образом, уравнение заданной прямой «в отрезках» имеет вид

3x + −y5 =1.

Чтобы построить эту прямую, отложим на осях координат Ох и Оу отрезки a =3, b =5 и проведем прямую через точки M1(−5,0), M2(0,3) (рисунок 50).

Рисунок 50

8 Уравнение прямой в полярных координатах. Нормальное уравнение прямой

Пусть дана некоторая прямая L. Проведем через начало координат прямую n, перпендикулярную данной, и назовем ее нормалью к прямой L. Буквой N отметим точку, в которой нормаль пересекает прямую L (рисунок 51). На нормали введем направление от точки O к точке N. Таким образом, нормаль станет осью.

Обозначим через α угол, на который нужно повернуть против часовой стрелки ось Ох до совмещения ее положительного направления с направлением нормали, через p - длину отрезка ON.

Рисунок 51

Тем самым, 0 ≤α < 2π, p ≥ 0 . Выведем уравнение данной прямой, считая известными числа α и p. Для этого возьмем на прямой произвольную точку М с

167

полярными координатами (ρ,ϕ) , где О – полюс, Ох – полярная ось. Если точки О и N не совпадают, то из прямоугольного треугольника ONM имеем

p =ρcos(ϕ −α) =ρ(cosαcosϕ +sinαsinϕ).
Это равенство можно переписать в виде
ρcosαcosϕ+ρsinαsinϕ− p =0	(7.19)

Так как точки, не лежащие на данной прямой L, не удовлетворяют уравнению (7.19), то (7.19) - уравнение прямой L в полярных координатах.

Но в силу формул, связывающих прямоугольные и полярные координаты, имеем: ρcosϕ = х, ρsinϕ = y. Таким образом, уравнение (7.19) в прямоугольной

системе координат примет вид
xcosα+ ysinα− p =0.	(7.20)

Если точки О и N совпадают, то прямая L проходит через начало координат и p =0.

В этом случае, очевидно, для любой точки М прямой L выполняется равенство cos(ϕ −α) =0. Умножая его на ρ , получаем ρcos(ϕ −α) =0, откуда

ρcosαcosϕ + ρsinαsinϕ =0 или xcosα+ ysinα=0.

Таким образом, и в этом случае уравнение прямой можно представить в виде (7.20).

Уравнение (7.20) называется нормальным уравнением прямой L.

9 Расстояние от точки до прямой

С помощью нормального уравнения прямой можно определить расстояние от данной точки плоскости до прямой.

Пусть L - прямая, заданная нормальным уравнением:

xcosα+ ysinα− p =0 и пусть M0 (x0 , y0 ) - точка, не лежащая на этой прямой. Требуется найти расстояние d от точки M0 до прямой L.

Через точку M0 проведем прямую L0 параллельно прямой L. Пусть N 0 - точка пересечения L0 с нормалью, p0 - длина отрезка ON 0 (рисунок 52).

		Рисунок 52
Если точки	N и	N 0 лежат по одну сторону от точки О, то нормальное
уравнение прямой	L0	имеет вид xcosα+ ysinα− p0 =0. Так как	точка
M0 (x0 , y0 ) L0, то	x0 cosα+ y0 sinα− p0 =0, откуда x0 cosα+ y0 sinα= p0. В		этом

168

случае

d = p0 − p = x0 cosα+ y0 sinα− p .

Если точки N и N 0 лежат по разные стороны от точки О, то нормальное уравнение прямой L0 имеет вид xcosα1 + y sinα1 − p0 =0, где α1 отличается от α на

π , т.е. α1 =π −α .

Следовательно, p0 = x0 cosα1 + y0 sinα 1=−x0 cosα − y0 sinα. В этом случае

d = p0 + p = x0 cosα+ y0 sinα− p .

Таким образом, в каждом из рассмотренных случаев получаем формулу

расстояния от точки до прямой:

d =		x0 cosα+ y0 sinα− p		.	(7.21)

Из формулы (7.21) следует, что для вычисления расстояния d от точки M0 до прямой L нужно в левую часть нормального уравнения поставить вместо (x, y) координаты точки M0 и полученное число взять по модулю.

Теперь покажем, как привести общее уравнение прямой к нормальному

виду.
Пусть
Ax+ By+C =0	(7.22)
- общее уравнение некоторой прямой, а
xcosα+ ysinα− p =0	(7.23)

- ее нормальное уравнение.

Так как уравнения (7.22) и (7.23) определяют одну и ту же прямую, то их коэффициенты пропорциональны. Умножая все члены уравнения (7.22) на произвольный множитель µ ≠ 0 , получаем уравнение

µ Ax+µBy+µC =0.

При соответствующем выборе µ полученное		уравнение обращается в
уравнение (7.23), т.е. выполняются равенства
µ A=cosα, µB =sinα, µC =−p.		(7.24)
Чтобы найти множитель µ , возведем первые		два из этих равенств в
квадрат и сложим, тогда получаем
µ2 ( A2 + B 2 ) = cos 2 α + sin 2 α =1.
Отсюда	1
µ = ±	A2 + B2 .	(7.25)

Число µ называется нормирующим множителем. Знак нормирующего множителя определяется с помощью третьего из равенств (7.24). Согласно этому равенству µС число отрицательное, если С ≠ 0 . А значит, в формуле (7.25)

берется знак, противоположный знаку С. Если С=0, то знак нормирующего множителя можно выбрать произвольно.

Рассмотрим еще один способ нахождения расстояния от точки до прямой.

169

Пусть прямая L задана уравнением Ax+ By+C =0 и пусть точка не лежит на данной прямой M0 (x0 , y0 ) (рисунок 53). Найдем расстояние от точки M0 до прямой L.

Рисунок 53

Решение. Расстояние d от точки M0 до прямой L рано модулю проекции

вектора М1M0 , где М1(х1, у1) - произвольная точка прямой L, на направление нормального вектора. Следовательно,

d = пр M M		0	= M1M0 n		= ( x0 −x1 )A+( y0 − y1 )B =
n	1			n	A2 +B2
= Ax0 +By0 − Ax1 −By1 .
	A2 +B2
Так как точка М1(х1, у1) принадлежит прямой L, то						Ax1 + By1 +C =0,	т.е.
C =−Ax1 −By1. Поэтому
d = Ax0 +By0 +C .						(7.26)
A2 +B2
Итак, формула	d		выражает расстояние от точки M0 (x0 , y0 ) до прямой				L:
Ax+ By+C =0.
Например, найдем расстояние от точки M0( 2,−1) до прямой 3x +4y −22=0.
Решение. По формуле (7.26), имеем d = 3 2 +4( −1) −22						= 20 =4.
					32 +42	5

Таким образом, расстояние от заданной точки до заданной прямой равно 4 единицам длины.

7.6 Линии второго порядка на плоскости

Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

Ax2 +2Bxy+Cy2 +2Dx+2Ey+F =0.

(7.27)

Коэффициенты уравнения — действительные числа, и по крайней мере одно из чисел А, В, С отлично от нуля. Линии, задаваемые такими уравнениями

170

называются линиями (кривыми) второго порядка. Ниже будет установлено, что уравнение (7.27) определяет на плоскости окружность, эллипс, гиперболу или параболу. Прежде, чем переходить к этому утверждению, изучим свойства перечисленных кривых.

1 Окружность

Простейшей кривой второго порядка является окружность. Напомним, что окружностью радиуса R c центром в точке M0 называется множество всех точек М

плоскости, удовлетворяющих условию M0М = R. Пусть точка M0 в прямоугольной системе координат Оху имеет координаты (х0 , у0 ), а M(х, у) - произвольная точка окружности (рисунок 54)

				Рисунок 54
Тогда из условия M			0	М = R получаем уравнение	( х− х	)2 +( у− у )2	= R,
то есть					0	0
	)2 +( у− у )2	=R2 .
( х− х						(7.29)
0	0

Уравнению (7.29) удовлетворяют координаты любой точки M(х, у) данной

окружности и не удовлетворяют координаты никакой точки, не лежащей на окружности.

Уравнение (7.29) называется каноническим уравнением окружности.

Например, покажем, что уравнение x 2 + y 2 + 2x − 6 y −15 = 0 является

уравнением окружности, и найти ее радиус.

Преобразуем данное уравнение, приведя его к виду (7.29): (x 2 + 2x +1) + ( y 2 − 6 y + 9) −1 − 9 −15 = 0,

(x +1) 2 + ( y − 3) 2 = 25 .

Итак, данное уравнение есть окружность с центром в точке (-1,3) и радиусом 5.

2 Эллипс Эллипсом называется множество всех точек плоскости, сумма

расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

171

Обозначим фокусы через F1 и F2, расстояние между ними через 2с, а

сумму расстояний от произвольной	точки эллипса до	фокусов — через 2а,
(рисунок 55). По определению 2а > 2с, т. е. а> с.
Для вывода уравнения эллипса выберем систему координат Оху так, чтобы
фокусы F1 и F2 лежали на оси Ох,	а начало координат совпадало с серединой
отрезка F1 F2. Тогда фокусы будут	иметь следующие	координаты; F1(−с,0) и
F2(с, 0).

Рисунок 55

Пусть M(х, у) — произвольная точка эллипса. Тогда, согласно определению эллипса, MF1 + MF2 =2a, т. е.

(x +c)2 + y2 + (x −c)2 + y2 =2a

(7.30)

Это, по сути, и есть уравнение эллипса.

Преобразуем уравнение (7.30) к более простому виду следующим образом:

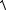(x +c)2 + y2 =2a − (x −c)2 + y2 ,

x2 +2cx+c2 + y2 =4a2 −4a (x −c)2 + y2 + x2 −2cx +c2 + y2 , a (x −c)2 + y2 =a2 −cx,

a2 x2 −2a2cx+a2c2 +a2 y2 =a4 −2a2cx+c2 x2 , (a2 −c2 )x2 +a2 y2 =a2 (a2 −c2 ).

Так как a >c , то a2 −c2 >0. Положим a2 −c2 =b2

Тогда последнее уравнение примет вид b2 x2 +a2 y2 =a2b2 или

	x2	+	y2	=1.	(7.31)
	a2		b2

Можно доказать, что уравнение (7.31) равносильно исходному уравнению.

Уравнение (7.31) называется каноническим уравнением эллипса.

Исследование формы эллипса по его уравнению

Установим форму эллипса, пользуясь его каноническим уравнением.

1 Уравнение (7.31) содержит х и у только в четных степенях, поэтому если

172

точка (х,у) принадлежит эллипсу, то ему также принадлежат точки (х,-у), (-х,у), (-х,-у). Отсюда следует, что эллипс симметричен относительно осей Ох и Оу, а также относительно точки О(0,0), которую называют центром эллипса.

2 Найдем точки пересечения эллипса с осями координат. Положив у=0, находим две точки А1(−а,0) и А2(а,0), в которых ось Ох пересекает эллипс

(рисунок 56). Положив в уравнении (7.31) х=0, находим точки пересечения эллипса с осью Оу: В1(0,−b) и B2 (0,b). Точки А1, A2 , B1, B2 называются вершинами

эллипса. Отрезки А1A2 , B1B2 , а также их длины 2а и 2b называются

соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.

Рисунок 56

3 Из уравнения (7.31) следует, что каждое слагаемое в левой части не

превосходит единицы, т. е. имеют	место неравенства	х2		≤1,	у2
		а	2		2
−a ≤ x ≤a, −b ≤ y ≤b. Следовательно,					b
	все точки эллипса		лежат

прямоугольника, образованного прямыми x =±a, y =±b.

≤1 или внутри

4В уравнении (7.31) сумма неотрицательных слагаемых х2 , у2 равна

а2 b2

единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если |х| возрастает, то |у| уменьшается и наоборот.

Из сказанного следует, что эллипс имеет форму, изображенную на рисунке 56 (овальная замкнутая кривая).

Дополнительные сведения об эллипсе

b

Форма эллипса зависит от отношения а. При b= а эллипс превращается в

окружность, уравнение эллипса (7.31) принимает вид x2 + y2 =a2 .

В качестве характеристики формы эллипса часто пользуются соотношением аc .

Отношение аc половины расстояния между фокусами к большой полуоси

173

эллипса называется эксцентриситетом эллипса и обозначается буквой ε («эпсилон»):

	ε =	c	,	(7.32)
		a

причем 0 <ε <1, так как 0 <c <a. С учетом равенства a2 −c2 =b2 формулу (7.32) можно переписать в виде

ε =	a2 −b2		a2 −b2			b	2
	a	=		a2	=	1−	,
т.е.						a
ε =	b 2		b	= 1	−ε2 .		(7.33)
	1−		a
	a

Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить ε =0, то эллипс превращается в окружность.

Пусть М(х,у) – произвольная точка эллипса с фокусами F1 и F2 (рисунок

57) Длины отрезков	F1М =r1 и F2M =r2 называются фокальными радиусами
точки М. Очевидно,	r1 +r2 =2a.
Имеют места формулы
r1 =a +εx и r2 =a −εx .

Прямые x =±εa называются директрисами эллипса.

	Рисунок 57
	Например, составим каноническое уравнение эллипса, зная, что:
	а) полуоси его a = 6, b = 4 ;
	б) расстояние между фокусами 2c =10 , а большая полуось 2a =16 .				y2
	Решение. а) Каноническое уравнение эллипса имеет вид	x2		+		=1.
		a2			b2

174

Подставляя в него a = 6, b = 4 , получаем x2 + y2 =1. 36 14

б) Из условия 2c =10 следует с = 5 , 2a =16 а = 8.

Чтобы написать уравнение эллипса, необходимо найти малую полуось b. Поскольку между величинами a, b, c у эллипса существует зависимость

a2 −c2 =b2 . В нашем случае b2 =64−25=39, следовательно, уравнение имеет вид

x2 + y2 =1. 64 39

3 Гипербола Гиперболой называется множество всех точек плоскости, модуль

разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Обозначим фокусы через F1 и F2, расстояние между ними через 2с, а

модуль разности расстояний от каждой точки гиперболы до фокусов через 2а. По определению 2а < 2с, т. е. а < с.

Для вывода уравнения гиперболы выберем систему координат Оху так, чтобы фокусы F1 и F2 лежали на оси Ох, а начало координат совпало с серединой

отрезка F1 F2 (рисунок 58)

Рисунок 58

Тогда фокусы имеют координаты F1(−с,0) и F2 (с,0). Пусть М(х,у)

произвольная точка

гиперболы. Тогда согласно определению гиперболы

МF

−

МF

=2a или

МF

−

МF

=±2a, т. е.

1

2

1

2

(x +c)2 + y2 − (x −c)2 + y2 =±2a.

После упрощений, подобным упрощением, используемым при выводе уравнения эллипса, получим каноническое уравнение гиперболы

	x2	−	y2	=1,	(7.34)
	a2		b2

где b2 =c2 −a2 .

175

Исследование формы гиперболы по ее уравнению

Установим форму гиперболы, пользуясь ее каноническим уравнением.

1 Уравнение (7.34) содержит х и у только в четных степенях. Следовательно, гипербола симметрична относительно осей Ох и Оу, а также относительно точки О(0, 0), которую называют центром гиперболы.

2 Найдем точки пересечения гиперболы с осями координат. Положив у=0 в уравнении (7.34), находим две точки пресечения гиперболы с осью Ох: А1(−а,0) и

А (а,0). Положив х=0 в		(7.34), получаем	у2 =−b2	чего быть не		может.
2
Следовательно, гипербола ось Оу не пересекает.
Точки	А1(−а,0) и	А2(а,0) называются	вершинами		гиперболы,	отрезок
А1А2 =2а - действительной осью, отрезок			ОА1 =ОА2 =а — действительной
полуосью гиперболы.					B2 (0,b) называется
Отрезок	В1В2 =2b,	соединяющий точки В1(0,−b)		и

мнимой осью, число b - мнимой полуосью. Прямоугольник со сторонами 2а и 2b

называется основным прямоугольником гиперболы.

3 Из уравнения (7.34) следует, что уменьшаемое х2 не меньше единицы,

а2

т.е. что х2 ≥1 или х ≥а. Это означает, что точки гиперболы расположены справа

а2

от прямой х=а (правая ветвь гиперболы) и слева от прямой х=-а (левая ветвь гиперболы).

4 Из уравнения (7.34) гиперболы очевидно, что если х возрастает, то и у

возрастает.

Из сказанного следует, что гипербола имеет форму, изображенную на рисунке 59 (кривая, состоящая из двух неограниченных ветвей).

y

Рисунок 59

Например, составим каноническое уравнение гиперболы, если расстояние между вершинами ее равно 20, а расстояние между фокусами 30.

Решение. Вершины гиперболы лежат на ее действительной оси. По условию 2а = 20, 2с = 30 . Значит, что а =10, с =15 а2 =100, с2 = 225 .

176

Величины a, b, c у гиперболы связаны соотношением с2 =b2 +a2 , отсюда

b2 =c2 −a2 =225−100=125.

Таким образом, уравнение гиперболы имеет вид

x2 − y2 =1. 100 125

Асимптоты гиперболы

Прямая L называется асимптотой неограниченной кривой К, если расстояние d от точки М кривой К до этой прямой стремится к нулю при неограниченном удалении точки М вдоль кривой К от начала координат. На рисунке 60 приведена иллюстрация понятия асимптоты: прямая L является асимптотой для кривой К.

Рисунок 60

Покажем, что гипербола

x2

−

y2

=1

имеет две асимптоты:

a2

b2

b

b

y =

x,

y =−

x.

(7.35)

a

a

Так как

прямые (7.35) и

гипербола (7.34) симметричны относительно

координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти.

Возьмем на прямой y =		b	x	точку N имеющей ту же абсциссу х, что и
	y = b	a
точка М(х,у) на гиперболе		x2		−а2 (рисунок 61).
	a

177

Рисунок 61

Найдем расстояние MN разности между ординатами прямой и ветви гиперболы:

MN = b x −b x2 −а2					= b		(x − x2		−a2 ) =
			a	a		a
=	b		(x − x2	−a2 )(x +		x2 −a2 )		=		ab	.
	a		x + x2 −a2							x2 −a2
								x +

Как видно, по мере возрастания х знаменатель дроби увеличивается; числитель — есть постоянная величина. Из чего заключаем, что длина отрезка MN стремится к нулю. Так как MN больше расстояния d от точки М до прямой, то

d и подавно стремится к нулю. Итак, прямые y =±ab x являются асимптотами

гиперболы (7.34).

Например, найдем уравнение асимптот гиперболы 2x 2 − 3y 2 = 6 .

У гиперболы (7.34) две асимптоты, определяемые уравнениями (7.35). Для начала найдем a и b заданной гиперболы.

Приведем уравнение гиперболы к каноническому виду, разделив при этом обе его части на 6. Получим

	x2		−	y2	=1.
3				2		a 2 = 3 a =		3, b2 = 2 b =
Таким образом,									2 . Подставляя найденные
эти значения a, b в уравнения асимптот (7.35), получаем
	y =			2 x, y =−		2 x или	2x −	3y = 0, 2x +	3y = 0 .
				3		3

При построении гиперболы (7.34) целесообразно сначала построить основной прямоугольник гиперболы (рисунок 62), провести прямые, проходящие через противоположные вершины этого прямоугольника, — асимптоты

гиперболы и отметить вершины А1, А2 гиперболы.

178

Рисунок 62

Уравнение равносторонней гиперболы, асимптотами которой служат оси координат.

Гипербола (7.34) называется равносторонней, если ее полуоси равны (а= b). Ее каноническое уравнение имеет вид

х2 − у2 =а2 .	(7.36)

Рисунок 63

Асимптоты равносторонней гиперболы имеют уравнения у = х и у=-х и, следовательно, являются биссектрисами координатных углов.

Рассмотрим уравнение этой гиперболы в новой системе координат Ох'у'

(рисунок 63), полученной из старой поворотом осей координат на угол				α =−	π .
Используем формулы поворота осей координат:					4
	′	′	sinα,
x = x cosα − y				(7.37)
	′	′	cosα.
y = x sinα + y

Подставляем значения х и у в уравнение (7.36):

179

′

−

π

′

−

π

2

′

−

π

′

−

π 2

2

,

x cos

4

− y

sin

4

− x sin

4

+ y cos

=a

4

1

′

′

2

1

′

′

2

2

′

′

a2

′

k

−

=a

y

=

,

=

,

′

2

(x

+ y )

2

(−x

+ y )

, x

2

y

x

где k = a2 . 2

Уравнение равносторонней гиперболы, для которой оси Ох и Qy являются асимптотами, будет иметь вид y = kx .

Рисунок 64

Дополнительные сведения о гиперболе

Эксцентриситетом гиперболы (7.34) называется отношение расстояния между фокусами к величине ее действительной оси:

ε =	с	.	(7.38)
	а		с>a, то эксцентриситет гиперболы больше
Так как для гиперболы

единицы: ε >1. Эксцентриситет характеризует форму гиперболы. Действительно, из равенства b2 =c2 −a2 следует,

	b2	=	c2	−1, т.е.	b		ε2 −1 и ε =	b	2
						=		1+ .
	а2		а2		а
								a

Таким образом, на основании последнего равенства мы можем утверждать, что чем меньше эксцентриситет гиперболы, тем меньше отношение ее полуосей, а значит, тем более вытянут ее основной прямоугольник.

Очевидно, эксцентриситет равносторонней гиперболы равен 2 . Действительно,

ε =	с	=	а2	+а2	=	2а2	=	2.
	а			2		а2
Фокальные радиусы r =								(x +c)2 + y2 и r = (x −c)2	+ y2	для точек правой
						1		2

180

	ветви гиперболы			имеют вид			r1 =εx +a, r2 =εx −a, a для	левой	—
	r1 =−(εx +a), r2 =−(εx −a) .
	Прямые	x =±		a		называются	директрисами гиперболы.	Так как	для
				ε
	гиперболы ε >1,	то	a			<a, откуда следует, что правая директриса расположена
			ε

между центром и правой вершиной гиперболы, левая— между центром и левой вершиной.

	Кривая, определяемая уравнением	у2	−	х2	=1, также есть гипербола,
		b2		a2

действительная ось 2b которой расположена на оси Оу, а мнимая ось 2а — на оси Ох. На рисунке 65 она изображена пунктиром.

		Рисунок 65
	Очевидно, что гиперболы	x2	−	y2	=1	и	у2	−	х2	=1	имеют общие
		a2		b2			b2		a2

асимптоты. Такие гиперболы называются сопряженными.

4 Парабола

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через р (р > 0).

Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к фокусу, а начало координат О расположим посередине между фокусом и директрисой (рисунок 66).

181

Рисунок 66

В выбранной системе фокус F имеет координаты (p / 2,0), а у равнение директрисы имеет x + 2p =0.

Пусть М(х,у) — произвольная точка параболы. Соединим точку М с F. Проведем отрезок MN перпендикулярно директрисе. Согласно определению параболы MF = MN . По формуле расстояния между двумя точками находим:

			p 2		, а		MN =			p 2
MF = x −			+ y2						x +	+( y − y )2 .
			2							2
Следовательно,
	p 2				+	p 2
x −	+ y2 =			x		2	.
	2
Возведя обе части уравнения в квадрат, получаем
x2 − px+		p2	+ y2	= x2 + px+				p2	,
т.е.	4						4
y2 =2px										(7.39)

Уравнение (7.39) называется каноническим уравнением параболы.

Например, определим параметр параболы y2 =2px, проходящей через точку А(2,4) .

Для этого подставим в уравнение параболы вместо текущих координат координаты точки А(2,4) и получим

42 =2p2 16=4p p =4,

Т.е. искомый параметр равен четырем.

Исследование формы параболы по ее уравнению

1 В уравнении (7.39) переменная у входит в четной степени, значит, парабола симметрична относительно оси Ox; ocь Ох является осью симметрии

182

параболы.

2 Так как р>0, то из (7.39) следует, что x ≥0. Следовательно, парабола расположена справа от оси Оу.

3 При х=0 имеем у=0. Следовательно, парабола проходит через начало координат.

4 При неограниченном возрастании х модуль у также неограниченно

возрастает. Таким образом парабола	y2 =2px имеет вид, изображенный на
рисунке 67. Точка О(0, 0) называется	вершиной параболы, отрезок FM =r

называется фокальным радиусом точки М.

Рисунок 67

Уравнения y2 =−2px, х2 =2pу, х2 =−2pу определяют параболы, изображенные на рисунке 68.

Рисунок 68

Нетрудно показать, что график квадратного трехчлена y = Аx2 + Вх+С, где А≠0, В,С любые действительные числа, представляет собой параболу в смысле, приведенного выше, ее определения.

183

5 Общее уравнение линий второго порядка

Уравнения кривых второго порядка с осями симметрии, параллельными координатным осям

Напишем сначала уравнение эллипса с центром в точке О1(х0 , у0 ), оси симметрии которого параллельны координатным осям Ох и Оу, и полуоси соответственно равны а и b. Поместим в центре эллипса О1 начало новой системы координат О1х′у′', оси которой О1х′ и О1 у′ параллельны соответствующим осям Ох и Оу, и одинаково с ними направлены (рисунок 69)

Рисунок 69

В этой системе координат уравнение эллипса имеет вид x′2 + y′2 =1 a2 b2

Так как х′=х−х0 , у′= у− у0 , то в старой системе координат уравнение эллипса запишется в виде

(x − х0 )2 +( y − у0 )2 =1 a2 b2

- уравнение параболы с центром в точке О1(х0 , у0 ) и полуосями а и b.

Аналогично рассуждая, получим уравнение гиперболы с центром в точке О1(х0 , у0 ), действительной полуосью а и мнимой полуосью b (рисунок 70):

(x − х0 )2 −( y − у0 )2 =1. a2 b2

Рисунок 70

184

И, наконец, параболы, изображенные на рисунке 71, имеют соответствующие уравнения.

Рисунок 71

Уравнение Ax2 +Cy2 +Dx+Ey+F =0 и его геометрическое толкование

Очевидно, уравнения эллипса, гиперболы, параболы и уравнение окружности после преобразований (раскрыть скобки, перенести все члены уравнения в одну сторону, привести подобные члены, ввести новые обозначения для коэффициентов) можно записать с помощью единого уравнения вида

Ax2 +Cy2 +Dx+Ey+F =0,

(7.40)

где коэффициенты А и С не равны нулю одновременно.

Уравнение (7.40) является частным случаем общего уравнения второй степени относительно x и y , т.е. уравнения вида

Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 ,

(7.41)

которое называют общим уравнением кривой второго порядка на плоскости.

Рассмотрим общее уравнение кривой второго порядка, т.е. уравнение

(7.41), где A + B + C ≠ 0 , B :

Ax2 + Cy2 + Dx + Ey + F = 0 .

(7.42)

Выясним, какие кривые соответствуют этому уравнению. Возможны следующие случаи:

1 AC > 0 (эллиптический тип). Без ограничения общности можно считать, что A и C - положительные числа.

В уравнении (7.42) дополняем до полного квадрата члены, содержащие x2

185

и x , а также y2 и y . После этого уравнение можно будет записать в виде

A(x − x	0	)2	+ C(y − y	0	)2	= F .	(7.43)
						1
Если F1 > 0 , то уравнение (7.43) приводится к виду
(x − x0 )2 +			(y − y0 )2	=1		,
a2			b2

где a2 = F1 A ; b2 = F1 C . Это уравнение определяет эллипс.

Если F1 < 0 , то уравнению (7.43) никакие действительные значения x и y

не удовлетворяют, следовательно, этому уравнению соответствует пустое множество.

Если F1 = 0 , то уравнение (7.43) принимает вид

A(x − x0 )2 + C(y − y0 )2 = 0

и определяет точку M (x0 , y0 ).

2 AC < 0 (гиперболический тип). Не нарушая общности, можно считать, что A > 0 , C < 0 . Как и в первом случае, уравнение (7.42) можно привести к виду

(7.43).

Если F1 > 0 , то уравнение (7.43) можно записать в виде

(x − x0 )2	−	(y − y0 )2	=1.
a2		b2

Оно определяет гиперболу, действительная ось которой параллельна оси Ox . Если F1 < 0 , то получим гиперболу, заданную уравнением

(y − y0 )2	−	(x − x0 )2	=1.
b2		a2

Действительная ось этой гиперболы параллельна оси Oy . Если F1 = 0 , то уравнение (7.43) принимает вид

A(x − x0 )2 + C(y − y0 )2 = 0 .

Докажем, что ему соответствует пара пересекающихся прямых.

Введем обозначения A = m2 , C = −n2 и запишем уравнение в виде

m2 (x − x0 )2 − n2 (y − y0 )2 = 0

или (m(x − x0 )− n(y − y0 ))(m(x − x0 )+ n(y − y0 ))= 0 .

Это уравнение равносильно следующим двум: m(x − x0 )− n(y − y0 )= 0 ;

m(x − x0 )+ n(y − y0 )= 0 ,

каждое из которых определяет прямую, проходящую через точку M (x0 , y0 ).

3 AC = 0 (параболический тип). Предположим, что A ≠ 0 , C = 0 , т.е.

уравнение (7.42) имеет вид

Ax2 + Dx + Ey + F = 0 .

Не нарушая общности, можно считать, что A > 0 . Дополнив члены, содержащие

186

x2 и x , до полного квадрата, получим A(x − x0 )2 + Ey = F1 . Если E ≠ 0 , то уравнение можно записать в виде

(y − y0 )= a(x − x0 )2 .

Этому уравнению соответствует парабола с осью симметрии, параллельной оси

Oy .

Если E = 0 и F1 > 0 , то уравнение

A(x − x	0	)2 = F	(7.44)
		1
равносильно уравнениями
A(x − x0 )+ F1 = 0 ;			A(x − x0 )− F1 = 0 ,

которые определяют пару параллельных прямых.

Если E = 0 и F1 < 0 , то получим также уравнение (7.44), которому в этом

случае соответствует пустое множество.

Если E = 0 и F1 = 0 , то уравнение примет вид

A(x − x0 )2 = 0 .

Оно определяет пару совпадающих прямых x − x0 = 0 .

Если предположить, что A = C , C ≠ 0 , то уравнение (7.42) будет иметь вид

Cy2 + Dx + Ey + F = 0 .

Аналогично предыдущему можно доказать, что это уравнение при D ≠ 0 определяет параболу с осью симметрии, параллельной оси Ox , и может быть приведено к виду (x − x0 )= a(y − y0 )2 .

Если D = 0 , то уравнение определяет пару параллельных (в частности слившихся) прямых или пустое множество.

Итак, справедлива следующая теорема:

Теорема 7.2. Уравнение (7.40) всегда определяет: либо окружность (при

А=С), либо эллипс (при А С>0), либо гиперболу (при А С<0), либо параболу (при

АС=0). При этом возможны случаи вырождения: для эллипса (окружности) —

вточку или мнимый эллипс (окружность), для гиперболы — в пару пересекающихся прямых, для параболы — в пару параллельных прямых.

Например, установим вид кривой второго порядка, заданной уравнением

4x2 − y2 +8x −8y −12 =0(АС=−4 <0).

Для этого преобразуем исходное уравнение, выделив полный квадрат (и по x и по y ):

4(x2 +2x +1) −(y2 +8y +16) −4 +16−12=0, 4(x +1)2 −(y +4)2 =0,

(2(x +1) +(y +4)) (2(x +1) −(y +4)) =0, (2x + y +6)(2x − y −2) =0.

Это уравнение определяет две пересекающиеся прямые 2x + y +6 =0 и 2x − y −6 =0.

187

Общее уравнение второго порядка

Рассмотрим теперь общее уравнение второй степени с двумя неизвестными (запишем его в более удобной форме):

Ax2 +2Bxy+Cy2 +2Dx+2Ey+ F =0.

(7.45)

Оно отличается от уравнения (7.42) присутствием члена с произведением координат (В≠0) . Докажем, что можно, путем поворота координатных осей на

угол α, преобразовать это уравнение, таким образом, чтобы в нем член с произведением координат отсутствовал.

Действительно, используя формулы поворота осей

x = x′cosα − y′sinα,y = x′sinα + y′cosα.

Выразим старые координаты через новые:

′

′

2

+

′

′

′

′

′

′

2

A(x cosα − y sinα)

2B(x cosα − y sinα)(x sinα + y cosα) +C(x sinα + y cosα)

′

′

′

′

+F =0.

+2D(x cosα − y sinα) +2Е(x sinα

+ y cosα)

Выберем угол

α

так, чтобы коэффициент при

′

y

′

обратился в нуль, т.е. чтобы

x

выполнялось равенство

−2Acosαsinα +2B(cos2 α −sin2 α) +2Csinαcosα =0,

т.е.

(C − A)sin2α +2Bcos2α =0,

(7.46)

т.е. 2Bcos2α =(A−C)sin2α..

Отсюда

2B

tg2α =

.

(7.47)

A−C

Таким образом, при повороте осей на угол α, удовлетворяющий условию

(7.47), уравнение (7.46) сводится к уравнению

Ax2 + Cy2 + 2Dx + 2Ey + F = 0 .

(7.48)

Вывод: общее уравнение второго порядка (7.45) определяет на плоскости следующие кривые: окружность, гиперболу, эллипс, параболу.

7.7 Вопросы для самоконтроля

1	Сформулируйте определение аффинной системы координат на
плоскости.
2	Сформулируйте определение координат точки	относительно
аффинного репера.
3	Как найти координаты вектора по координатам точек его начала и
конца?

4Запишите формулы для нахождения координат точки, делящей отрезок

вотношении λ.

5Сформулируйте определение прямоугольной декартовой системы координат на плоскости.

188

6Запишите формулу для нахождения расстояния между точками.

7Какая система координат называется полярной?

8Запишите формулы для нахождения полярных координат точки через прямоугольные декартовые координаты и наоборот.

9Что понимают под параллельным переносом осей координат?

10Что понимают под поворотом осей координат?

11Запишите уравнение линии на плоскости.

12Запишите уравнение прямой с угловым коэффициентом.

13Запишите уравнение прямой, проходящей через две точки.

14	Запишите	формулы для нахождения угла между	прямыми
L1 : y = k1 x + b1 и L2 : y = k2 x + b2 .
15	Запишите	условия параллельности и перпендикулярности	прямых
L1 : y = k1 x + b1 и L2 : y = k2 x + b2 .

16Какой вид имеет общее уравнение прямой на плоскости?

17Какую прямую определяет уравнение вида Ах + Ву = 0 ?

18Запишите уравнение прямой «в отрезках».

19По какой формуле можно найти расстояние от точки до плоскости?

20Запишите уравнение окружности.

21Сформулируйте определение эллипса.

22Запишите каноническое уравнение эллипса.

23Что называется эксцентриситетом эллипса?

24Дайте определение гиперболы.

25Запишите каноническое уравнение гиперболы.

26Какая гипербола называется равносторонней?

27Запишите формулы для нахождения эксцентриситета и асимптот гиперболы.

28Сформулируйте определение параболы.

29	Изобразите	параболы,	заданные уравнениями		у2 = 2 рх, x2 = 2 py ,
( p > 0 ).	Запишите уравнения эллипса с центром в точке O1(x0 ; y0 ) и полуосями
30
a , b, параллельные осям координат.
31	Запишите уравнения гиперболы с центром в точке O1(x0 ; y0 ),
действительной осью - a , мнимой осью - b.
32	Уравнение	Ax2 + Cy2 + Dx + Ey + F = 0		и	его	геометрическое
толкование в случае AC > 0 .
33	Уравнение	Ax2 + Cy2 + Dx + Ey + F = 0		и	его	геометрическое
толкование в случае AC < 0 .
34	Уравнение	Ax2 + Cy2 + Dx + Ey + F = 0		и	его	геометрическое
толкование в случае AC = 0 .
35	Общее	уравнение	кривой	второго		порядка

Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 и его геометрическое толкование.

189