Глава 6 Векторная алгебра

6.1 Векторы. Основные понятия. Линейные операции над векторами

Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура.

Другие величины, например, сила, скорость, ускорение определяются не только своим числовым значением, но и направлением. Например, при движении тела следует указать не только скорость, с которой движется тело, но и направление движения. Точно так же, изучая действие какой-либо силы, необходимо указать не только значение этой силы, но и направление ее действия. Такие величины называются векторными.

Вектор это направленный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Если А - начало вектора, а В - его конец, то

вектор обозначается символом АВ или а.

Вектор ВА (у него начало в точке В, а конец в точке А) называется противоположным вектору АВ. Вектор противоположный вектору а, обозначается −а.

Длиной или модулем вектора АВ называется длина отрезка АВи обозначается АВ .

Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 0 . Нулевой вектор направления не имеет.

Вектор, длина которого равна единице, называется единичным вектором и обозначается е . Единичный вектор, направление которого совпадает с

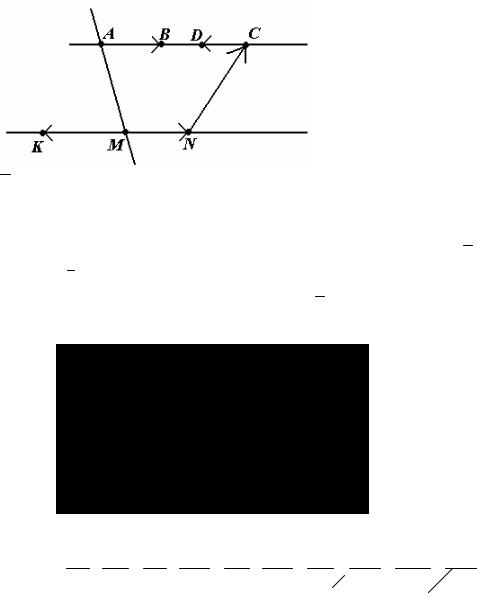
направлением вектора а, называется ортом вектора а и обозначается a0 . Векторы а и b называются коллинеарными, если они лежат на одной

прямой или на параллельных прямых: обозначают аb .

Рисунок 17

На рисунке 17 AB|| CD , AB || MN , CD || MN , AB || NC , MN || NC .

Среди коллинеарных векторов выделяют сонаправленные и противоположнонаправленные.

132

Коллинеарные векторы называются сонаправленными, если относительно прямой, соединяющих их начала оба вектора окажутся в одной полуплоскости. В противном случае векторы называются противоположнонаправленными.

Например, векторы AB и MN - сонаправлены, так как относительно прямой (AM ) они расположены в одной полуплоскости; а векторы AB и MK относительно этой же прямой (AM ) расположены в разных полуплоскостях.

Следовательно, AB и MK - противоположнонаправлены. Знак ↑↑ используется для сонаправленных векторов; для противоположнонаправленных используется знак ↓↑.

На рисунке 17 AB ↑↑ MN , AB ↑↓ CD , AB ↑↓ MK .

Принято нуль – вектор считать коллинеарным с любым другим.

Два вектора а и b называются равными ( а=b ), если они коллинеарны,

одинаково направлены и имеют одинаковые длины.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку пространства.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

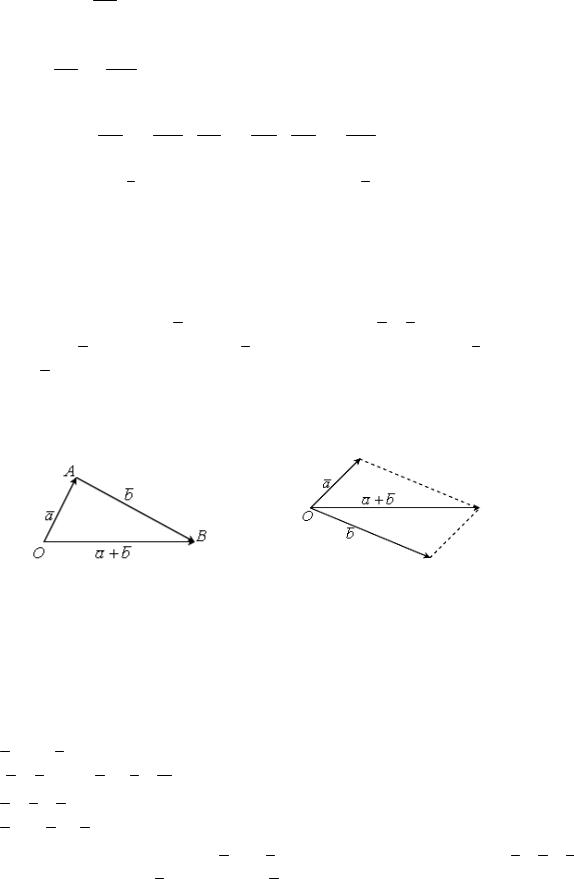
Суммой двух векторов a и b называется вектор a + b , который направлен

из начала вектора a в конец вектора b при условии, что вектор b отложен из

конца вектора a .

Для геометрического представления суммы векторов используют правила «треугольника» и «параллелограмма», проиллюстрированные на рисунках 18 и 19 соответственно.

Рисунок 18

Рисунок 19

Аналогично определяется сумма трех и более векторов. Суммой конечного числа векторов будет вектор, направленный из начала первого в конец последнего вектора, при условии, что каждый последующий вектор отложен из конца предыдущего (правило «многоугольника»).

Свойства операции сложения векторов

1)a + b = b + a (коммутативность),

2)(a + b) + c = a + (b + c) (ассоциативность),

3)a + o = a ,

4)a + (−a) = o .

Разностью двух векторов a и b называется такой вектор x = a − b , который в сумме с вектором b дает вектор a , т.е.

133

a − b = x , если b + x = a .

Чтобы построить разность a − b двух векторов a и b, нужно отложить их из одной точки и вектор разности будет направлен из конца второго вектора (вычитаемого) в конец первого вектора (уменьшаемого) (рисунок 20).

Рисунок 20				Рисунок 21
Отметим, что поскольку a −		= a + (−		), то разность a −		равна сумме
	b		b		b

двух векторов a и (−b ), где (−b )- вектор, противоположный вектору b (рисунок

21).

Произведением вектора a ≠ 0 на число α ≠ 0 называется вектор b =αa ,

удовлетворяющий условиям:

1)b = α a ,

2)b ↑↑ a , если α > 0 ; b ↑↓ a , если α < 0 . Очевидно, что b = 0 , если α = 0 или a = 0 .

Из определения следует, что в результате умножения вектора на

действительное число получается вектор, коллинеарный данному, то есть αa ║a .

Свойства умножения вектора на число

1.α(βa )= (αβ )a (α, β R ),

2.1 a = a,

3.(α + β)a =αa + βa (α, β R ),

4.α(a +b )=αa +αb (α R ).

Теорема 6.1 Для любых двух коллинеарных векторов

a

и

, где

a ≠

,

b

0

существует единственное число α такое, что

=αa .

b

Доказательство.

Пусть векторы

a и

коллинеарны.

Возможны

два

b

случая:

а) Векторы a и

сонаправлены ( а ↑↑

). Рассмотрим число α =

b

и

b

b

a

сравним два вектора

и αa . Имеем

αa

=

α

a

=

b

a

=

,

т.е. длины векторов

b

b

a

одинаковы. Сравним

направления:

а ↑↑αa (α > 0) .

По

условию

а ↑↑

,

b

следовательно, αа ↑↑

.

Так как длины и направления векторов одинаковы, то

b

=αa .

b

б) Векторы a

и

противоположно направлены ( а ↑↓

). Рассмотрим

b

b

134

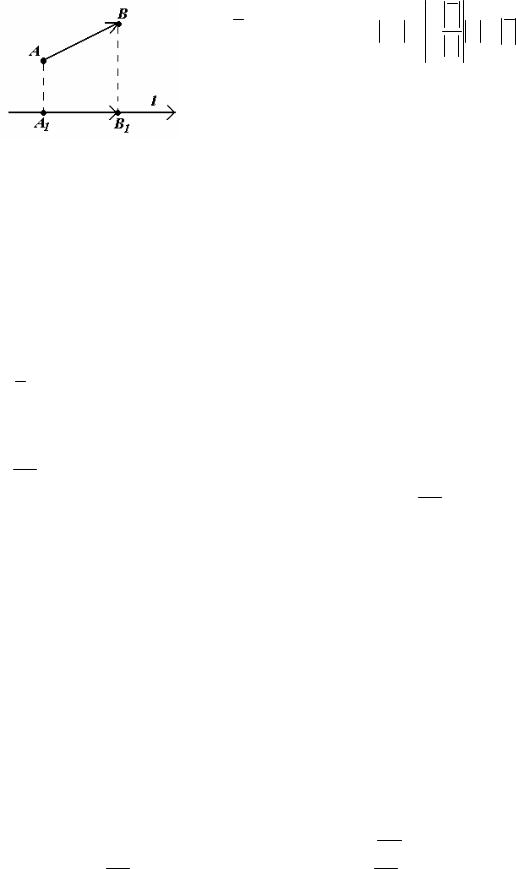
b b

число α = − a и сравним два вектора b и αa . Имеем αa = − a a = b , т.е.

длины векторов одинаковы. Сравним направления: а ↑↓αa (α < 0) . По условию

а ↑↓

, следовательно, αа ↑↓

. Так

как

длины и

направления векторов

b

b

одинаковы, то и в этом случае

=αa .

b

векторы a и

Пусть

теперь

=αa , тогда по

определению

либо

b

b

сонаправлены, либо противоположно направлены, т.е. всегда коллинеарны.

Докажем единственность

существования числа

α для коллинеарных

векторов a и

. Предположим,

что существуют два числа α и α1 такие, что

b

=αa

и

=α1a . Тогда из условия αa =α1а

следует,

что числа α и α1 одного

b

b

знака,

а из условия

αa

=

α1а

, что

α

=

α1

.

Значит,

α =α1 , что противоречит

предложению. Число α единственное.

Из теоремы следует, что

=αa

- необходимое и

достаточное условие коллинеарности двух

b

векторов a и b .

6.2 Проекция вектора на ось

Пусть AB - произвольный ненулевой вектор. Обозначим через A1 и B1 проекции на ось l соответственно начала A и конца B вектора AB и рассмотрим

вектор

A1B1

.

Проекцией вектора

на ось l называется положительное число

,

AB

A1B1

если вектор

и ось l одинаково направлены и отрицательное число −

,

A1B1

A1B1

если вектор

и ось l противоположно направлены (рисунок 22)

A1B1

Рисунок 22

Если точки A1 и B1 совпадают, то проекция вектора AB на ось l равна 0. Проекция вектора AB на ось l обозначается так: прl AB .

Угол ϕ между вектором a и осью l изображен на рисунке 23. Очевидно,

0 ≤ϕ ≤π .

135

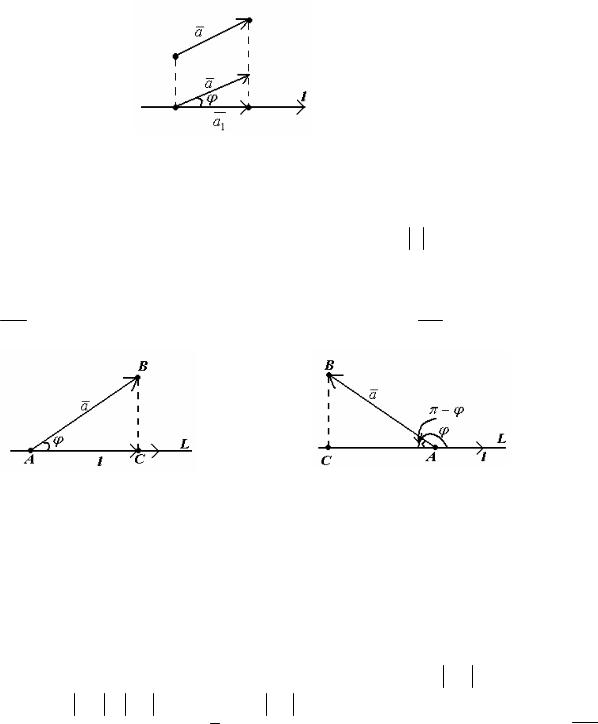
Рисунок 23

Свойства проекций

1. Проекция вектора a на осью l равна произведению модуля вектора a на косинус угла ϕ между вектором и осью, т.е. прl a = a cosϕ .

Действительно, пусть l лежит на прямой L, а его началом является точка А. Совместим начало вектора а с точкой А, и пусть его концом будет точка В (рисунок 24). Построим ортогональную проекцию С точки В на прямую L. Тогда

вектор АС является ортогональной проекцией вектора а = АВ на прямую L.

а)

б)

Рисунок 24

Если угол ϕ между векторами а

острый (см. рисунок 24,

а), то из

и l

прямоугольного треугольника ACB имеем

АС

=

АВ

cosϕ .

и точка С лежат

Если угол ϕ тупой (см. рисунок 24,б), то конец вектора l

по разные стороны от точки А. Это

значит, что векторы

и

имеют

АС

l

противоположные направления, а проекция вектора аравна − АС . Поэтому АС = АВсos(π −ϕ) = − АВ cosϕ .

Если угол ϕ = 900 или а = 0 , то точка С совпадает с точкой А и вектор AC

является нулевым вектором. Однако сos900 = 0 , следовательно, и в этом случае данное свойство справедливо.

2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось, т.е.

прl (a1 + а2 ) = прl a1 + прl a2 .

Действительно, пусть точки A и A1 - соответственно начало и конец вектора a1 , точки A1 и A2 - начало и конец вектора a2 (рисунок 25).

136

		Рисунок 25
Обозначим через A′, A1′, A2′		соответственно проекции точек A, A1 , A2 на ось
l . По определению, прl a1 = A′A1′,		прl a2 = A1′A2′ , прl (a1 + a2 ) = прl			= A′A2′ .
				AA2
Тогда	справедливо	следующее	А′А2′ = А′А1′ + А1′А2′ .			Отсюда

прl (a1 + а2 ) = прl a1 + прl a2 .

3. При умножении вектора a на число λ его проекция на ось также умножается на это число, т.е. прl (λ a ) = λ прl a .

Доказательство этого свойства предлагаем читателю выполнить самостоятельно.

6.3 Линейная зависимость и линейная независимость векторов. Свойства линейно зависимой системы векторов

Пусть даны векторы a1, a2 ,..., an и действительные числа α1,α2 ,...,αn . Рассмотрим вектор a = α1a1 +α2a2 +... +αnan , который назовем линейной комбинацией векторов a1, a2 ,..., an ; действительные числа α1,α2 ,...,αn назовем

коэффициентами линейной комбинации.

Очевидно, что, выбирая другую совокупность чисел β1, β2 ,..., βn , получим другую линейную комбинацию тех же самых векторов: b = β1a1 + β2a2 +... + βnan .

То есть можно построить бесчисленное множество линейных комбинаций одной и той же системы векторов.

Система векторов a1, a2 ,..., an называется линейно зависимой, если существуют действительные числа α1,α2 ,...,αn , из которых хотя бы одно отлично от нуля, такие, что линейная комбинация векторов a1, a2 ,..., an с этими числами равна нулевому вектору, то есть:

α1a1 +α2a2 +... +αnan =						(6.1)
		0
Если	соотношение	(6.1)		выполняется	только	при условии

α1 = α2 = ... = αn = 0 , то система векторов называется линейно независимой.

Свойства линейно зависимой системы векторов

1. Если один из векторов системы нуль-вектор, то вся система векторов линейно зависима.

Действительно, пусть в системе a1 , a2 ,..., an−1 ,0 таким вектором является

137

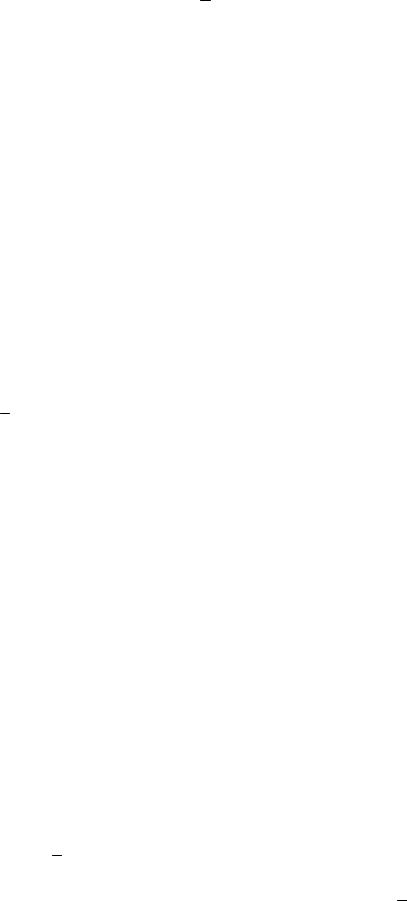
последний вектор (этого всегда можно добиться путем перенумерации векторов). Рассмотрим систему чисел 0,0,0,…,1.

Очевидно, что 0 a1 + 0 a2 + ... + 0 an−1 +1 0 = 0 , поэтому система векторов линейно зависима.

2. Если один из векторов системы является линейной комбинацией остальных векторов, то вся система векторов линейно зависима (справедливо и обратное утверждение).

Доказательство. Необходимость. Предположим, что векторы a1, a2 ,..., an линейно зависимы. Согласно определению линейной зависимости векторов, в равенстве α1a1 +α2a2 +... +αnan = 0 слева есть хотя бы один ненулевой коэффициент, например α1. Оставив первое слагаемое в левой части равенства,

перенесем остальные слагаемые в правую часть, при этом меняем у них знаки. Разделив полученное равенство на α1, получим

а	= −	α2	a		−... −	αn	a	n	,
		α1
1				2		α1
т.е. представили вектор а1 в виде линейной комбинации векторов a2 ,..., an .

Достаточность. Пусть, например, первый вектор а1 можно представить в

виде линейной комбинации остальных векторов: a1 = β2 a2 + ... + βn an .

Перенесем все слагаемые из правой части в левую, тогда получим

a1 − β2 a2 − ... − βn an = 0 ,

т.е. линейную комбинацию векторов a1, a2 ,..., an с коэффициентами a1 =1,α2 = −β2 ,...αn = −βn , равную нулевому вектору. В этой комбинации не все

коэффициенты равны нулю. Согласно определению линейной зависимости векторов, векторы a1, a2 ,..., an линейно зависимы. Что и требовалось доказать.

3. Если часть системы векторов линейно зависима, то вся система

векторов линейно зависима.	например, α1a1 + α2a2 + ...+ αsas =				и α1 ≠ 0 , то
Действительно, если,				0
будет выполнено равенство
α1a1 +α2a2 +... +αs as	+ 0as +1 + 0as +2 +... + 0an =		,
		0
причем α1 ≠ 0 .

4.Система векторов, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.

Предлагаем свойства 4 читателю доказать самостоятельно.

5.Система векторов, состоящая из двух векторов, линейно зависима тогда и только тогда, когда эти векторы коллинеарны.

Действительно, если векторы а и b линейно зависимы, то один из них, например, а, выражается через другой, т.е. а = λb , где λ -действительное число.

Согласно определению произведения вектора на число, векторы а и b являются коллинеарными.

Пусть теперь векторы а и b коллинеарны. Если они оба нулевые, то очевидно, что они линейно зависимы, так как любая их линейная комбинация

равна нулевому вектору. Предположим, что один из этих векторов не равен 0 ,

138

например b . Обозначим через λ отношение длин векторов: λ = bа .

Коллинеарные векторы могут быть сонаправленными или противоположно направленными. Тогда проверяя определение произведения вектора на число,

убеждаемся, что а = λb . Согласно свойству 2, векторы а и b линейно зависимы,

что и требовалось доказать.

Замечание. Любые два неколлинеарных между собой вектора образуют линейно независимую систему векторов.

6.Система векторов, состоящая из трех векторов, линейно зависима тогда и только тогда, когда они компланарны.

7.Любые четыре вектора в трехмерном пространстве всегда линейно зависимы.

Вывод: Система векторов, содержащая более чем три вектора в трехмерном пространстве, всегда линейно зависима.

6.4 Базис системы векторов. Координаты вектора относительно базиса

Пусть задана некоторая система векторов S . Число векторов в системе может быть конечным или бесконечным.

Подсистема S′ системы S называется максимально линейно независимой подсистемой, если она удовлетворяет двум условиям:

1S′ - линейно независима;

2При добавлении к системе S′ любого вектора системы S она становится линейно зависимой.

Базисом системы векторов S называется любая максимально линейно независимая подсистема системы S .

Базисом на плоскости назовем два неколлинеарных вектора этой плоскости, взятых в определенном порядке. Обозначение: {e1, e2}.

Базисом в пространстве назовем три некомпланарных вектора, взятых в определенном порядке. Обозначение {e1, e2 , e3}.

В трехмерном пространстве существует бесконечное множество базисов. Рассмотрим в трехмерном пространстве некоторый базис {e1, e2 , e3} и

любой вектор a . Если вектор a	представлен	в виде	линейной		комбинации
векторов e1, e2 , e3 , то есть a = xe1 + ye2 + ze3 , то говорят,			что вектор a разложен
по векторам базиса, а действительные числа x, y,		z называются коэффициентами
разложения.
Координатами вектора a в базисе {e1, e2 , e3} называются коэффициенты
разложения вектора по векторам базиса. Обозначение: a{x, y, z}{e , e				2	, e }.
			1		3
Теорема 6.2 Координаты вектора в фиксированном базисе находятся
единственным образом.		a кроме координат x, y, z в
Доказательство. Допустим,	что у вектора

139

базисе {e1, e2 , e3} имеются другие координаты x′, y′, z′. Тогда a = xe1 + ye2 + ze3 = x′e1 + y′e2 + z′e3 .

Следовательно,

(x − x′)e1 + ( y − y′)e2 + (z − z′)e3 = 0 .

По условию векторы базиса {e1, e2 , e3} линейно независимы, а значит, x − x′ = 0, y − y′ = 0, z − z′ = 0 . Поэтому x = x′ , y = y′, z = z′. Других координат у вектора нет.

Свойства координат векторов

1. Координаты суммы (разности) двух векторов, заданных своими

координатами в некотором базисе, равны сумме (разности) соответствующих

координат

этих векторов,

то есть

если

a{a1, a2

, a3

}{e , e

, e }

и

{b1, b2 , b3}{e , e

, e }, то

1

2

3

b

1

2

3

a ±

={a1 ± b1, a2 ± b2 , a3 ± b3}{e1 , e2 , e3 }.

b

Действительно, рассмотрим векторное пространство V3 . Фиксируем в V3

базис {e1, e2 , e3}.

Возьмем два

произвольных

вектора

а и

и

запишем

их

b

разложения в выбранном базисе:

a = a1e1 + a2 e2 + a3e3 , b = b1e1 + b2 e2 + b3e3 .

Используя свойства линейных операций, вычисляем сумму (разность) этих векторов:

a + b = (a1e1 + a2 e2 + a3e3 ) + (b1e1 + b2 e2 + b3e3 ) = = (a1 + b1 )e1 + (a2 + b2 )e2 + (a3 + b3 )e3 .

Получили разложение суммы (разности) векторов в фиксированном базисе. Отсюда заключаем, что координаты аi и bi исходных слагаемых,

соответствующие одному вектору ei в базисе {e1, e2 , e3}, складываются

(вычитаются).

2. Координаты произведения вектора на действительное число равны произведению этого числа на соответствующие координаты вектора в

некотором базисе, а именно, если a{a1, a2 , a3}{e1 , e2 , e3 }, то

b =αa ={αa1, αa2 , αa3}{e1 , e2 , e3 }.

3. Пусть даны векторы a{a1, a2 , a3}{e1 , e2 , e3 } и b{b1, b2 , b3}{e1 , e2 , e3 } и пусть вектор с =αa + βb , тогда на основе предыдущих свойств нетрудно показать,

что вектор с имеет следующие координаты с(αa1 + βb1 ,αa2 + βb2 ,αa3 + βb3 ) .

4. Условие коллинеарности двух векторов, заданных своими координатами в некотором базисе:

Пусть относительно базиса {e1, e2 , e3} даны векторы a{a1, a2 , a3}, b{b1, b2 , b3} и a ||b , тогда по необходимому и достаточному условию b =αa или

140

в координатной форме:
b	=αa			a			a			a
1	1							2
b	=αa	2	или		1	=			=	3	- условие коллинеарности двух векторов в
2				b1			b2			b3
	=αa3
b3

координатной форме.

6.5 Ортонормированный базис. Направляющие косинусы вектора. Длина вектора

Рассмотрим в пространстве два неколлинеарнных вектора a, b и отложим их от произвольной точки O пространства (a = OA, b = OB)(рисунок 26).

Рисунок 26

Углом между векторами a и b , если особо не оговорено, будем называть угол AOB , величина которого не превышает π .

Принято угол между сонаправленными векторами считать равным нулю, то есть для любых a и b :

0 ≤ a; b ≤ π .

Два вектора a и b называются ортогональными, если угол между ними равен 90o , т.е. если a b , то a и b ортогональны.

Принято нулевой вектор считать ортогональным с любым другим вектором.

Базис {e1, e2 , e3} трехмерного пространства называется ортонормированным, если выполняются два условия:

1)все векторы этого базиса единичные;

2)векторы базиса попарно ортогональны, то есть e1 e2 , e2 e3, e1 e3 .

Ортонормированный базис в пространстве V3 принято обозначать, с учетом порядка, буквами, {i , j, k }, в V2 - соответственно {i , j} и в V1 -{i }.

Вектора i , j, k называют ортами.

Пусть дан произвольный вектор a = {x, y, z}; будем считать, что a

выходит из начала координат и не лежит ни в одной координатной плоскости. Проведем через точку А плоскости, перпендикулярные координатным осям. Вместе с координатными плоскостями они образуют прямоугольный параллелепипед, диагональю которого служит отрезок ОА (рисунок 27).

141

Рисунок 27

Из элементарной геометрии известно, что квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его измерений. Следовательно,

ОА

2 =

ОА

2 +

ОА

y

2 +

ОА

2 .

х

z

Но

ОА

=

a

,

ОАх

=

x

,

ОАy

=

y

,

ОАz

=

z

; таким образом, получаем

a

2 = x 2 + y 2 + z 2 ,

то есть

a = x2 + y 2 + z 2 .

(6.2)

Формула (6.2) выражает длину произвольного вектора через его

координаты.						углы между вектором a и осями координат. Из
Обозначим через α, β, γ
формул прl a =		a		cosϕ и a =		x2 + y 2 + z 2	получаем
cosα =				x	, cos β =		y	,
		x2 + y 2 + z 2
						x2 + y 2 + z 2
cosα =				z	;			(6.3)
		x2 + y 2 + z 2

cosα, cos β, cos γ называются направляющими косинусами вектора a .

Возводя в квадрат левую и правую части равенства (6.3) и суммируя полученные результаты, имеем

cos 2 α +cos 2 β + cos 2 γ =1,

т.е. сумма квадратов направляющих косинусов любого вектора равна единице.

Например, вычислим направляющие косинусы вектора а ={12,−15,−16}.

Решение. Найдем длину вектора а = 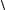122 + (−15)2 + (−16)2 = 25 . Далее, используя формулу (6.3) имеем

142

cosα = 1225 , cos β = −1525 , cosγ = −1625 .

6.6 Скалярное произведение векторов и его свойства

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначение: а b или (а,b). Итак, по определению

а		=		a				cosϕ,	(6.4)
	b						b

где ϕ=(а,b ).

Формуле (6.4) можно придать иной вид.

Рисунок 28
Так как a cosϕ=прba (рисунок 28), а b cosϕ=прab , то получаем:
ab =b прba = a прab ,	(6.5)

т.е. скалярное произведение двух векторов равно произведению модуля одного

из них, на проекцию другого на ось, сонаправленную с первым вектором.

Заметим, что

a b > 0 , если cos(a, b )> 0 , то есть 0 ≤ (a, b )<π 2 ; a b < 0 , если cos a , b < 0 , то есть π2 < a , b ≤ π;

a b = 0 , если либо a = 0 , либо b = 0 , либо cos(a, b )= 0 , то есть a b .

Таким образом, скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы ортогональны, то есть

еслиa ≠ 0, b ≠ 0 , но a b = 0 , то a b .

Свойства скалярного произведения векторов

1. a b = b a (коммутативность);

Действительно, свойство непосредственно вытекает из определения скалярного произведения векторов, так как

a b = a b cos ϕ = b a cos(− ϕ)= b a .

2. λa b = λ(a b ) (λ R);

143

Действительно, если b = 0 - нулевой вектор, то обе части доказываемого равенства равны нулю. Если же b ≠ 0 , то, используя выражение скалярного произведения через ортогональную проекцию вектора a на направление вектора b и свойства проекций получаем

(λа)b = b (λa ) = b прb (λa) = λ b прb a = λ(ab ) .

3. (a + b ) c = a c + b c (дистрибутивность относительно сложения

векторов).

Третье свойство предлагаем читателю доказать самостоятельно.

4. Скалярный квадрат вектора есть неотрицательное число, причем, скалярный квадрат вектора равен нулю тогда и только тогда, когда этот вектор нулевой, то есть

a a = a 2 ≥ 0 и a 2 = 0 a = 0.

Из свойства 4 следует, что

a 2 =

a

a

cos 0 =

a

2 a 2 =

a

2

или a = a 2 .

Таким образом, скалярный квадрат вектора равен квадрату его длины.

5.

Скалярное

произведение

векторов

a ={a1, a2 , a3}{i , j, k

}

и

b ={b1, b2 , b3}{i , j, k }, заданных в ортонормированном базисе, равно сумме

произведений одноименных координат этих векторов, т.е.
a b = a1b1 + a2b2 + a3b3 .	(6.6)

Действительно, так как векторы а и b заданы своими координатами в ортонормированном базисе, то это означает, что имеются разложения

a = a1i + a2 j + a3 k и b = b1i + b2 j + b3 k .

Используя разложения векторов а и b , а также свойства скалярного произведения имеем

ab = (a1i + a2 j + a3 k )(b1i + b2 j + b3 k ) = a1b1i i + a1b2i j + a1b3i k +

+ a2b1

ji + a2b2 jj + a2b3 jk + a3b1ki + a3b2 kj + a3b3 kk =

2 + a

b

2 + a

2

= a b + a

b

+ a

b .

= a b i

2

2

j

3

b k

2

2

3

1

1

3

1

1

3

Окончательный ответ получен с учетом того, что ортонормированность

базиса

{i

,

}

означает

выполнение

равенств

, k

j

i j = i

k = jk = 0 ,

=1.Таким образом

i

i = jj = kk

a b = a1b1 + a2b2 + a3b3 .

6. Укажем еще одну формулу, вытекающую из определения скалярного произведения и формул для нахождения длин векторов, координаты которых известны в ортонормированном базисе.

Пусть a ={a1, a2 , a3}{i , j, k } и b ={b1, b2 , b3}{i , j, k }. Так как a b = a b cosϕ , то

144

b

a1b1 + a2b2 + a3b3

cos ϕ =

a

или cosϕ =

(6.7)

a12 + a22 + a32 b12 + b22 + b32

b

a

Взаключении этого параграфа приведем пример применения определения

исвойств скалярного произведения при решении следующей задачи:

Найти (a, b ) , если a = m − 3n , b = 2m + 2n, m = 3, n = 3,(m,n) =π .

Решение.

(a, b ) = (m − 3n, 2m + 2n) = (m,2m + 2n) + (−3n,2m + 2n) = (m,2m) + (m,2n) + + (−3n,2m) + (−3n,2n) = 2(m, m) + 2(m, n) − 6(n, m) − 6(n, n) = 2 m 2 − 6 n 2 − − 4 mn cos(m, n) = 2 32 − 6 32 − 4 3 3 cosπ =18 − 54 + 36 = 0.

Итак, (a, b ) = 0 , то есть векторы a и b ортогональны.

6.7 Векторное произведение двух векторов и его свойства

Три некомпланарных вектора a, b , c взятых в указанном порядке, образуют правую тройку, если из конца третьего вектора с кратчайший поворот

от первого вектора a ко второму вектору b виден совершающимся против часовой стрелки. В противном случае - тройка левая (рисунок 29).

с

правая тройка

левая тройка

с

b

a

b

a

Рисунок 29

Векторным

произведением

двух неколлинеарных

векторов a и

b

называется вектор, численно равный площади параллелограмма, построенного на векторах a , b ; направленный перпендикулярно плоскости перемножаемых векторов и образующих с ними правую тройку.

Векторное произведение векторов a и b обозначается a ×b или [a,b ]

Рисунок 30

Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j, k (рисунок 31)

145

[i , j]= k , [j, k ]= i , [k , i ]= j .

Рисунок 31

Свойства векторного произведения векторов

1. Модуль векторного произведения двух векторов равен произведению длин этих векторов на синус угла между ними.

Рассмотрим два неколлинеарных вектора a, b и отложим их от произвольной точки O (рисунок 32).

Рисунок 32

Построим параллелограмм на этих векторах как на сторонах. Найдем площадь параллелограмма OACB :

SOACB = OA OB sin AOB =	a		b				sin a, b .

Поскольку, модуль векторного произведения двух неколлинеарных векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах, то

[a , b ]

=

a

b

sin a,b .

2. Для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нуль-вектору, то есть

[a, b ]= 0 .

Действительно, если

a и

коллинеарны, то sinϕ = 0 . Следовательно,

b

[a,

]

=

a

sin ϕ = 0 , т.е.

длина вектора [a,

] равна нулю, а значит, вектор

b

b

b

[a, b ]является нуль-вектором.

3. Векторное произведение двух неколлинеарных векторов антикоммутативно, то есть

146

[a,b ]= −[b ,a].

Действительно, если векторы a и b коллинеарны, то свойство очевидно. Пусть a и b неколлинеарны. Из определения векторного произведения следует, что векторы [a, b ] и [b , a ] имеют одинаковые длины (длина векторного произведения не зависит от порядка сомножителей), коллинеарны (они перпендикулярны одной и той же плоскости в которой лежат векторы a и b ), но

направлены противоположно, так как

если, например, векторы a, b , [a, b ]

образуют правую тройку, то векторы a,

, [

,

]. Следовательно. [a,

]= −[

,a].

b

b

a

b

b

4.Числовой множитель можно выносить за знак векторного

произведения, то есть

[λ

,

]= λ[

,

]

(λ R) или [

,α

]= α[

,

] (α R).

b

b

b

b

a

a

a

a

5. Векторное

произведение векторов дистрибутивно относительно

операции сложения векторов, то есть

[a + b , c ]= [a, c ] + [b , c ].

Доказательство 3 и 4 свойств предлагаем читателю выполнить самостоятельно.

6.Выражение векторного произведения через координаты.

Результаты векторного произведения базисных векторов занесем в таблицу:

i

j

k

−

i

0

k

j

−

j

k

0

i

− i

k

j

0

Рисунок 33

Чтобы не ошибиться со знаком, удобно пользоваться схемой (рисунок 33): если направление кратчайшего пути от первого вектора ко второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает – третий вектор берется со знаком «минус».

Пусть даны два векторы a = a1i + a2 j + a3 k и b = b1i + b2 j + b3 k . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно

свойствам векторного произведения):

[a,

]= [(a1i

+ a2

+ b2

)]=

b

+ a3 k

+ b3 k

j

), (b1i

j

= a1b1 [i

]+ a1b2

[i

,

]+ a1b3 [i

]+ a2b1 [

]+ a2b2 [

,

]+ a2b3 [

]+

, k

, k

, i

j

j

, i

j

j

j

+ a3b1 [k

]+ a3b2 [k

,

]+ a3b3 [k

]=

, i

j

, k

0

+ a1b2 k

− a1b3

j

− a2b1k +

0

+

+ a3b1

+

0

+ a2b3i

j

− a3b2i

= (a2b3 − a3b2 )i

− (a1b3 − a3b1 ) j +

+ (a b

− a

a2

a3

a1

a3

+

a1

a2

b )k

=

−

k

.

2

2

i

j

1

1

b2

b3

b1

b3

b1

b2

Полученную формулу можно записать еще короче:

147

[a ,

]=

i

j

k

a1

a2

a3

,

(6.8)

b

b1

b2

b3

так как правая часть предыдущего равенства соответствует разложению определителя третьего порядка по элементам первой строки.

Например, вычислим площадь параллелограмма, построенного на векторах a ={6,3,−2},b ={3,−2,6}.

Решение. Находим векторное произведение векторов a, b , используя (6.8):

[a,		]=	i				j		k						3	− 2				6	− 2				6	3
			6			3 − 2
	b																					+ k
												= i			− 2	6	− j			3	6				3	− 2	=14i − 42 j − 21k .
			3			− 2			6

Так как модуль векторного произведения двух векторов равен площади построенного на них параллелограмма, то

Sпар = [a, b ] = 142 + (−42)2 + (−21) 2 = 49 (кв.ед.).

Таким образом, площадь искомого параллелограмма равна 49 квадратным единицам.

6.8 Смешанное произведение трех векторов и его свойства

Смешанным произведением трех векторов a, b , c называется число,

обозначаемое (a,

, c ) и равное скалярному

произведению вектора a

на

b

векторное произведение векторов

и c , то есть

b

(

,

,

)=

[

,

].

(6.9)

b

b

a

c

a

c

Пусть относительно ортонормированного базиса {i

,

} векторы a,

, c

, k

b

j

имеют координаты a ={a1, a2 , a3},

={b1, b2 , b3},

c ={c1, c2 , c3}.

b

Смешанное произведение трех векторов, заданных своими координатами в ортонормированном базисе, равно определителю третьего порядка, составленному из их координат, то есть

				a1	a2	a3
(a ,		,	c	)= b1	b2	b3 .	(6.10)
	b

c1 c2 c3

Справедливость (6.10) следует из координатного представления скалярного произведения векторов и правила нахождения координат векторного произведения. (Предлагаем доказательство формулы (6.10) выполнить читателю самостоятельно.)

Теорема 6.2. Смешанное произведение векторов равно нулю (a, b , c )= 0 тогда и только тогда, когда либо векторы a, b , c компланарны, либо хотя бы один вектор нулевой.

148

Доказательство. Действительно, если векторы a, b , c компланарны, то

они линейно зависимы. В этом случае определитель, составленный из координат векторов, равен нулю, поэтому равно нулю смешанное произведение векторов. Если среди векторов один нулевой, то произведение равно нулю по определению.

Обратно, если смешанное произведение векторов равно нулю, то равен нулю определитель, составленный из координат векторов. Последнее означает

линейную зависимость векторов a, b , c . Векторы a, b , c становятся

компланарными, в частности, какие-то из этих векторов могут быть нулевыми.

Следовательно, условие компланарности трех векторов в координатной форме имеет вид:

a,

c

a1

a2

a3

,

компланарны

b1

b2

b3

= 0 .

b

c1

c2

c3

a = {2,5,7},

= {1,1,−1},

c = {1,2,2}

Например, покажем, что

векторы

b

компланарны.

Решение. Находим смешанное произведение векторов:

2

5

7

1

−1

1 −1

1 1

(a,

, c )=

1 1 −1

= 2

− 5

+ 7

= 8 −15 + 7 = 0.

b

1

2

2

2

2

1

2

1

2

Так как (a,

, c )= 0 , то заданные векторы компланарны.

b

Теорема 6.3 Смешанное произведение (a,

, c ) равно объему

b

параллелепипеда, построенного на векторах a,

,

c , взятому со знаком «+», если

b

тройка a,

, c - правая, со знаком «-», если тройка a,

, c - левая.

b

b

Доказательство.

Пусть

даны

некомпланарные

векторы

a,

, c ,

b

образующие правую тройку. Обозначим через V объем параллелепипеда, построенного на этих векторах, через S – площадь параллелограмма,

построенного на векторах b , c , а через h – высоту параллелепипеда (рисунок 34).

Рисунок 34

Тогда по определению скалярного и векторного произведений имеем: a [b , c ]= a [b ,c ]cos θ = a b c sinϕcos θ =

= b c sinϕa cos θ,

149

где ϕ - угол между векторами

, c , а θ

- угол между векторами a и [

, c ]. Так

b

b

как

c

sin ϕ = S,

a

cosθ = h , то a [

,

c ]= Sh =V . Если тройка a,

, c - левая,

b

b

b

то h =

a

cos(π −θ)

=

−

a

cosθ . Поэтому a [

, c ]= −Sh = −V .

b

Свойства смешанного произведения векторов

1. Смешанное произведение векторов не изменяется при круговой перестановке векторов-сомножителей, то есть

(a, b , c )= (c, a, b )= (b , c, a ).

Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.

2.

Смешанное произведение меняет знак на противоположный, если

поменять местами любые два сомножителя, то есть

(

,

)= −(

,

,

).

b

,

b

a

c

a

c

3.

Числовой

множитель

можно выносить

за знак

смешанного

произведения, то есть

(λ

,

,

)= λ(

,

,

) (λ R).

b

b

a

c

a

c

Действительно,

обозначим

[

, c ]= е

и

используя

свойство

b

ассоциативности скалярного произведения относительно умножения на число, получим

(λa, b , c )= (λa)[b , c ]= (λa)e = λ(ae) = λ(a, [b , c ]) = λ(a, b , c ).

4.

Смешанное

произведение

векторов

дистрибутивно относительно

сложения векторов, то есть

(

+

,

,

)= (

,

,

)+ (

,

).

b

d

d

b

, d

a

c

a

c

c

]= е,

Действительно,

обозначим

[c,

тогда используя свойство

d

дистрибутивности скалярного произведения, имеем

(a + b , c, d )= ((a + b ),[c, d ]) = (a + b )e = ae + b e =

= (a,[c, d ]) + (b ,[c, d ]) = (a, c, d )+ (b , c, d ).

5. Геометрический смысл модуля смешанного произведения трех некомпланарных векторов: модуль смешанного произведения трех

некомпланарных векторов численно равен объему параллелепипеда, построенного

на этих векторах, отложенных от одной точки, как на ребрах, то есть

(a ,

,

c

)

=Vпар−да.

(6.11)

b

Таким образом,

V

=

1 V

=

1

(a ,

,

)

,

b

c

призмы

2

пар

−да

2

V

=

1 V

=

1

(a ,

,

c

)

.

тетраэдра

пар−да

b

6

6

150

6.9 Вопросы для самоконтроля

1Сформулируйте определение вектора.

2Какие векторы называются коллинеарными?

3Какие два вектора называются равными?

4Объясните суть правила сложения векторов.

5Какие три вектора называются компланарными?

6Дайте определение проекции вектора на ось.

7Чему равна проекция суммы нескольких векторов на ось?

8Является ли вектор a = a1 − a2 линейной комбинацией системы векторов

a1, a2 , a3 ?

9Сформулируйте определение линейнозависимой системы векторов.

10Сформулируйте определение линейно независимой системы векторов.

11Верно ли утверждение: любые пять векторов в трехмерном пространстве линейно зависимы?

12Сформулируйте определение максимально линейно независимой системы векторов.

13Дайте определение базиса системы векторов.

14Что означает базис на плоскости; в пространстве?

15Что означает координаты вектора в базисе {e1, e2 , e3}?

16Как сложить (вычесть) два вектора, заданные своими координатами в некотором базисе? Как умножить вектор на число?

17Напишите необходимое и достаточное условие коллинеарности двух векторов. Как оно записывается в координатной форме?

18Какие два вектора называются ортогональными?

19Какой базис в пространстве называется ортонормированным?

20Дайте определение скалярного произведения двух ненулевых

векторов.

21Как найти скалярное произведение двух векторов по их координатам в ортонормированном базисе?

22Если угол между векторами 90o, чему равно скалярное произведение этих векторов?

23Напишите формулу для определения угла между двумя векторами.

Может ли угол между векторами равняться: 0 o ; 45 o ; 180 o ; 270 o ?

24Какая тройка векторов называется правой, левой?

25Дайте определение векторного произведения двух неколлинеарных векторов. Перечислите основные свойства векторного произведения.

26Запишите формулу для нахождения векторного произведения векторов, заданных своими координатами.

27Дайте определение смешанного произведения трех векторов.

28Чему равно смешанное произведение трех векторов, если известны их координаты в ортонормированном базисе?

29Сформулируйте условие компланарности трех векторов.

30Как найти объем тетраэдра, построенного на трех векторах как на

ребрах?

151