
- •Введение
- •Глава 1 Первоначальные сведения об основных алгебраических структурах
- •Глава 2 Комплексные числа
- •Глава 3 Многочлены одной переменной
- •Глава 4 Матрицы и определители
- •Глава 5 Системы линейных уравнений
- •Глава 6 Векторная алгебра
- •Глава 7 Аналитическая геометрия на плоскости
- •Глава 8 Аналитическая геометрия в пространстве
- •Глава 9 Линейное пространство. Подпространство линейного пространства
- •Глава 10 Евклидово и унитарное пространство
- •Глава 12 Квадратичные формы
- •Глава 13 Геометрические объекты дифференциальной геометрии
- •Глава 14 Аналитическое изображение поверхностей и их образование
- •Глава 15 Топология
- •Список использованных источников

Глава 15 Топология
15.1 Что такое топология?
Что касается меня, то все различные пути, на которых я последовательно находился, приводили меня к Analysis situs.
А. Пуанкаре
Топология как наука сформировалась, по общему мнению, в трудах великого французского математика Анри Пуанкаре в конце XIX в. Первые наблюдения топологического характера восходят к Л. Эйлеру и К. Гауссу. Начало топологических исследований можно отнести к работам Б. Римана (середина XIX в.). В его исследованиях по теории функций были развиты новые методы, основывающиеся на геометрических представлениях. Б. Риманом была сделана попытка сформулировать понятие многомерного многообразия и ввести высшие порядки связности. Эти понятия были уточнены Э. Бетти (1871). Но только А. Пуанкаре, исходя из потребностей теории функций и дифференциальных уравнений, ввел целый ряд важнейших топологических понятий, развил содержательную теорию и применил ее к исследованиям в различных разделах математики и механики. Его идеи и поставленные им проблемы до сих пор существенно влияют на развитие топологии и ее приложений.
А. Пуанкаре так определял содержание Analysis situs* (как тогда называли топологию): «Analysis situs есть наука, которая позволяет нам узнавать качественные свойства геометрических фигур не только в обычном пространстве, но также и в пространстве более трех измерений. Analysis situs в трех измерениях является для нас познанием почти интуитивным; напротив, Analysis situs в более чем трех измерениях представляет громадные трудности, и чтобы начать пытаться их преодолевать, нужно быть очень убежденным в крайней важности этой науки. Если эта важность не всеми понята, то это потому, что об этом недостаточно размышляли».
Чтобы уяснить, что понимается под качественными свойствами геометрических фигур, представим себе сферу в виде резиновой оболочки и разрешим сжимать и растягивать ее любым способом без разрывов и не «склеивающим» различные ее точки в одну. Такие преобразования сферы называются гомеоморфизмами, а различные фигуры, получающиеся при гомеоморфизмах, - гомеоморфными между собой. Так вот, качественные свойства сферы – это свойства, общие всем гомеоморфным ей фигурам, или, как говорят, сохраняющиеся при гомеоморфизмах.
Очевидно, можно говорить о гомеоморфизмах и качественных свойствах и других фигур. Качественные свойства принято также называть
* Analysis situs – геометрия положения (перевод с латинского), этот термин как название дисциплины ввел Б.Риман; термин «топология» (от греч. τοπος - место, λογος - закон) ввел И.Б. Листинг (1847).
348
топологическими. В данном примере очевидно такое топологическое свойство сферы, как ее целостность (связность). Более глубокие свойства обнаружатся при попытке установить гомеоморфизм сферы, например, с кругом (или с шаром). Легко прийти к убеждению, что такой гомеоморфизм невозможен. Однако чтобы доказать это, необходимо указать различные топологические свойства для сферы и круга (шара). Такими свойствами являются «стягиваемость» круга (шара) в одну из своих точек посредством «плавного» его изменения, сжатия по радиусам к центру и «нестягиваемость» сферы по себе ни к одной из своих точек. Полезно обратить внимание и на топологическое различие между волейбольной и велосипедной камерами. Эти интуитивные представления нуждаются в строгом обосновании.
Исследования Пуанкаре дали начало одному из направлений в топологии –
комбинаторной, или алгебраической топологии. Ее метод заключается в сопоставлении геометрическим фигурам по некоторому, общему для всех фигур, правилу алгебраических объектов (групп, колец и т. п.) так, что определенным отношениям между фигурами соответствуют алгебраические отношения между объектами. Изучение свойств алгебраических объектов проливает свет на свойства геометрических фигур. Алгебраические объекты, построенные А. Пуанкаре, суть группы гомологии и фундаментальная группа.
Развитие метода алгебраической топологии неизбежно привело к объединению с теоретико-множественными идеями. Действительно, исследование качественных свойств множеств в пространствах любого числа измерений в дальнейшем вылилось в понятие топологического пространства – фундаментальное понятие, пронизывающее всю математику. Оно связано не только с рассмотрением геометрических фигур в конечномерных пространствах: развитие теории функции действительного переменного и функционального анализа привело к построению функциональных пространств, которые, как правило, бесконечномерны.
Топологические пространства и их непрерывные отображения, изучение их общих свойств составили содержание одного из разделов топологии, известного под названием «общая топология».
Приведем некоторые задачи, стимулировавшие топологические исследования.
Если S1 – окружность на евклидовой плоскости R2 , то множество R2 \ S1
распадается на два взаимно дополнительных открытых множества: внутренность A и внешность B по отношению к S1 . Окружность S1 играет роль перегородки
между A и B . Можно ли провести непрерывный простой путь из произвольной точки a A в произвольную точку b B так, чтобы он не пересекал перегородку
S1 (Простым непрерывным путем, называют гомоморфное отображение отрезка [0, 1] числовой оси в плоскость.) Ответ отрицателен. Действительно, если
ρ(x, |
y) - евклидово расстояние между точками x , |
y плоскости R2 и γ(t) – такой |
|
путь, |
0 ≤ t ≤1, γ(0)= a , γ(1)= b , то |
функция |
f (t)= p(γ (t), 0) где 0 – центр |
окружности, непрерывна и f (0) < r , |
f (1) > r , где r – радиус окружности S1 . По |
||
349
свойству непрерывных функций f (t) принимает значение r в некоторой точке t0 ,
следовательно, γ(t0 ) S1 .
Заменим теперь окружность S1 ее гомеоморфным образом Γ (такая кривая называется простои замкнутой). Возникает вопрос: разбивается ли множество
R2 \ Γ на непересекающиеся открытые множества, границей каждого из которых является Γ? Ответ утвердительный (теорема Жордана), но доказательство уже использует тонкие топологические понятия. При этом кривая Γ так же, как и S1
обладает свойством перегородки, разделяющей два открытых множества.
Задача еще более усложнится, если вместо простой замкнутой кривой рассмотреть гомеоморфный образ n -мерной сферы, лежащий в (n +1)-мерном евклидовом пространстве. Обобщение теоремы Жордана на этот случай было дано Л. Э. Брауэром в 1911—1913 гг. Глубокое обобщение этого результата привело к созданию теорем двойственности (Дж. У. Александер, Л. С. Понтрягин, П. С. Александров и др.,) долгое время определявших развитие алгебраической топологии.
Другая важная задача – обобщение понятия размерности. Размерность евклидова пространства хорошо известна как алгебраическое понятие. Является ли оно топологическим свойством, т. е. будут ли гомеоморфные евклидовы пространства иметь одинаковую размерность? Положительный ответ был дан А. Лебегом (1911).
Что же касается геометрических фигур, лежащих в евклидовых пространствах, то следует первоначально сформулировать для них понятие размерности. Идея такого определения была высказана еще А. Пуанкаре. Размерность пустого множества полагается равной −1, и далее по индукции: если мы уже знаем, что такое размерность до n −1, то размерность n некоторого множества A ( dim A = n ) означает, что его можно разбить на сколь угодно мелкие части множеством размерности n −1 и нельзя этого сделать множеством размерности n − 2. Эти идеи получили уточнение и развитие в работах Л. Э. Брауэра, К. Менгера, П. С. Урысона, П. С. Александрова и др.
Еще одно важное направление в топологии, тесно связанное с приложениями, - теория неподвижных точек. Уже в алгебре и началах анализа мы
встречаемся с вопросом существования решений уравнений вида |
|
f (x) = 0 , |
(15.1) |
где f (x) – многочлен или более сложная функция. Уравнение (15.1) эквивалентно
уравнению |
|
f (x) + x = x , |
(15.2) |
или (обозначив F(x) = f (x) + x уравнению |
|
F(x) = x . |
(15.3) |
Решения уравнения (15.3) называются неподвижными точками отображения F . Если уравнение (15.1) векторное, т. е. представляет собой систему из n уравнений с n неизвестными, n >1, то эквивалентное уравнение (15.3) тоже векторное и, следовательно, неподвижные точки лежат в многомерном
евклидовом пространстве Rn .
350
Чрезвычайно важной задачей является отыскание достаточно общих и эффективных признаков существования неподвижных точек. Л. Э. Брауэром получен замечательный результат, находящий широчайшие приложения в современных исследованиях. Он формулируется удивительно просто: всякое непрерывное отображение выпуклого ограниченного замкнутого множества в себя имеет неподвижную точку. Выпуклое множество может рассматриваться как в трехмерном, так и в многомерном евклидовом пространстве. Например, непрерывное отображение в себя замкнутого (т. е. рассматриваемого вместе с границей) круга в плоскости или шара в пространстве обязательно имеет неподвижную точку.
Подчеркнем, что задачи, описанные выше, далеко не составляют всей проблематики топологии. Приведем другие примеры. В работах Б. Римана впервые было введено понятие n -мерного многообразия как пространства, в
котором точки обладают n числовыми координатами, определенными, по крайней мере, на достаточно малых участках пространства. В современной математике различают топологические и гладкие многообразия. Это связано с теми или иными возможностями согласования систем координат, заданных на отдельных участках многообразия. Участки многообразия могут пересекаться, и пересечения получают, таким образом, различные системы координат, при этом каждая система координат может быть выражена через другую, непрерывным или гладким (дифференцируемым) преобразованием. В первом случае многообразие называют топологическим, во втором – гладким.
Являясь обобщением понятия поверхности в трехмерном евклидовом пространстве, понятие многообразия охватило целый ряд геометрических объектов, возникавших в классической механике, дифференциальных уравнениях, теории поверхностей. Пуанкаре придал окончательную форму понятию многообразия и развил начала анализа на таких пространствах.
Накопление различных алгебраических объектов в топологии привело к выделению и развитию «гомологической алгебры». В 30-40-е годы нашего столетия возникла из дифференциальной геометрии и развилась в самостоятельное направление теория расслоенных пространств (расслоений).
Расслоенное пространство можно представить как непрерывную совокупность пространств – слоев, гомеоморфных друг другу и «занумерованных» точками другого пространства – базы расслоения. Простейший пример – совокупность нормалей или касательных плоскостей к двумерной поверхности в евклидовом пространстве (базе расслоения). Однако в общем случае и слои, и база расслоения могут быть устроены значительно сложнее.
В частности, развитие топологии привело к решению ряда стоявших перед топологами крупных проблем: создание Ж. Лере фундаментального алгебраического метода вычисления гомологических групп с помощью спектральной последовательности; полное решение М. М. Постниковым проблемы определения гомотопического типа пространств; исследование числа «гладких структур» на данном топологическом многообразии (т. е. способов превратить его в гладкое многообразие. Исследована проблема триангуляции гладких многообразий, т. е. возможности их разбиения на правильно
351
примыкающие симплексы. Фигуры, составленные из симплексов (так называемые полиэдры), рассматривал, еще А. Пуанкаре при построении теории гомологии. Поясним, симплекс – это выпуклая оболочка линейно независимых точек в евклидовом пространстве или ее гомеоморфный образ; указанные точки называются вершинами симплекса, а уменьшенное на единицу их число – размерностью симплекса. Всякое подмножество вершин симплекса также определяет симплекс – грань исходного симплекса; правильное примыкание симплексов в полиэдре означает, что симплексы могут пересекаться только по их обшей грани. Один из принципиальных вопросов классической топологии: допускают ли два гомеоморфных полиэдра размерности n «одинаковые», с комбинаторной точки зрения, триангуляции? Эта, так называемая, «основная проблема комбинаторной топологии» была решена для размерности n < 3. Б. Е. Мойсом, а для старших размерностей она решается, вообще говоря, отрицательно (случай n = 4 удалось исследовать лишь в 80-е годы – М. Фридман, С. Дональдсон); С. П. Новиков, Р. Керби, Л. Зибенман исследовали возможное число неэквивалентных триангуляции многообразия.
Подробности развития топологии читатель может найти в цитировавшейся выше «Истории отечественной математики» (см. список использованных источников).
К настоящему времени топология стала мощным инструментом математического исследования, а ее язык приобрел универсальное значение.
Замечательным фактом является возникновение в 70-80-е годы XX века комплекса приложений топологии в современной физике – факт, значимый не только для физики, но и для самой топологии. «В ряде случаев без топологических понятий оказалось невозможным понять суть реальных физических явлений... Топология нашла себе ряд блестящих применений в самых разнообразных задачах для описания качественных, устойчивых свойств различных математических и физических объектов...»
Естественно отметить и обратное – влияние физических проблем на развитие топологии. Академик С. П. Новиков, энергично пропагандирующий взаимосвязи топологии и физики и активно участвующий в развитии этого направления, выразил еще в 1997 году уверенность, что в «… XXI веке топология станет необходимым инструментом приложений к анализу, с которым должен быть знаком каждый».
15.2 Обобщение понятий пространства и функции
1. Метрическое пространство. Как уже говорилось, в топологии выработано существенно более широкое понятие пространства, чем евклидово. Вначале мы сделаем первый шаг и рассмотрим понятие метрического пространства (менее общее, чем понятие топологического пространства). Это вызвано как большей простотой, так и широким использованием этого понятия в современной математике.
В евклидовом пространстве R3 для каждой пары его точек x = (ξ1, ξ2 , ξ3 ),
352
y = (η1, η2 , η3 ) определено расстояние
ρ(x, y)= ∑n (ξi −ηi )2 1/ 2 .
i =1
При изучении R3 существенно используются следующие свойства расстояния:
I ρ(x, y)≥ 0 для любых x , y .
II ρ(x, y)= 0 тогда и только тогда, когда x = y .
III ρ(x, y)= ρ(y, x).
IV ρ(x, y)≤ ρ(x, z)+ ρ(z, y)для любых x, y, z R3 (неравенство треугольника).
На R3 могут существовать и другие вещественные функции от пары точек x , y , удовлетворяющие свойствам I – IV.
Пример 1. Пусть (ξ , ξ |
2 |
, ξ |
3 |
), |
(η , η |
2 |
, η |
3 |
) – |
координаты точек x, y R3 . |
|||
1 |
|
|
1 |
|
|
|
|
|
|
||||
Можно показать, что функция ρ(x, y)= max |
|
ξi |
−ηi |
|
удовлетворяет свойствам I – |
||||||||
|
|
||||||||||||
IV. |
|
|
|
|
1≤i≤3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Такие функции могут существовать также и на множествах иной природы. Пример 2. Пусть X - произвольное множество. Положим ρ(x, y)= 0 , если
x и y - совпадающие элементы в X , и ρ(x, y)=1 в противном случае. Очевидно, что такая функция ρ также удовлетворяет свойствам I – IV.
Функции ρ из этих примеров естественно назвать расстояниями между элементами соответствующих множеств.
Чтобы ввести общее понятие расстояния, напомним определение произведения двух множеств. Если X и Y - два множества, то их произведением X ×Y называют множество, состоящее из всех упорядоченных пар (x, y), где
x X , y Y . В частности, определена произведение X × X .
Множество |
X вместе с отображением ρ : X × X → R1 |
(в числовую ось), |
сопоставляющим |
каждой паре (x, y) X ×Y вещественное |
число ρ(x, y) и |
удовлетворяющим свойствам I – IV, называется метрическим пространством и обозначается (X , ρ).
Отображение ρ называют расстоянием или метрикой пространства X . Элементы множества X называют обычно точками.
Всякое множество можно превратить в метрическое пространство, наделив его метрикой, описанной в примере 2. Такое метрическое пространство называется дискретным. Однако такой способ «метризации» малосодержателен.
Например, пусть X R3 – подмножество евклидова пространства. Расстояние в R3 в то же время может служить расстоянием в X . Метрика в X
получается в этом случае сужением метрики в R3 .
Если (X , ρ) - метрическое пространство и Y X – подмножество, то
353
(Y , |
|
) - также метрическое пространство, где |
|
: Y ×Y → R1 - сужение |
ρ |
ρ |
|||
отображения ρ на подмножество Y ×Y . |
|
|
||
|
|
Говорят, что метрика в Y индуцируется |
(является наследственной) |
|
метрикой из X , а Y называют подпространством метрического пространства
X .
Ряд примеров метрических пространств естественно возникает в задачах анализа.
Например, рассмотрим множество всех непрерывных функций на отрезке [0, 1]. Его обычно обозначают C[0, 1]. Если x(t), y(t) - две непрерывные функции
из C[0, 1], то положим |
|
|
|
|
|
ρ(x, y)= max |
|
x(t)− y(t) |
|
. |
(15.4) |
|
|
||||
t [0; 1] |
|
|
|
|
|
|
|
|
|
|
|
Предлагаем читателю самостоятельно доказать, что функция (15.4) является метрической.
Множество C[0, 1] с описанной выше метрикой называется пространством непрерывных функций; оно играет важную роль в анализе.
2. Сходящиеся последовательности и непрерывные отображения. В
метрическом пространстве (X , ρ) естественно вводятся понятия, обобщающие
начальные понятия математического анализа. |
|
|
|
|
|
||||||
Отображение |
n → xn |
множества натуральных чисел |
в метрическое |
||||||||
пространство (X , ρ) называется последовательностью точек этого |
|||||||||||
пространства и обозначается {xn }. |
|
|
|
|
|
|
|||||
Говорят, |
что |
последовательность {xn } сходится к точке a (имеет |
|||||||||
предел a ), если для всякого ε > 0 найдется натуральное число n0 (ε ) такое, что |
|||||||||||
ρ(xn , a)< ε для всех n ≥ n0 (ε). |
|
|
|
|
|
|
|
||||
Этот факт часто записывают так: |
|
|
|
|
|
||||||
ρ |
|
|
|
или, проще, |
xn → a . |
|
|
|
|||
xn →a , |
|
|
xn (t), |
0 ≤ t ≤1, |
|||||||
Рассматривая последовательность непрерывных функций |
|||||||||||
как последовательность в метрическом пространстве C[0, 1], |
можно говорить о |
||||||||||
сходимости этой последовательности к элементу |
|
|
ρ |
|
|||||||
x0 = x0 (t): xn →x0 . Такая |
|||||||||||
сходимость часто называется равномерной на отрезке [0, 1]. |
|
|
|
||||||||
Определим |
понятие |
непрерывного |
отображения |
метрического |
|||||||
пространства |
(X , ρ1 ) в метрическое пространство (Y , ρ2 ). |
|
|
|
|||||||
Пусть |
f : X →Y |
- отображение множества |
X в множество Y . Если для |
||||||||
всякой точки |
x0 X |
и всякой |
последовательности |
|
ρ1 |
в X |
|||||
xn →x0 |
|||||||||||
последовательность |
образов |
в Y |
сходится |
к |
|
|
ρ2 |
(x0 ), то |
|||
f (x0 ): f (xn ) → f |
|||||||||||
отображение |
f |
называется |
непрерывным |
отображением |
метрического |
||||||
пространства (X , ρ1 ) в метрическое пространство (Y , ρ2 ). |
|
|
|||||||||
354
Если свойство непрерывности, выраженное этим определением, рассмотреть в фиксированной точке x0 , то получим определение непрерывного
отображения в точке x0 .
Очевидно, что это определение является обобщением понятия непрерывной числовой функции; оно охватывает широкий класс отображений геометрических фигур в евклидовых пространствах.
Эквивалентное определение непрерывного отображения метрических
пространств можно дать и на языке ε , δ : |
|
|
|
|
||||
отображение |
f : X →Y непрерывно, если для любого x0 X и любого |
|||||||
ε > 0 найдется такое δ =δ(ε, x0 ), что ρ2 (f (x), f (x0 ))< ε , как только ρ1(x, x0 )<δ . |
||||||||
Если |
в |
этом |
определении δ не |
зависит от |
выбора |
точки x0 , то |
||
отображение f |
называется равномерно непрерывным. |
|
|
|||||
Напомним, |
что |
отображение |
множеств |
f : X →Y |
называется |
|||
сюръективным, если каждый элемент из Y |
является образом некоторого |
|||||||
элемента из |
X ; инъективным, если различные элементы из X отображаются в |
|||||||
различные |
элементы |
из |
Y ; биективным, |
если |
отображение сюръективно и |
|||
инъективно одновременно.
Теперь мы подошли к определению гомеоморфизма метрических
пространств. |
f : X →Y |
|
|
|
Отображение |
метрических |
пространств |
называется |
|
гомеоморфизмом, а пространства X , Y - гомеоморфными, если 1) |
f биективно, |
|||
2) f непрерывно, 3) обратное отображение f −1 непрерывно. |
|
|||
Это определение уточняет то представление о гомеоморфных фигурах, которое на интуитивном уровне обсуждалось в параграфе 15.1. Таким образом, получает твердую почву и понятие о топологических свойствах фигур.
Топологическими свойствами метрических пространств называются такие свойства, которые сохраняются при гомеоморфизмах.
Гомеоморфные метрические пространства называют топологически эквивалентными.
Если отображение f : X →Y является гомеоморфизмом на свой образ f (X ), рассматриваемый как подпространство в Y , то f называют вложением
пространства X в Y .
Если X Y , то имеется естественное вложение X в Y : f (x) = x .
15.3 От метрического пространства к топологическому
1 Метод «склейки». Обсудим идею введения более общего понятия пространства, чем метрическое, - понятия топологического пространства – и дадим первоначальное представление о таких пространствах. Сначала опишем прием построения новых пространств, который сразу выводит нас за рамки метрических пространств.
Пусть (X , ρ) - некоторое метрическое пространство (можно для
355

наглядности представлять себе X |
как некоторое подмножество евклидова |
|
пространства R3 ). Пусть X разбито на непересекающиеся подмножества A : |
||
|
|
α |
X = UAα ; |
Aα ∩ Aβ = , |
ели α ≠ β . |
α |
|
|
Если все точки из X , попадающие в какое-нибудь Aα , назвать эквивалентными и затем «склеить» в одну точку * aα , то получится новое
множество Y = Uaα . Оно называется фактормножеством по данной
α
эквивалентности. Заметим, что Y не является подмножеством X , следовательно, к «пространству» Y метрика ρ , вообще говоря, не имеет никакого отношения.
Путем склейки можно получить ряд известных поверхностей в евклидовом пространстве. Рассмотрим некоторые из них. Пусть X - прямоугольник (рисунок 115). Если «склеить» те точки на сторонах ab и cd , которые лежат на общей горизонтали, то получим фактормножество, которое можно отождествить с цилиндром (рисунок 116).
|
|
|
Рисунок 115 |
Рисунок 116 |
Рисунок 117 |
Если «склеить» точки, диаметрально противоположные относительно центра O прямоугольника, лежащие на сторонах ab и cd , то получим «лист Мёбиуса» (рисунок 117).
Можно изготовить модель листа Мёбиуса из листа бумаги, склеив противоположные стороны соответствующим образом. Эта модель наглядно демонстрирует ряд свойств листа Мёбиуса.
Лист Мёбиуса имеет ряд замечательных свойств: у него один край – замкнутая линия adbca , в противоположность цилиндру он имеет одну сторону, так как его можно закрасить непрерывным движением кисти в один цвет, не переходя через край (эти свойства легко наблюдать на бумажной модели). Лист Мёбиуса – неориентируемая поверхность. Напомним, что поверхность ориентируема, если любой достаточно малый кружок на поверхности с фиксированным направлением обхода его границы при любом «плавном» перемещении по поверхности в случае возвращения в исходное положение сохранит первоначальное направление обхода границы (предполагается, что кружок не пересекал край поверхности); в противном случае поверхность неориентируема. Неориентируемость листа Мёбиуса ясна из рисунка 118.
356

Рисунок 118
Если на листе abcd привести склейку сторон ab и cd по точкам, лежащим на общей горизонтали, и одновременно склейку сторон bd и ac по точкам, лежащим на общей вертикали, то получится поверхность, называемая тором (рисунок 119).
Рисунок 119 |
Рисунок 120 |
Если же склеить стороны ab и cd равно как и bd и ac по диаметрально противоположным точкам относительно центра (рисунок 120), то фактормножество не удается реализовать в виде, фигуры в трехмерном евклидовом пространстве. Точнее, такая попытка склеить эквивалентные точки привела бы к поверхности, которая должна пронизывать сама себя без
самопересечений. Мы могли бы поместить эту поверхность в R3 , только разорвав ее на части подходящим образом, но это нарушило бы молчаливо подразумеваемый принцип «непрерывности» склейки (точки, близкие к эквивалентным точкам, при склейке переходят в близкие точки). Полученное
фактормножество называется проективной плоскостью, его обозначают RP2 . Заметим, что прямоугольник abdc гомеоморфен кругу с границей abdc , и
проективную плоскость можно описать иначе – как круг (рисунок 121), у которого склеены диаметрально противоположные точки его границы, или, наконец, как полусферу, диаметрально противоположные точки края которой склеены в одну (рисунок 122).
Рисунок 121 |
Рисунок 122 |
357
Таким образом, операция образования фактормножества в первых трех из рассмотренных случаев приводит снова к фигурам в евклидовом пространстве
R3 , а в последнем случае дает новый объект, не реализуемый в R3 .
2 О понятии топологического пространства. Поясним теперь, как возникает идея топологического пространства. Выше уже отмечалось, что всегда фактормножество естественным образом можно расположить в метрическом пространстве и, следовательно, индуцировать в нем метрику. Одна из функций метрики – характеризовать степень близости двух точек. В определении непрерывного отображения метрика играет именно такую роль. Можно
геометризовать понятие близости, введя в рассмотрение шары |
|
|
||||
Dr (x0 )={x X : ρ(x, x0 )< r}, |
r > 0 , |
|
|
|
||
с центром в |
точке x0 радиуса |
r ; |
тогда точка |
x ε -близка к |
точке x0 , |
если |
x Dε (x0 ). |
|
|
|
|
f : X →Y |
|
Легко |
проверить, что |
непрерывность |
отображения |
двух |
||
метрических пространств можно охарактеризовать следующим эквивалентным способом так: пусть x0 X – произвольная (фиксированная) точка и y0 = f (x0 ) –
элемент Y ; тогда для всякого шара Dε (y0 ) найдется такой шар Dδ (x0 ), что
f (Dδ (x0 )) Dε (y0 ).
Можно сказать, что свойство непрерывности отображения выражается в сохранении близости точек. Понятие близости позволяет точно сформулировать интуитивно данное нами понятие окрестности точки: часть Ω метрического пространства является окрестностью своей точки x0 , если каждая точка,
достаточно близкая к x0 , принадлежит Ω. Таким образом, в метрических
пространствах появляются структуры окрестностей.
«Однако так определенные пространства обладают большим числом свойств, которые можно сформулировать независимо от лежащего в их основе понятия расстояния. Например, каждое подмножество, содержащее окрестность точки x0 , также есть окрестность точки x0 ; пересечение двух окрестностей точки
является окрестностью точки x0 . Эти и некоторые другие свойства влекут массу
следствий, которые выводятся из них совершенно независимо от понятия «расстояние», первоначально легшего в основу определения окрестностей. Так получаются предложения, в которых совсем нет речи о величине, расстоянии и т.
п.»
Если в множестве X не введено расстояние, то понятие близости лишается точного смысла и данное выше определение окрестности непригодно. Однако плодотворным оказывается обратный процесс: для каждого элемента x0 X задать в множестве X некоторую систему подмножеств {Ω(x0 )} так,
чтобы выполнялись основные свойства (аксиомы), объявить их системой окрестностей и назвать элементы из окрестности Ω(x0 ) Ω-близкими к x0 .
Говорят в этом случае, что множество X наделено топологической структурой, или топологией, и называют его топологическим пространством, а элементы
358

X называют точками.
Таким образом, заменяя шары в определении непрерывного отображения окрестностями, получаем понятие непрерывного отображения, а затем и понятие гомеоморфизма топологических пространств. Гомеоморфные топологические пространства называются топологически эквивалентными.
Например, пусть С |
- комплексная плоскость. Расширенная плоскость |
|
комплексного переменного |
~ |
= CU∞ является топологическим пространством: |
C |
||
шаровые окрестности точек z C окрестности точки ∞ вида
Dr (∞)={z C : z > r}U∞,
~
а также подмножества, содержащие их, задают топологическую структуру на C . В метрическом пространстве топологическая структура фактормножества возникает естественным образом из топологической структуры метрического пространства путем склеивания окрестностей. Таким образом, фактормножество
становится топологическим пространством (факторпространством).
3 Склейка двумерных поверхностей. Изучим подробнее факторпространства, получающиеся при склейке плоских фигур. Рассмотрим
многоугольник Π в плоскости R2 и индуцируем в нем метрику из R2 . Очевидно, шаровые окрестности точки x Π состоят из пересечений с Π открытых кругов с центром в точке x . Таким образом, достаточно малые шаровые окрестности точки x - открытые круги, если x не лежит на границе многоугольника, и секторы открытого круга (вместе с ограничивающими радиусами), если x лежит на границе (рисунок 123).
|
|
|
|
Рисунок 123 |
|
|
|
Пусть имеются два многоугольника, Π и Π′; отметим две их стороны, |
a и |
||||
a′. Можно склеить Π и Π′ по этим сторонам, |
задав гомеоморфизм α :a → a′ и |
|||||
объявив |
эквивалентными |
образ и прообраз. |
Топология факторпространства |
|||
(Π Π′)/ R по этой эквивалентности состоит из открытых кругов для внутренних |
||||||
точек |
x Π , |
x′ Π′, из склеившихся секторов для эквивалентных точек x a , |
||||
x′ a′ |
и |
из |
множеств, |
содержащих названные окрестности. Рисунок |
124 |
|
иллюстрирует случай, когда отождествление выполняется соединением многоугольников по равным сторонам a , a′.
359

Рисунок 124
Аналогичным образом можно склеивать две стороны одного многоугольника (см. примеры п. 1).
Рисунок 125
Перейдем к склеиваниям поверхностей. Склеим в пятиугольнике, изображенном на рисунке 125, стороны, обозначенные одинаковыми буквами. Стрелки указывают закон склеивания соответствующих сторон (начало ориентированного отрезка склеивается с началом другого, конец – с концом). Показатель −1 при буквенном обозначении некоторых сторон напоминает о несовпадении для этих сторон направления, задаваемого стрелками, с направлением, задаваемым обходом многоугольника по часовой стрелке. Удобное описание схемы склейки можно получить, записывая последовательно обозначения сторон в «слово», обходя многоугольник по часовой стрелке.
Например, если начинать со стороны a , то схема склейки будет aba−1b−1c . Такая схема характеризует склейку, так как полностью определяет в многоугольнике склеиваемые стороны и закон склеивания. Нетрудно убедиться, что это факторпространство можно получить и другим топологически эквивалентным способом (рисунок 126).
Рисунок 126
Здесь факторпространство представляет тор с вырезом по кривой c (рисунок 127, где штриховыми линиями обозначены линии склейки aa−1 и bb−1 ).
360

Рисунок 127
Top с дырой называется ручкой.
Рассмотрим склейку соседних сторон треугольника. Если ориентации
противоположны, т. е. схема склейки aa−1c (рисунок 128), то факторпространство топологически эквивалентно сфере с дырой (рисунок 129).
Рисунок 128 |
Рисунок 129 |
Рассмотрим склейку соседних сторон с одинаковой ориентацией, т. е. по схеме aac (рисунок 129). Этот треугольник представим как результат склейки двух прямоугольных треугольников по общей высоте d (рисунок 131) с указанной ориентацией. Поменяем порядок склейки этих треугольников: сначала отождествим гипотенузы a , а затем катеты d (рисунок 132). Получится лист Мёбиуса, причем последнее факторпространство гомеоморфно исходному (рисунок 130).
Рисунок 130
361

|
|
|
|
Рисунок 131 |
Рисунок 132 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 133 |
Рисунок 134 |
Теперь, вырезав в сфере S 2 кружок, можно к сфере с дырой приклеить либо ручку, либо лист Мёбиуса по свободному краю c ; последний можно
представлять как окружность S1 (граница вырезанного кружка). В первом случае получаем тор (рисунок 133) (убедитесь в топологической эквивалентности фигур
на рисунке). Во втором – проективную плоскость RP2 . Убедимся в этом. Проективная плоскость топологически эквивалентна факторпространству,
изображенному на рисунке 134. Действительно, остается показать, что верхний «колпачок» (рисунок 134) – лист Мёбиуса с краем c . Представив его как плоское кольцо с отождествлением диаметрально противоположных точек внутренней окружности, выполним топологические преобразования (рисунок 135), приводящие к листу Мёбиуса.
Рисунок 135
Дальнейшие построения можно развивать в двух направлениях:
362
1)вырезать в сфере p кружков и приклеить к ним p ручек;
2)вырезать q кружков и приклеить q листов Мёбиуса. Таким образом
можно получить два ряда поверхностей
M 0 |
, M1 |
, ..., M p ,..., |
(15.5) |
|
N0 , N1, ..., Nq , ... |
||||
|
||||
(очевидно, M 0 и N0 - это сфера S 2 ).
Обсудим свойства этих поверхностей. Прежде всего легко убедиться, что они получены из конечного числа выпуклых многоугольников склейкой их сторон и последующих топологических преобразований. Такие пространства будем называть конечно-триангулируемыми, а разбиение пространства на «криволинейные» многоугольники - триангуляцией. Поверхности M p , Nq
связаны в том смысле, что состоят из единого «куска», не разбиваются на две непересекающиеся группы многоугольников. Это следует из того, что любые две вершины многоугольников триангуляции соединяет непрерывный путь, состоящий из сторон. Рассматриваемые поверхности не имеют края, так как любая граничная сторона многоугольника склеена с другой (в точности с одной) стороной. Отсюда следует, что каждая точка такой поверхности имеет окрестность, гомеоморфную открытому кругу. Такие пространства называются
двумерными многообразиями.
Конечно-триангулируемые связные двумерные многообразия называются замкнутыми поверхностями. Если бы мы клеили не все пары сторон многоугольников, оставив некоторые стороны свободными, то получилась бы
незамкнутая поверхность (или поверхность с краем). Точка на крае имеет
окрестность, |
гомеоморфную |
полукругу. Пример – сфера S 2 |
с несколькими |
|||
дырами. |
|
|
|
M p |
|
|
Отметим |
также, что |
поверхности |
ориентируемы |
и их можно |
||
поместить в |
R3 |
как двусторонние поверхности без самопересечений. Напротив, |
||||
поверхности |
Nq |
неориентируемые (называемые односторонними по аналогии с |
||||
листом Мёбиуса), не допускают вложения в |
R3 |
без самопересечений (но в R4 |
||||
допускают!).
Топологическое пространство, гомеоморфное выпуклому многоугольнику, будем называть топологическим многоугольником. Соответственно образы вершин (сторон) назовем вершинами (ребрами) топологического многоугольника. Без ограничения общности можно считать, что триангуляция поверхности состоит из топологических многоугольников, примыкающих друг к другу ребрами (чтобы этого добиться, нужно выпуклые многоугольники, отождествлением сторон которых получается поверхность, предварительно разбить на достаточно мелкие многоугольники, например треугольники).
Для всякой |
триангулированной поверхности Π |
определим |
число |
χ(Π)= e − k + f , где |
e - число вершин, k - число |
ребер, f - |
число |
многоугольников триангуляции, называемое характеристикой Эйлера поверхности Π. Она обладает замечательным свойством – не зависит от триангуляции, т.е. является топологическим инвариантом поверхности.
Нетрудно доказать топологическую инвариантность характеристики
363
Эйлера χ(S 2 ) для сферы S 2 , если воспользоваться теоремой Жордана*, которая утверждает: всякая простая замкнутая кривая, т.е. кривая гомеоморфная окружности, разбивает сферу или плоскость на две непересекающиеся области,
границей которых она является.
Интересные приложения эйлерова характеристика имеет в теории выпуклых многогранников. Можно представлять поверхность выпуклого многогранника склеенной из конечного числа выпуклых многоугольников (его граней) по тождественным отображениям склеивающихся ребер. Сразу получаем формулу Эйлера для выпуклого многогранника:
α0 −α1 +α2 = 2 ,
где α0 - число вершин, α1 - число ребер, α2 - число граней многогранника. Действительно, слева - эйлерова характеристика поверхности многогранника,
очевидно, гомеоморфной S 2 .
Если в каждой вершине сходятся m граней и каждая грань - выпуклый n - угольник, то говорят, что тип многогранника {n, m}.
Рисунок 136
Если n -угольники правильные, то многогранник называется правильным. Зная тип {n, m}, можно вычислить α0 , α1 , α2 . Действительно, в каждой вершине
сходятся |
m |
ребер, поэтому α0m = 2α1 ; |
в каждой грани - |
n ребер, отсюда |
||||||||||
α2n = 2α1 |
(каждое ребро соединяет две вершины и входит в две грани). Таким |
|||||||||||||
образом, |
|
|
|
|
|
|
α0 −α1 +α2 |
|
|
|
|
4mn |
|
|
|
α0 |
|
= |
α1 |
= |
α2 |
= |
= |
2 |
= |
|
, |
||
|
m−1 |
2−1 |
|
m−1 − 2−1 + n−1 |
m−1 − 2−1 + n−1 |
2n + 2m − mn |
||||||||
|
|
|
n−1 |
|
|
|
||||||||
откуда вычисляются значения α0 , α1 , α2 . Естественное условие положительности α0 , α1 , α2 приводит к неравенству между целыми положительными n , m :
2n + 2m − nm > 0 , |
откуда |
(n − 2)(m − 2)< 4 . |
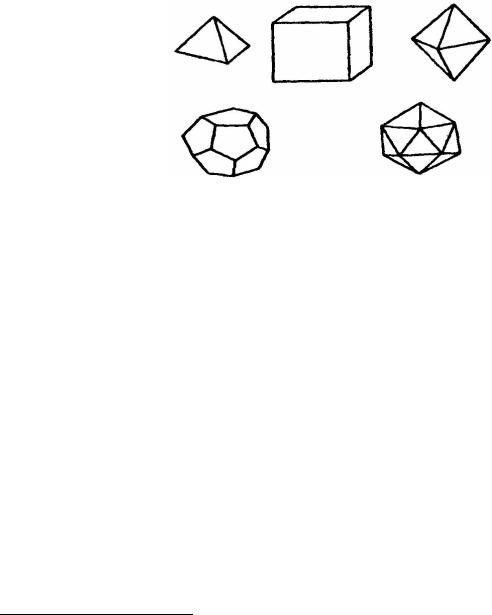
Легко видеть, что имеем всего пять решений: |
||
{3, 3}, {4, 3}, {3, 4}, {5, 3}, {3, 5}. |
(15.6) |
|
В элементарной |
геометрии |
известно пять видов правильных |
многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр (рисунок 136), типы
* Доказательство теоремы Жордана достаточно длинно, и мы его не приводим.
364
которых как раз совпадают с (15.6).
Таким образом, дана полная классификация многогранников типа {n, m}.
15.4 Понятие римановой поверхности
Один из путей, приводящих к основным топологическим понятиям, связан с изучением алгебраических функций и их интегралов; он был открыт Риманом еще в середине прошлого столетия.
Рассмотрим алгебраическое уравнение
a |
0 |
(z)wn + a (z)wn −1 |
+ ... + a |
n |
(z)w = 0 , |
a |
0 |
(z)≠ 0 , |
(15.7) |
|
1 |
|
|
|
|
|
с комплексными коэффициентами, являющимися полиномами от комплексного переменного z , его корни будут функциями w = w(z) от z , при некоторых условиях – аналитическими. Например, если в точке z0 все корни уравнения (15.7) различны, то в окрестности точки z0 существуют n функций wi (z) , i =1,..., n , аналитически зависящих от z .
Аналитическая функция w = w(z), удовлетворяющая уравнению (15.7), называется алгебраической функцией. Уравнение (15.7) определяет несколько ветвей wi (z) алгебраических функций, число которых, вообще говоря, меняется и
которые переходят друг в друга при изменении z . Поэтому говорят о многозначной алгебраической функции w(z) , определяемой уравнением (15.7), и
о ее ветвях wi (z) . Риман выдвинул идею замены z -плоскости С такой поверхностью, на которой функция w(z) будет однозначной, а ее ветви wi (z) будут значениями w(z) на отдельных участках поверхности. Такие поверхности
называются римановыми поверхностями. |
|
|
|
||||
Построить риманову |
поверхность |
нетрудно. Будем рассматривать |
|||||
расширенную |
плоскость |
~ |
= CU∞ |
комплексного переменного |
( z -сферу) и |
||
C |
|||||||
декартово произведение |
С~ ×С~ , состоящие |
из |
упорядоченных |
пар ( z, w ). |
|||
Окрестности в |
С~ ×С~ естественно |
определить |
как декартовы |
произведения |
|||
окрестностей (и все содержащие их множества). Тогда алгебраическое уравнение
(15.7) определяет в С~ ×С~ подмножество – график многозначной алгебраической функции w(z) над комплексной плоскостью С, состоящий из тех пар
( ) ~ × ~ , удовлетворяют уравнению (15.7). Это и есть риманова поверхность z, w С С
Π многозначной алгебраической функции |
w(z) : действительно, проекция |
|
~ |
, задаваемая по правилу |
|
Π → C |
|
|
|
(z, w)→ w , |
(15.8) |
определяет однозначную функцию на римановой поверхности, принимающую значения всех ветвей многозначной функции. Интересен вопрос о строении поверхности Π и о распределении на ней ветвей функции w. Для изучения таких вопросов полезно расширять график Π, присоединяя к Π некоторые «бесконечно
удаленные» точки из С~ ×С~ . Полученное таким образом расширение Π
365

множества Π называют полной римановой поверхностью.
Простейшая многозначная алгебраическая функция связана с уравнением
второй степени |
|
(z)= 0 . |
|
w2 = a (z)w + a |
2 |
(15.9) |
|
1 |
|
|
Замена переменных v = 2w + a1 , приводит это уравнение к более простому виду
v2 − p(z)= 0 , где p(z) |
- многочлен. Поэтому вместо уравнения (15.9) рассмотрим |
||||||
уравнение |
|
|
|
|
|
|
|
w2 − p(z)= 0 . |
|
|
|
|
(15.10) |
||
Пусть p(z)= z . Тогда для алгебраического уравнения |
w2 − z = 0 |
||||||
определена риманова поверхность - график Π1 |
в С~ ×С~ , на котором функция w |
||||||
|
|
|
|
|
~ |
|
- |
однозначна. Присоединив к Π1 точку (∞, ∞), получим «расширение» Π1 |
|
||||||
полную риманову поверхность. |
~ |
|
|
|
|
||
|
~ |
гомеоморфна |
, т.е. двумерной |
сфере S |
2 |
. |
|
Покажем, что Π1 |
C |
|
|||||
Действительно, отображение (15.8) |
|
|
|
|
|
||
w = w(t), |
где |
t = (z, w) Π1, |
|
|
|
|
|
собратным отображением t = (w2 , w) задает, как нетрудно проверить,
гомеоморфизм Π~ 1 , на w-сферу S 2 . Дадим другую конструкцию римановой
поверхности, используемую обычно в теории функций комплексного переменного. Уравнение (15.10) определяет двузначную алгебраическую
функцию w = z . Если z = reiϕ , то два значения ее, w = reiϕ / 2 |
, |
w = − |
reiϕ / 2 , |
1 |
|
2 |
z по |
отличаются знаком и переходят друг в друга при движении |
точки |
||
замкнутому пути, обходящему точку z = 0 . Чтобы предупредить переход ветви w1 в ветвь w2 , проведем разрез на z -сфере вдоль положительной вещественной полуоси (рисунок 137).
Рисунок 137
Этот разрез соединит точки 0 и ∞. К разрезу примыкают два края (берега): ( + ) – верхний, (—) – нижний. Рассмотрим объединение (непересекающееся) двух листов (экземпляров), I и II, разрезанной z -сферы. Объявим лист I носителем ветви w1, II – ветви w2 (полагая wi = ∞ при z = ∞ на каждом листе I, II). На
двулистной поверхности I, II функция w однозначна. Чтобы уловить эффект перехода ветви w1 в ветвь w2 склеим (—) берег I листа с (+) берегом II листа и (+)
берег I листа с (—) берегом II листа. Получим факторпространство Π1′ ,
366

являющееся двулистной римановой поверхностью функции w =  z . Нетрудно усмотреть, что Π1′ гомеоморфно сфере S 2 . На рисунке 138 показана склейка листов I и II после предварительного топологического преобразования их в полусферу путем раздвигания берегов, приводящая к сфере S 2 .
z . Нетрудно усмотреть, что Π1′ гомеоморфно сфере S 2 . На рисунке 138 показана склейка листов I и II после предварительного топологического преобразования их в полусферу путем раздвигания берегов, приводящая к сфере S 2 .
Рисунок 138
Хотя Π1′ и не лежит в R3 (листы I и II пронизывают друг друга, см. схему склейки, рисунок 139), однако наглядно демонстрируется взаимосвязь ветвей w1 и w2 .
Рисунок 139
|
|
Можно |
и непосредственно |
проверить, что |
|
|
|
~ |
, |
||
|
|
отображение w : Π′ → C1 |
|||||||||
задаваемое многозначной функцией |
w = z , также гомеоморфизм на |
w-сферу |
|||||||||
S |
2 |
~ |
Π1′ гомеоморфны между собой и гомеоморфны сфере S |
2 |
. |
|
|
|
|||
|
. Итак, Π1 и |
|
|
|
|
||||||
|
|
|
~ |
~ |
|
и отождествим |
~ |
с S |
2 |
. |
|
|
|
Зададим проекцию Π1 |
→ C формулой z(t)= z |
C |
|
||||||
Имеем диаграммы:
Эти диаграммы коммутативны, т. е. суперпозиция двух отображений (в направлении стрелок) равна третьему отображению (замыкающая стрелка). Горизонтальные отображения в диаграммах - взаимно обратные гомеоморфизмы.
367

Отображение S |
2 |
|
z =w2 |
|
|
2 |
называется двулистным (разветвленным) |
||||||||||||||
|
→S |
|
|||||||||||||||||||
накрытием сферы S 2 |
с точками ветвления z = 0 |
и z = ∞ (проверьте, что обход |
|||||||||||||||||||
точки z =∞ также приводит к изменению ветви). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пусть теперь |
p( z ) = a |
0 |
z2 + a z + a |
2 |
, где |
a |
0 |
, a , a |
2 |
C , |
a2 − 4a |
0 |
a |
2 |
≠ 0 , |
||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
||||||
a0 ≠ 0 . Обозначив через |
r1 и |
r2 |
корни |
|
многочлена |
p( z ), |
r1 ≠ r2 , |
получим |
|||||||||||||
алгебраическую функцию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
w = a0 (z − r1 )(z − r2 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(15.11) |
||||||
Очевидно, она также двузначна. Исследование, аналогичное проведенному выше, показывает, что одна ветвь переходит в другую как при обходе точки r1, так и при
обходе точки r2 , а обход обеих точек (по замкнутому пути, окружающему точки r1 и r2 ), как и точки ∞, не меняет значение ветви. Следовательно, риманова поверхность Π′2 рассматриваемой функции получится из двух экземпляров z -
сферы, разрезанных вдоль отрезка r1r2 , причем берега листов I и II склеиваются так же, как и в первом примере. Заметим, что Π′2 содержит две бесконечно удаленных точки, ∞1 и ∞2 , лежащие на листах I и II и не являющиеся точками ветвления. Очевидно, что пространство по-прежнему топологически
эквивалентно |
|
сфере. Снова имеем двулистное накрытие сферы |
S 2 |
с двумя |
|
точками ветвления z = r1 , |
z = r2 . |
|
w = w(z) |
||
Рассмотрим график Π2 многозначной алгебраической функции |
|||||
над комплексной плоскостью C для алгебраического уравнения |
|
|
|||
w2 − a |
0 |
(z − r )(z − r )= 0 . |
|
(15.12) |
|
|
1 |
2 |
|
|
|
Полезно заметить, |
что если выколоть из C точки r1 и r2 , |
то оставшаяся |
|||
|
|
|
ˆ |
|
|
часть графика Π2 над C \ {r1 , r2 } (обозначим ее Π2 ) гомеоморфна части графика |
|||||
|
|
|
ˆ |
|
|
|
|
Π1 над C \ {0} (обозначим ее Π1 ) Этот гомеоморфизм, как нетрудно проверить, |
|||||||
задается отображением Φ : (z, w)a (ν, τ):, где |
|||||||
τ = |
z − r1 |
, |
ν = |
1 |
|
w |
, |
|
a |
z − r |
|||||
|
z − r |
|
0 |
|
|||
2 |
|
|
|
2 |
|
||
и преобразует уравнение (15.12) к уравнению ν2 − τ = 0 , риманову поверхность Π1 которого мы рассмотрели выше. Однако, если расширение Π~ 1 было получено естественно и просто, то расширение Π~ 2 осуществить более сложно, и мы его не рассматриваем. Однако выше построен его гомеоморфный образ Π′2 .
Таким образом, имеем коммутативную диаграмму
368

(15.13)
(где t = (τ, ν) и где не все отображения являются гомеоморфизмами).
Мы придем к существенно новому результату, если рассмотрим многочлен p( z ) третьей степени. Итак, рассмотрим алгебраическую функцию вида
w = a0 (z − r1 )(z − r2 )(z − r3 ), |
(15.14) |
где r1, r2 , r3 попарно различны. Функция w имеет две ветви, но «соединяются» они между собой более сложным образом. Обход одной точки ri приводит к
изменению ветви функции w, обход любых двух точек сохраняет ветвь, обход всех трех точек, как и обход точки ∞, меняет ветвь. Чтобы «запретить» эти
переходы, достаточно сделать разрезы r1r2 и r3∞ на z -сфере. Тогда каждая ветвь
функции w однозначна на таком листе с разрезами. Чтобы одна ветвь переходила в другую нужным образом, склеим экземпляры I и II соответственно по разрезам
r1r2 и r3∞, причем берега склеиваются, как ранее. Полученное топологическое пространство Π′3 , очевидно, является римановой поверхностью функции (15.14). Существенным отличием поверхности Π′3 от поверхности Π′2 является то, что
она топологически эквивалентна сфере с ручкой (рисунок 140 – здесь разрезы сначала расширяются в «дыры», от них вытягиваются затем трубки, края которых
и склеиваются нужным способом). |
|
|
~ |
2 |
с |
Естественное отображение Π′3 →C является двулистным накрытием S |
|
точками ветвления r1, r2 , r3 , ∞.
Рисунок 140
369

Для функции w =  a0 (z − r1 )(z − r2 )(z − r3 )(z − r4 ), где r1, r2 , r3 , r4 попарно различны, будем иметь риманову поверхность Π′4 , гомеоморфную Π′3 . Это
a0 (z − r1 )(z − r2 )(z − r3 )(z − r4 ), где r1, r2 , r3 , r4 попарно различны, будем иметь риманову поверхность Π′4 , гомеоморфную Π′3 . Это
следует из того, что два разреза, r1r2 и r3r4 , разделяют однозначные ветви и точка r4 играет роль точки ∞ предыдущего примера (последняя не является точкой
ветвления).
Несложно исследовать и случай алгебраической функции
w = a0 (z − r1 )...(z − rn ), |
(15.15) |
где ri попарно различны между собой. На z -сфере делаем n / 2 разрезов r1r2 , …,
rn−1rn , если n четно, и (n +1)/ 2 разрезов r1r2 , …, rn−2rn−1 , rn∞, если n нечетно. Взяв два экземпляра z -сферы с такими разрезами, склеиваем их по соответствующим разрезам. Построения, аналогичные изображенным на рисунке
n |
|
|
n − 2 |
|
n +1 |
−1 |
= |
n −1 |
|
||
140, дадут сферу с |
−1 |
= |
|
или с |
|
|
|
|
ручками. Это и есть |
||
2 |
2 |
|
2 |
|
|||||||
2 |
|
|
|
|
|
|
|
|
|||
риманова поверхность функции (15.15). Число ручек p (род поверхности) связано с числом V точек ветвления римановой поверхности равенством V = 2(p +1).
Таким образом, многозначная алгебраическая функция, определяемая уравнением (15.9), имеет риманову поверхность, топологически эквивалентную сфере с ручками. Это утверждение справедливо для любой многозначной алгебраической функции.
Изучение алгебраических аналитических функций w(z), удовлетворяющих уравнению f (z, w)= 0 с неалгебраической аналитической функцией f , в z -
плоскости также приводит к римановым поверхностям, на которых аналитические функции однозначны.
15.5 Вопросы для самоконтроля
1Какие преобразования сферы называются гомеоморфизмами?
2Какие фигуры называются гомеоморфными?
3Какие свойства фигур называются топологическими?
4Определите направление комбинаторной (алгебраической) топологии?
5Изучением каких вопросов занимается «общая топология»?
6Какая кривая называется простой замкнутой?
7Сформулируйте понятие n -мерного многообразия.
8Какое n -мерное многообразие называют топологическим (гладким)?
9Какое пространство называют расслоенным?
10Дайте определение симплекса (вершины симплекса).
11Сформулируйте определение размерности симплекса.
12Что означает пересечение симплексов?
13Сформулируйте определение метрического пространства (обозначение).
14Сформулируйте определение метрики пространства X .
15Какое метрическое пространство называется дискретным?
370
16 Сформулируйте определение сходимости последовательности {xn } к
точке a .
17 Дайте определение непрерывного отображения метрического пространства (X , ρ1 ) в метрическое пространство (Y , ρ2 ).
18 Дайте |
определение |
непрерывного |
отображения |
метрических |
пространств на языке ε , δ . |
|
|
|
|
19 Какое |
отображение метрических пространств f : X →Y |
называется |
||
гомеоморфизмом?
20 Какое отображение f : X →Y называют вложением пространства X в
Y ?
21Какое множество называется проективной плоскостью?
22Сформулируйте определение окрестности точки x0 .
23Какое множество X называют топологическим пространством?
24Какие топологические пространства называются топологически эквивалентными?
25Что называется тором с дырой?
26Какое разбиение пространства называется триангуляцией?
27Какие пространства называются двумерными многообразиями?
28Дайте определение замкнутых поверхностей.
29Какие многообразия называются замкнутыми поверхностями (незамкнутыми)?
30Какое топологическое пространство называется топологическим многоугольником (вершины, ребра топологического многоугольника)?
31какая аналитическая функция w = w(z) называется алгебраической
функцией?
32Сформулируйте понятие римановой поверхности?
33Как можно построить риманову поверхность?
34Объясните какое отображение S 2 z =w2 →S 2 называется двулистным (разветвленным) накрытием сферы S 2 с точками ветвления z = 0 и z = ∞.
35Приведите пример двулистного накрытия сферы S 2 с двумя точками ветвления z = r1 и z = r2 .
371
