8.1 Аффинная и прямоугольная декартовы системы координат. Простейшие задачи
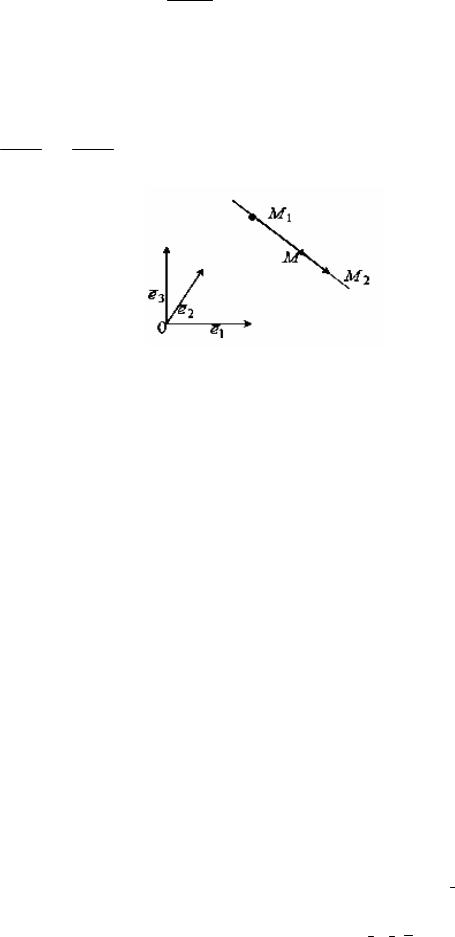
Пусть в пространстве даны точка O и базис {e1 , e2 , е3 }.
Совокупность точки O и базиса {e1 , e2 , е3 } называется аффинной
системой координат в пространстве (или аффинным репером), и обозначается R (O; e1 , e2 , е3 ) или Oxyz (рисунок 72).
Точка O называется началом координат. Ось, проходящая через точку O и имеющая направление вектора e1 , называется осью Ox или осью абсцисс.
Рисунок 72
Ось, проходящая через точку O и имеющая направление вектора e2 , называется осью Oy или осью ординат. Ось, проходящая через точку O и имеющая направление вектора e3 , называется осью Oz или осью аппликат.
Выделяют также три плоскости, называемые координатными. Каждая из них содержит по две координатные оси. Обозначаются плоскости следующим образом: Oxy , Oyz,Oxz.
Пусть на плоскости задан аффинный репер R (O;
e1 , e2 , e3 ) и любая точка
M . Рассмотрим
- радиус-вектор точки M и пусть
= xe1 + ye2 + ze3 .
OM
OM
Координатами
точки
M
относительно
аффинного
репера
R (O; e1 , e2 , e3 ) называются координаты радиус-вектора этой точки относительно
базиса {e1 , e2 , e3 }. Пишут: M (x, y, z)R .
Так же как и на плоскости, аффинная система координат в пространстве
позволяет решать ряд простейших задач. Рассмотрим три из них.
1 Нахождение координат вектора, заданного координатами начала и
Точка M , принадлежащая прямой M1M 2 , делит отрезок M1M 2 в отношении λ (λ ≠ −1) (рисунок 73), если выполняется векторное равенство:
M1M = λMM2 .
Рисунок 73
Если λ > 0 , то
↑↑
и говорят, что точка M делит отрезок M1M 2
M1M
MM2
внутренним образом в отношении λ .
Если λ < 0 , то
↑↓
и точка M лежит вне отрезка M1M 2 , но на
M1M
MM2
прямой M1M 2 ,
тогда говорят,
что
точка M делит отрезок
M1M 2 внешним
образом в отношении λ .
репера R (O; e1 , e2 , е3 )
даны
точки
Пусть
относительно аффинного
M1 (x1 , y1 , z1 )R ,
M 2 (x2 ,
y2 , z2 )R . Найдем координаты точки M ,
которая делит
отрезок M1M 2 в отношении λ . Обозначим M (x, y, z)R , тогда формулы для
нахождения координат точки, делящей отрезок в отношении λ имеют вид
x =
x1 + λx2
; y =
y1 + λy2
; z =
z1 + λz2
(8.3)
1 + λ
1 + λ
1 + λ
В
частности, при λ =1
(то
есть
точка M - середина
отрезка
M1M 2 ),
имеем:
x
+ x
2
x =
1
2
y
+ y
2
y
=
1
- формулы для нахождения координат середины отрезка.
2
z + z
2
z
=
1
2
Совокупность точки O и ортонормированного базиса {i
;
}называется
, k
j
прямоугольной декартовой системой координат в пространстве (или ортонормированным репером). Обозначается R (O; i , j, k ) (рисунок 74).
191
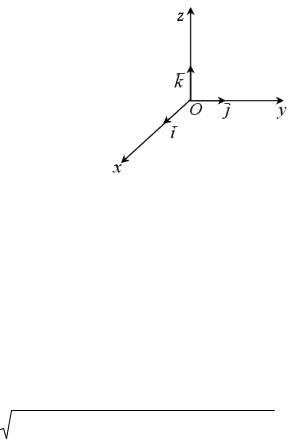
Рисунок 74
Очевидно, что прямоугольная декартова система координат является частным случаем аффинной системы координат, поэтому рассмотренные выше определения и простейшие задачи справедливы и в прямоугольной декартовой системе координат.
Нахождение расстояния между двумя точками.
Пусть
относительно
R (O;
)
заданы
точки
,
, k
i
j
M1 (x1 , y1 , z1 )R ,
M 2 (x2 ,
y2 , z2 )R . Найдем расстояние от точки M1 до точки M 2 .
ρ(M
1
; M
2
)=
(x
2
− x )2 + (y
2
− y )2 + (z
2
− z )2 .
(8.4)
1
1
1
8.2 Уравнение поверхности и линии в пространстве
Поверхностью в пространстве называется геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О есть геометрическое место всех точек пространства, находящихся от точки О на расстоянии R.
Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел х,у,z — их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности.
Уравнением данной поверхности в прямоугольной системе координат Оyz называется такое уравнение F(x, y, z) = 0 , которому удовлетворяют
координаты каждой точки лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х,у,z в уравнении поверхности называются текущими координатами точек поверхности.
Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка M1 (x1, y1, z1 ) на данной поверхности достаточно подставить
координаты точки M1 в уравнение поверхности вместо переменных: если эти
координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют — не лежит.
192
Уравнение сферы
Найдем уравнение сферы радиуса R с центром в точке О(x0 , y0 , z0 ) .
Согласно определению сферы расстояние любой ее точки
M (x, y, z) от центра
О1 (x0 , y0 , z0 ) равно радиусу R, т. е. О1M = R . Но
О1M =
где
O1M
О1M = (x − x0 , y − y0 , z − z0 ) .
Следовательно,
(x − x0 )2 +( y − y0 )2 +(z − z0 )2 = R
или
( x − x0 )2 + ( y − y0 )2 + (z − z0 )2 = R2 .
(8.5)
Это и есть искомое уравнение сферы. Ему удовлетворяют координаты
любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.
Если центр сферы О1 совпадает с началом координат, то уравнение сферы
принимает вид
x2 + y2 + z 2 = R2 .
Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:
1 Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.
2 Дано уравнение F(x, y, z) = 0 . Исследовать форму поверхности, определяемой этим уравнением.
Уравнения линии в пространстве
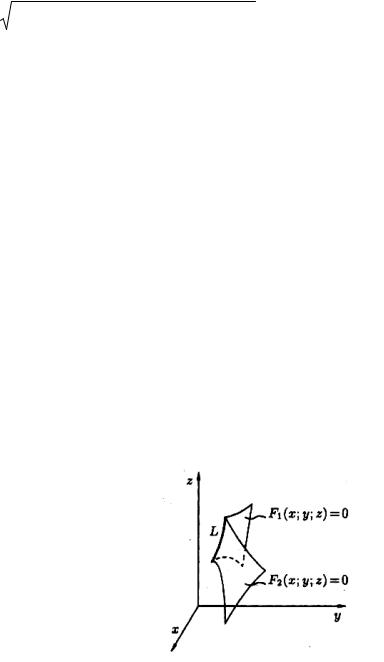
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (рисунок 75) или как геометрическое место точек, общих двум поверхностям.
Рисунок 75
Если F1 (x, y, z) = 0 и F2 (x, y, z) = 0 - уравнение двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе
193
двух уравнений с тремя неизвестными:
F
(x, y, z) = 0,
(8.6)
1
F2 (x, y, z) = 0.
Уравнения системы (8.6) называются уравнениями линий в пространстве.
y = 0,
Например, есть уравнение оси Ох.
z = 0.
Линию в пространстве можно рассматривать как траекторию движения
точки (рисунок 76). В этом случае ее задают векторным уравнением
r = r (t)
(8.7)
Рисунок 76
или параметрическими уравнениями
x = x(t),
(8.8)
y = y(t),
z = z(t).
проекций вектора (8.7) на оси координат.
8.3 Уравнения плоскости в пространстве
Простейшей поверхностью в пространстве является плоскость. Плоскость в пространстве Oxyz можно задать различными способами. Каждому из них соответствует определённый вид ее уравнения.
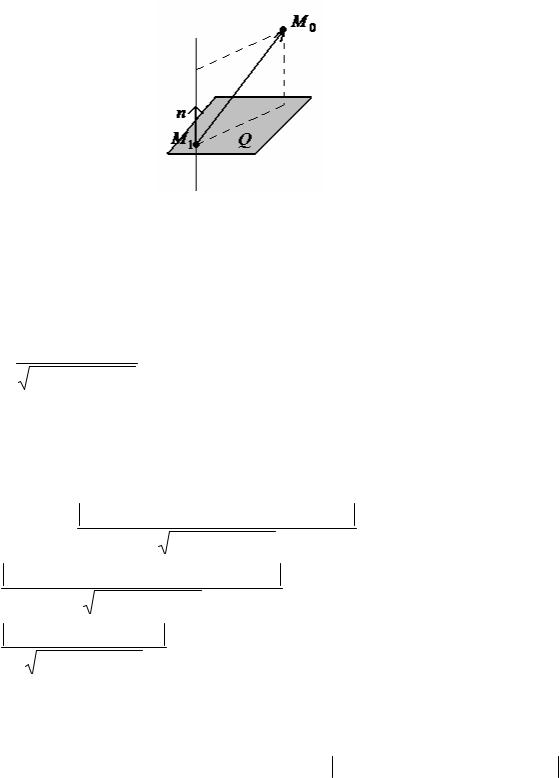
1 Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
Пусть в пространстве Oxyz плоскость Q задана точкой М0 (x0 , y0 , z0 ) и вектором n ={A,B,C}, перпендикулярным этой плоскости (рисунок 77).
Выведем уравнение плоскости Q. Возьмем на ней произвольную точку M (x, y, z) и составим вектор М0 M ={x − x0 , y − y0 , z − z0 }.
194
Рисунок 77
При любом расположении точки М на плоскости Q векторы n и М0 M взаимно перпендикулярны, поэтому их скалярное произведение равно нулю:
n М0 M = 0 , т. е.
A( x − x0 ) + B( y − y0 ) +C( z − z0 ) = 0 .
(8.9)
Координаты любой точки плоскости Q удовлетворяют уравнению (8.9), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют.
Уравнение (8.9) называется уравнением плоскости, проходящей через данную точку М0 (x0 , y0 , z0 ) перпендикулярно вектору n ={A,B,C}. Оно первой
степени относительно текущих координат x, y, z. Вектор n ={A,B,C} называется
нормальным вектором плоскости.
Придавая коэффициентам А, В и С уравнения (8.9) различные значения, можно получить уравнение любой плоскости, проходящей через точку М0 (x0 , y0 , z0 ) . Совокупность плоскостей, проходящих через данную точку,
называется связкой плоскостей.
2 Общее уравнение плоскости
Раскрыв скобки в уравнении (8.9)
Ax + By +Cz + (Ax0 + By0 +Cz0 )=0
и введя обозначения
Ax0 + By0 +Cz0 = D, получим общее уравнение
первой
степени с тремя переменными x, y, z :
Ax + B y + C z + D = 0 .
(8.10)
Полагая, что по крайней мере один из коэффициентов А, В или С не равен
нулю, например В ≠ 0 , перепишем уравнение (8.10) в виде
D
A(x − 0) + B y +
+ C( z − 0) = 0.
(8.11)
B
Сравнивая уравнение (8.11) с уравнением (8.9), видим, что уравнения (8.10), а, следовательно, и (8.11) являются уравнением плоскости с нормальным
вектором n ={A,B,C}, проходящей через точку М1 0,− DB ,0 .
Ax + By + Cz + D = 0
195
Уравнение (8.10) называется общим уравнением плоскости.
Частные случаи общего уравнения плоскости:
1 Если D = 0, то оно принимает вид Ax + B y + C z = 0 . Этому уравнению
удовлетворяет точка О(0, 0, 0), Следовательно, в том случае плоскость проходит через начало координат.
2 Если C = 0 , то имеем уравнение Ax + B y + D = 0 . Нормальный вектор n = (A, B,0) перпендикулярен оси Oz. Следовательно, плоскость параллельна оси Oz; если B = 0 -параллельна оси Оу, A = 0 — параллельна оси Ох.
3 Если C = D = 0, то плоскость проходит через О(0, 0, 0) параллельно оси Oz, т. е. плоскость Ax + B y = 0 проходит через ось Oz. Аналогично, уравнениям
B y + C z = 0 и Ax + C z = 0 отвечают плоскости, проходящие соответственно
через оси Ох и Оу.
4
Если
A = B = 0, то уравнение (8.10)
принимает вид C z + D = 0 , т. е.
z = −
D
.
Плоскость параллельна
плоскости
Оху.
Аналогично, уравнениям
C
Ax + D = 0 и
B y + D = 0 отвечают
плоскости, соответственно параллельные
плоскостям Oyz и Оxz.
5
Если
A = B = D = 0 , то уравнение (8.10) примет вид C z = 0, т. е, z = 0 .
Это уравнение плоскости Оху. Аналогично: y = 0 -
уравнение плоскости Oxz;
x = 0 — уравнение плоскости Оуz.
3 Уравнение плоскости, проходящей через три данные точки
Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M1 (x1 , y1, z1 ), M 2 (x2 , y2 , z2 ), М3 (x3 , y3 , z3 ) , не лежащие на одной
прямой.
Возьмем на плоскости произвольную точку M (x, y, z) и составим векторы
={x − x1 , y − y1 , z − z1},
={x2 − x1 , y2 − y1 ,z2 − z1}
М1M
М1M 2
={x3 − x1 , y3 − y1 , z3 − z1}.
М1M 3
Эти векторы лежат на плоскости Q, следовательно, они компланарны. Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем
М1M М1М2 М1М3 = 0,
т.е.
x − x1
y − y1
z − z1
x2 − x1
y2 − y1
z2 − z1
= 0.
(8.12)
x3 − x1
y3 − y1
z3 − z1
Уравнение (8.12) есть уравнение плоскости, проходящей через три
196
данные точки.
Например, составим уравнение плоскости, проходящей через три точки
M1 (1,−4,9), M 2 (− 2,−5,7), М3 (3,−6,8) .
Подставив координаты точек M1 , M 2 и M 3 в формулу (8.12) получаем:
x −1
y + 4 z − 9
x −1 y +4 z −9
− 2 −1 − 5 + 4
7 − 9
= 0,
−3
−1
−2
= 0,
3 −1 − 6 + 4
8 − 9
2
−2
−1
(x −1) −1
−2 −( y + 4)
−3 −2 +(z −9)
−3 −1
= 0
,
−2
−1
2 −1
2 −2
3x + 7 y −8z + 97 = 0
- уравнение искомой плоскости.
4 Уравнение плоскости в отрезках
Пусть плоскость отсекает на осях Ох, Оу и 0z соответственно отрезки а, b и с, т. е. проходит через три точки А(а,0,0), В(0,b,0) и С(0,0,с) (рисунок 78).
Рисунок 78
Подставляя координаты этих точек в уравнение (8.12), получаем
x − a
y
z
− a
b
0
= 0.
− a
0
c
Раскрыв
определитель, имеем
bcx − abc + abz + acy = 0 ,
т. е.
bcx + acy + abz = abc или
x
+
y
+
z
=1.
(8.13)
a
b
c
Уравнение (8.13) называется уравнением плоскости в отрезках на осях.
5 Нормальное уравнение плоскости
Положение плоскости Q вполне определяется заданием единичного вектора е , имеющего направление перпендикуляра ОК, опущенного на плоскость
197
из начала координат, и длиной р этого перпендикуляра (рисунок 79)
Рисунок 79
Пусть ОК = р, а α, β, γ
— углы, образованные единичным вектором е с
осями Ох, Оу, Оz. Тогда
е ={cosα,cosβ,cosγ}. Выберем на плоскости
произвольную точку M (x, y, z)
и соединим ее с началом координат. Получим
вектор r = OM ={x, y,z}.
При любом положении точки М на плоскости Q проекция радиус-вектора
r на направление вектора е всегда равна р: преr = p , т.е. r e = p или
r e − p = 0.
(8.14)
Уравнение (8.14) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов r и e , уравнение (8.14) перепишем
в виде
x cosα + y cos β + z cos γ − p = 0 .
(8.15)
Уравнение (8.15) называется нормальным уравнением плоскости в координатной форме.
Отметим, что общее уравнение плоскости (8.10) можно привести к нормальному уравнению (8.15) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (8.10) на нормирующий
множитель λ =
1
, где знак берется противоположным знаку
А2 + В2 + С2
±
свободного члена D общего уравнения плоскости.
8.4 Плоскость. Основные задачи
1 Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей
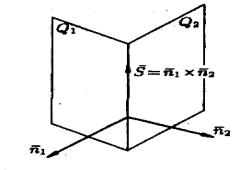
Пусть заданы две плоскости Q1 и Q2 :
Q1: A1 x + B1 y +C1 z + D1 = 0,
198
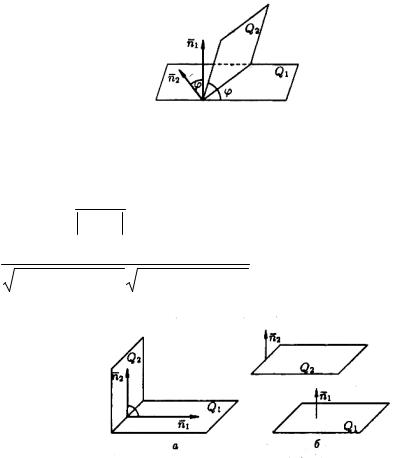
Q2 : A2 x + B2 y +C2 z + D2 = 0 .
Под углом между плоскостями Q1 и Q2 понимается один из двугранных
углов, образованных этими плоскостями.
На основании рисунка 80 заключаем, что угол ϕ между нормальными векторами n1 ={A1 ,B1 ,C1} и n2 = {A2 ,B2 ,C2} плоскостей Q1 и Q2 равен одному из этих углов.
Рисунок 80
Поэтому cosϕ = n1 n2 или n1 n2
cosϕ =
A1 A2
+ B1B2
+ C1C2
.
(8.16)
A2 + B2 + C 2 A2 + B2 + C 2
Для нахождения острого угла следует взять модуль правой части.
Рисунок 81
Если плоскости Q1 и Q2 перпендикулярны (рисунок 81, а), то их нормальные векторы тоже перпендикулярны, т. е. n1 n2 (и наоборот). Но тогда
n1 n2 = 0 , т. е. A1A2 + B1B2 +C1C2 =0 . Полученное равенство есть условие перпендикулярности двух плоскостей Q1 и Q2 .
Если плоскости Q1 и Q2 параллельны (рисунок 81. б), то будут
коллинеарны и их нормальные векторы n1, n2
(и наоборот). Из условия
коллинеарности векторов получаем, что
А1
=
В1
=
С1
.
(8.17)
А
В
С
2
2
2
Это и есть условие параллельности плоскостей Q1 и Q2 .
199
2 Расстояние от точки до плоскости
Рассмотрим в пространстве некоторую плоскость Q и произвольную точкуМ0 (x0 , y0 , z0 ) . Выберем для плоскости единичный нормальный вектор n с
началом в некоторой точке М1(x1, y1, z1) Q , и пусть
ρ(М0 ,Q) - расстояние от
точки М0 до плоскости Q . Тогда (рисунок 82)
ρ(М0 ,Q) =
прn
=
n
,
(8.18)
M1M 0
M1M 0
так как
n
=1.
Рисунок 82
Если плоскость Q задана в прямоугольной системе координат своим
уравнением Ax + B y + C z + D = 0 , то ее нормальным вектором является вектор с координатами {A, B,C} и в качестве единичного нормального вектора можно выбрать
n =
{A, B,C} .
A2 + B2 + C 2
Так как точка M1 Q , то можно найти координаты вектора
:
M1M 0
= {x0 − x1 , y0 − y1 , z0 − z1}.
M1M 0
Записывая
скалярное
произведение
n
в координатной форме
и
M1M 0
преобразуя (8.18), получаем
ρ(М0
,Q) = A(x0 − x1) + B( y0 − y1) + C(z0 − z1) =
A2 + B2 + C 2
= Ax0 + By0 + Cz0 − ( Ax1 + By1 + Cz1)
=
A2 + B2 + C 2
=
Ax0
+ By0 + Cz0 + D
,
A2 + B2 + C 2
поскольку Ax1 + By1 + Cz1 = −D .
Q
задана
уравнением
Отметим,
что
если
плоскость
x cosα + y cos β + z cos γ − p = 0 , то
расстояние
от
точки М0 (x0 , y0 , z0 )
до
плоскости Q может быть найдено по формуле d = x cosα + y cos β + z cos γ − p .
200
8.5 Уравнения прямой в пространстве
1 Векторное уравнение прямой
Положение прямой в пространстве вполне определено, если задать какую-
либо точку М0 на прямой и вектор s , параллельный этой прямой. Вектор s
называется направляющим вектором прямой. Пусть прямая L задана точкой
М0 (x0 , y0 , z0 )
и направляющим вектором s ={m,n, p}. Возьмем на прямой L
произвольную
точку М(x, y, z) . Обозначим радиус-векторы
точек М и М0
соответственно через
r
и
r0 . Очевидно, что три вектора
r
r0
и
связаны
,
M 0 M
соотношением
=
r0 +
(8.19)
r
M 0 M
Вектор M 0 M , лежащий на прямой L, параллелен направляющему вектору
s , поэтому M 0 M = ts , где t — скалярный множитель, называемый параметром,
может принимать различные значения в зависимости от положения точки М на прямой (рисунок 83)
Рисунок 83
Уравнение (8.19) можно записать в виде
r
=
r0 +ts
(8.20)
Полученное уравнение называется векторным уравнением прямой.
есть (8.21) napaметрические уравнения прямой в пространстве.
201
3 Канонические уравнения прямой
Пусть
={m,n, p} — направляющий вектор прямой L и
М0 (x0 , y0 , z0 )
s
точка, лежащая на этой прямой. Вектор
, соединяющий точку М0 с
M 0 M
произвольной точкой М(x, y, z)
прямой L, параллелен вектору s . А значит, эти
векторы
коллинеарны.
Поэтому
координаты
вектора
={x − x0 , y − y0 , z − z0 } и вектора s ={m,n, p} пропорциональны:
М0 M
x − x0
=
y − y0
=
z − z0
.
(8.22)
m
n
p
Уравнения (8.22) называются каноническими уравнениями прямой в пространстве.
Замечания: 1) Уравнения (8.22) можно было бы получить сразу из параметрических уравнении прямой (8.21), исключив параметр t. Из уравнений
(8.21) находим
x − x0
=
y − y0
=
z − z0
= t.
m
n
p
2) Обращение в нуль одного из знаменателей уравнений (8.22) означает
обращение в нуль соответствующего числителя.
Например, уравнения
x
−1
=
y
+1
=
z −
3
задают прямую, проходящую
2
0
4
через точку М0 (1,−1,3) перпендикулярно оси Оу (проекция вектора s
на ось Oу
равна нулю). Но это означает, что прямая лежит в плоскости
у = −1,
и поэтому
для всех точек прямой будет у +1 = 0 .
4 Уравнение прямой в пространстве, проходящей через две точки
Пусть прямая L проходит через точки
s
M1 (x1 , y1 , z1 ),
M 2 (x2 ,
y2 , z2 ). В
качестве
направляющего
вектора
можно
взять
вектор
={x2 − x1 , y2 − y1 , z2 − z1}, т.е. s =
(рисунок 84).
М1M 2
М1М2
Рисунок 84
Следовательно,
m = x2 − x1
, n = y2 − y1, p = z2 − z1 . Поскольку прямая
проходит через точку
M1 (x1, y1, z1 ), то, согласно уравнениям (8.22), уравнения
прямой L имеют вид
202
x − x1
=
y − y1
=
z − z1
.
(8.23)
x
2
− x
y
2
− y
z
2
− z
1
1
1
Уравнения (8.23) называются уравнениями прямой, проходящей через две данные точки.
5 Общие уравнения прямой
Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей. Рассмотрим систему уравнений
A x + B y + C z + D = 0,
(8.24)
1
1
1
1
A2 x + B2 y + C2 z + D2 = 0.
Каждое из уравнений этой системы определяет плоскость. Если плоскости
не параллельны
(координаты векторов n1 ={A1 ,B1 ,C1
}
и
n2 ={A2 ,B2 ,C2 } не
пропорциональны), то система (8.24) определяет прямую L как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы (рисунок 85).
Рисунок 85
Уравнения (8.24), т.е.
A1 x + B1 y + C1 z + D1 = 0,A2 x + B2 y + C2 z + D2 = 0.
называют общими ypaвнениями прямой.От общих уравнений (8.24) можно перейти к каноническим уравнениям (8.22). Координаты точки М0 (x0 , y0 , z0 ) на
прямой L получаем из системы уравнений (8.24), придав одной из координат произвольное значение (например, z = 0 ).
Так как прямая L перпендикулярна векторам n1, n2 , то за направляющий
вектор s прямой L можно принять векторное произведение [n1, n2
]:
k
s = [n1 , n2 ]=
i
j
A1
B1
C1
.
A2
B2
C2
Замечание: Канонические уравнения прямой легко получить, взяв две какие-либо точки на ней и применив уравнения (8.23).
203
8.6 Прямая линия в пространстве. Основные задачи
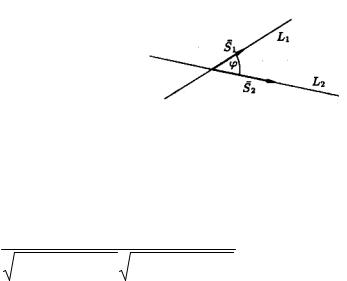
1 Угол между прямыми. Условия параллельности и перпендикулярности прямых.
Пусть прямые L1 и L2 заданы уравнениями
L
:
x − x1
=
y − y1
=
z − z1
,
1
m1
n1
p1
L
:
x − x2
=
y − y2
=
z − z2
.
2
m2
n2
p2
Под углом между этими прямыми понимают угол между
направляющими векторами s1 ={m1 ,n1 , p1
} и s2 ={m2 ,n2 , p2
}(рисунок 86).
Рисунок 86
Поэтому, по известной формуле для косинуса угла между векторами, получаем
cosϕ =
s1 s2
или
s
s
2
1
cosϕ =
m1m2 +n1n2 + p1 p2
.
(8.25)
+n2
+ p2
m2 +n2
m2
+ p2
1
1
1
2
2
2
Для нахождения острого угла между прямыми L1 и L2 числитель правой
Если прямые L1 и L2 параллельны, то параллельны их направляющие векторы s1 и s2 . Следовательно, координаты этих векторов пропорциональны, т.е.
m1
=
n1
=
p1
- условие параллельности прямых.
m
2
n
p
2
2
2 Условие, при котором две прямые лежат в одной плоскости.
Пусть прямые L1 и L2 заданы каноническими уравнениями
x − x1
=
y − y1
=
z − z1
и
x − x2
=
y − y2
=
z − z2
n
p
m
m
2
n
2
p
2
1
1
1
204
Их направляющие векторы соответственно
s1 ={m1 ,n1 , p1} и
s2 ={m2 ,n2 , p2 }(рисунок 87).
Рисунок 87
Прямая L1 проходит через точку M1 (x1, y1, z1 ) , радиус-вектор которой обозначим через r1 ; прямая L2 проходит через точку M 2 (x2 , y2 , z2 ) , радиусвектор которой обозначим через r2 . Тогда
r2 − r1 = M1M 2 ={x2 − x1 , y2 − y1 , z2 − z1}.
Прямые L1 и L2 лежат в одной плоскости, если векторы s1 , s2 , M1M 2 компланарны. Условием компланарности векторов является равенство нулю их смешанного произведения: s1 s2 M1M 2 = 0, т.е.
x2 − x1
y2 − y1 z2 − z1
m1
n1
p1
= 0.
m2
n2
p2
условия прямые L1 и L2 лежат в одной
При выполнении
этого
плоскости, то есть либо пересекаются, если s2 ≠ λs1 , либо параллельны, если s2 = λs1.
8.7 Прямая и плоскость в пространстве. Основные задачи
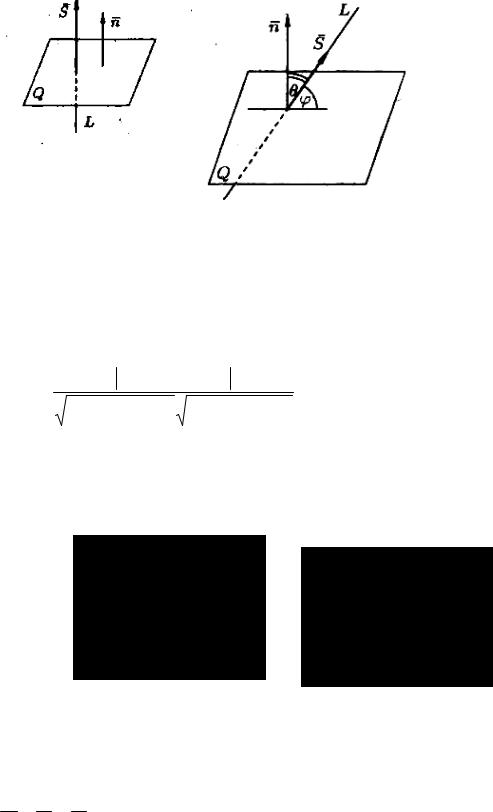
1 Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
Пусть
плоскость Q задана уравнением Ax + B y + C z + D = 0 , прямая L
уравнениями
x − x0
=
y − y0
=
z − z0
.
m
n
p
Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Обозначим через ϕ - угол между плоскостью Q и прямой L, а через θ -угол, между векторами n ={A,B,C},s ={m,n, p} (рисунок 88).
205
Рисунок 88
Тогда cosθ =
n
s
. Найдем синус угла ϕ , считая ϕ ≤
π
:
n
s
2
π
= cosθ . Так как sin ϕ ≥ 0 , получаем
sin ϕ = sin
−θ
2
sinϕ =
Am + Bn + Cp
A2 + B2 + C 2 m2 + n2 + p2 .
(8.26)
Если прямая L параллельна плоскости Q, то векторы n, s перпендикулярны (рисунок 89), а потому n s = 0 , т. е.
Am + Bn +Cp = 0
является условием параллельности прямой и плоскости.
Рисунок 89 Рисунок 90
Если прямая L перпендикулярна плоскости Q, то векторы n, s
параллельны (рисунок 90). Поэтому равенства mA = Bn = Cp
являются условиями перпендикулярности прямой и плоскости.
206
2 Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости
Для того, чтобы найти точку пересечения прямой
x − x0
=
y − y0
=
z − z0
(8.27)
m
n
p
с плоскостью
Ax + B y + C z + D = 0 ,
(8.28)
надо решить систему уравнений (8.27) и (8.28). Проще всего это сделать, записав уравнения прямой (8.27) в параметрическом виде:
x = x0 +mt,
= y0
+nt,
y
= z0
+ pt.
z
Подставляя выражения для x, y, z в уравнение плоскости (8.28), получаем
уравнение A(x0 +mt) + B( y0 +nt) +C(z0 + pt) + D = 0 или
t(Am + Bn + Cp) + (Ax0 + By0 + Cz0 + D) = 0 .
(8.29)
Если прямая L не параллельна плоскости, т. е. если Am + Bn + Cp ≠ 0 , то из
равенства (8.29) находим значение t:
t = − Ax0 + By0 + Cz0 + D . Am + Bn + Cp
Подставляя найденное значение t в параметрические уравнения прямой, находим координаты точки пересечения прямой с плоскостью.
Рассмотрим теперь случай, когда прямая L параллельна плоскости Q, т.е.
если Am + Bn +Cp = 0 :
а) если F = Ax0 + By0 + Cz0 + D ≠ 0 , то прямая L параллельна плоскости
и пересекать ее не будет (уравнение (8.29) решения не имеет, так как имеет вид
0 t + F = 0, F ≠ 0 );
б) если Ax0 + By0 + Cz0 + D = 0 , то уравнение (8.29) имеет вид
0 t + 0 = 0 ; ему удовлетворяет любое значение t, любая точка прямой является точкой пересечения прямой и плоскости. Заключаем: прямая лежит в плоскости. Таким образом, одновременное выполнение равенств
Am + Bn + Cp = 0,
Ax0 + By0 + Cz0 + D = 0.
является условием принадлежности прямой плоскости.
3 Расстояние от точки до прямой
Расстояние от точки М1 (x1, y1, z1 ) до прямой L, заданной каноническими
уравнениями
x − x0
=
y − y0
=
z − z0
, может быть вычислено при помощи
m
n
p
207
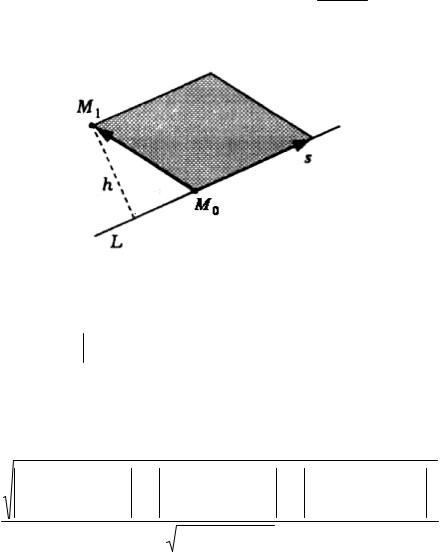
векторного произведения. Из канонического уравнения прямой можем найти точку М0 (x0 , y0 , z0 ) принадлежащую этой прямой и ее направляющий вектор
s ={m,n, p}. Построим параллелограмм на векторах s и M 0 M1 . Тогда расстояние от точки M1 до прямой L будет равно высоте h параллелограмма (рисунок 91).
Рисунок 91
Значит, расстояние вычисляется по формуле
[
, s]
ρ(М1
, L) =
M 0M1
(8.30)
,
s
где числитель представляет собой площадь этого параллелограмма. Используя формулы вычисления длины вектора и векторного произведения векторов через их координаты, получаем
y − y
0
z −z
2
x − x
z −z
0
2
x − x
0
y − y
2
1
1
0 +
1
0 1
+
1
1
0
ρ(М1, L) =
n
p
m
p
m
n
(8.31)
m2 +n2 + p2
- формула расстояния от точки до прямой.
4 Расстояние между прямыми
Если прямые пересекаются, то очевидно, что расстояние между ними равно нулю. Поэтому о расстоянии имеет смысл говорить если прямые параллельны или скрещиваются. Чтобы найти расстояние между параллельными прямыми, достаточно вычислить расстояние от произвольной точки, например, второй прямой до первой прямой, т.е. можно воспользоваться формулой (8.31)
Пусть две прямые заданы каноническими уравнениями
L :
x − x1
=
y − y1
=
z − z1
, L
2
:
x − x2
=
y − y2
=
z − z2
.
1
m1
n1
p1
m2
n2
p2
Таким образом расстояние между ними вычисляется по формуле
208
y − y z
2
−z
2
+
x −x z
2
−z
2
+
x −x y − y
2
2 1
1
2
1
1
2 1
2 1
n
p
m
p
m
n
ρ(L1, L2 ) =
1
1
1
1
1
1
.
(8.32)
m 2
+n 2
+ p
2
1
1
1
Следующую формулу примем без доказательства.
Расстояние между скрещивающимися прямыми, заданными уравнениями
L :
x − x1
=
y − y1
=
z − z1
, L
2
:
x − x2
=
y − y2
=
z − z2
.
1
m1
n1
p1
m2
n2
p2
m1
n1
p1
m2
n2
p2
ρ(L1 , L2 ) =
x2 − x1
y2 − y1
z2 − z1
.
(8.33)
n
p
2
m
p 2
m
n 2
+
1
1
+
1
1
1
1
n2
p2
m2
p2
m2
n2
5 Расстояние между прямой и плоскостью
Если прямая L и плоскость Q пересекаются,
то расстояние между ними
равно нулю. Если же они параллельны, то расстояние от прямой до плоскости есть расстояние от любой точки прямой до данной плоскости.
Пусть плоскость
задана общим уравнением Q : Ax + B y + C z + D = 0 , а
прямая каноническими
уравнениями
L :
x − x0
=
y − y0
=
z − z0
. Канонические
m
n
p
уравнения прямой позволяют найти координаты точки М0 (x0 , y0 , z0 ) , лежащей на ней. Поэтому расстояние между прямой L и параллельной ей плоскостью Q
равно
ρ(L,Q) = ρ(М0 ,Q) =
Ax0
+ By0
+ Cz0
+ D
.
(8.34)
A2 + B2 + C 2
8.8 Уравнение цилиндрической поверхности с образующей, параллельной координатной оси. Цилиндры второго порядка
Цилиндрической поверхностью называется поверхность, описываемая прямой (образующей), движущейся вдоль некоторой линии (направляющей) и остающейся параллельной исходному направлению (рисунок 92)
209
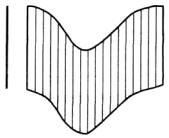
Рисунок 92
Рассмотрим уравнение
F(x, y) = 0 ,
(8.35)
особенность которого состоит в том, что оно не содержит переменной z. Покажем, что если это уравнение определяет некоторую поверхность, то
она является цилиндрической поверхностью с образующей, параллельной оси Oz. Действительно, если х0 , у0 - значения переменных х и у, удовлетворяющих
уравнению (8.35), т.е. М0 (х0 , у0 , z0 ) принадлежит поверхности, определяемой уравнением, то ей будет принадлежать и точка М0 (х0 , у0 , z), так как z в
уравнении (8.35) не входит. Следовательно, поверхности целиком принадлежит прямая, проходящая через точки М0 , М , а эта прямая параллельна оси Оz. Итак,
поверхность, определяемая уравнением F ( x, y) = 0 , является цилиндрической
поверхностью с образующей, параллельной оси Оz.
Отметим, что в плоскости Оху уравнение (8.35) определяет линию (направляющую), которая в пространстве задается уже двумя уравнениями
F(x, y) = 0,
(8.36)
z = 0.
(уравнения (8.36) задают эту линию как пересечение цилиндрической поверхности (8.35) и координатной плоскости Оху).
Цилиндром второго порядка называется цилиндрическая поверхность, направляющей которой является эллипс (окружность), гипербола или парабола.
К цилиндрам второго порядка относятся эллиптический цилиндр (рисунок 93), определяемый уравнением
x2
+
y2
=1;
(8.38)
a2
b2
210
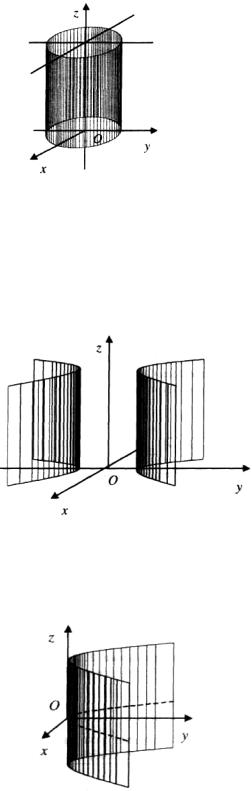
Рисунок 93
В некоторой системе декартовых прямоугольных координат; гиперболический цилиндр (рисунок 94), определяется уравнением
−
x2
+
y2
=1.
(8.39)
a2
b2
Рисунок 94
Параболический цилиндр (рисунок 95), определяется уравнением
х2 =2ру.
(8.40)
или уравнением
Рисунок 95
у2 =2рх.
(8.41)
Замечание 1 Если уравнение
F(x, z) = 0
211
определяет некоторую поверхность, то ею является цилиндрическая поверхность с образующей, параллельной оси Оу.
Замечание 2. Если уравнение
F( y, z) = 0
определяет некоторую поверхность, то ею является цилиндрическая поверхность с образующей, параллельной оси Ох.
8.9 Уравнение поверхности вращения
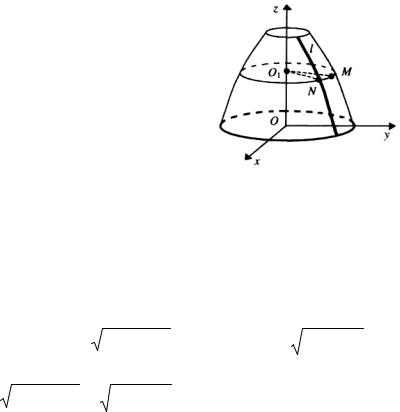
Рассмотрим поверхность, полученную вращением линии l, вокруг оси Оz заданной уравнениями
x =ϕ1 (z), y =ϕ2 (z),
(8.42)
Пусть М – произвольная точка этой поверхности, X, Y, Z - ее текущие координаты. Через точку М проведем плоскость, перпендикулярную оси Оz; эта плоскость (ее уравнение z=Z) пересечет поверхность по некоторой окружности с центром в точке О1 (0,0, z) на оси Оz (рисунок 96).
Рисунок 96
Обозначим буквой N точку пересечения указанной окружности и линии l, а буквами х, у, z – ее координаты.
Поскольку длины отрезков О1М и О1N равны между собой (как радиусы одной и той же окружности), т.е. ρ(O1, M ) = ρ(O1, N) и
ρ(O , M ) = X 2
+Y 2 ,
ρ(O , N) = x2 + y 2
,
1
1
то
X 2 +Y 2 =
x2 + y 2 ,
X 2 +Y 2 = x2 + y 2 .
(8.43)
Для координат
точки
N ( x =ϕ1 (z), y =ϕ2 (z), z = Z ) уравнение (8.43)
принимает вид
X 2 +Y 2 =ϕ2 (Z) +ϕ
2 (Z).
(8.44)
1
2
Уравнение
(8.44)
является уравнением
поверхности, полученной
вращением линии (8.42) вокруг оси Oz.
Если обозначить текущие координаты точки поверхности буквами х, у, z уравнение (8.44) можно переписать так:
х2 + у2 =ϕ12 (z) +ϕ22 (z).
(8.45)
212
Обратно, если задано уравнение
x2 + y 2 = f (z),
(8.46)
где f (z) ≥ 0 , то оно определяет поверхность вращения, так как в сечении ее плоскостью z = h будет окружность
x2 + y2 = f (z), z = h .
(8.47)
8.10 Поверхности второго порядка
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Геометрическое исследование поверхностей второго порядка проведем по заданным уравнениям с помощью метода параллельных сечений.
1
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой прямоугольной
системе, координат определяется уравнением
x2
+
y2
+
z2
=1.
(8.48)
a2
b2
c2
Уравнение (8.49) называется каноническим уравнением эллипсоида.
Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Оху. Каждая из таких плоскостей определяется уравнением вида z = h , где h — любое число, а линия, которая получается в сечении, определяется двумя уравнениями
x2
y 2
h2
+
=1 −
,
(8.49)
b2
c2
a 2
z
= h.
Исследуем систему уравнений (8.45) при различных значениях h .
1) Если
h
> c (c > 0) , то
x2
+
y 2
< 0 и уравнения (8.49) определяют
a 2
b2
мнимый эллипс, т.е. точек пересечения плоскости z = h с данным эллипсоидом не существует.
2) Если h = ±c , то
x 2
+
y 2
= 0
линия (8.49) вырождается в точки
(0;
a 2
b2
0; +с) и (0; 0; — с) (плоскости z = ±c касаются эллипсоида).
3)Если h < c , то уравнения (8.49) можно представить в виде
x 2
+
y 2
=1,
*2
*2
a
b
z = h.
Откуда следует, что плоскость z = h пересекает эллипсоид по эллипсу с полуосями a* = a 1 − h2 / c 2 , b* = b 1 − h2 / c 2 .
213
При уменьшении h значения а* и b* увеличиваются и достигают своих
наибольших значений при h = 0 , т.е. в сечении эллипсоида координатной плоскостью Оху получается самый большой эллипс с полуосями а*=а и b*=b.
Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz.
Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рисунок 97). Величины а, b, с называются полуосями эллипсоида. В случае а=b=с эллипсоид является сферой.
Рисунок 97
2 Однополостный гиперболоид
Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
x2
+
y2
−
z2
=1.
(8.50)
a2
b2
c2
Уравнение (8.50) называется каноническим уравнением однополостного гиперболоида.
Установим вид поверхности (8.50). Для этого рассмотрим сечения ее координатными плоскостями Oxz (у =0) и Oyz (х=0). Получаем соответственно уравнения
x2
z2
y2
z 2
−
=1,
−
=1,
c2
c2
a2
и b2
y = 0.
x = 0.
из которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z = h , параллельными координатной плоскости Оху. Линия, получающаяся в сечении, определяется уравнениями
2
2
2
2
y
2
x
+
y
=1 +
h
,
x
+
=1,
(8.51)
2
2
2
b
c
или
*2
b
*2
a
a
z
= h.
z = h.
из которых следует, что плоскость
z = h
пересекает гиперболоид по эллипсу с
полуосями a* = a 1 + h2 / c2 , b* = b 1 + h2 / c2 , достигающими своих наименьших
значений при h = 0 , т. е. в сечении данного гиперболоида координатной плоскостью Оху получается самый маленький эллипс с полуосями а*=а и b*=b. При бесконечном возрастании h величины a* и b* возрастают бесконечно.
214
Taким образом, рассмотренные сечения позволяют изобразить однополостный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Оху (рисунок
98).
Рисунок 98
Величины a, b, c называются полуосями однополостного гиперболоида, первые две из них изображены на рисунке 98, а чтобы изобразить на чертеже полуось с, следует построить основной прямоугольник какой-нибудь из гипербол.
3 Двуполостный гиперболоид
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
x2
+
y2
−
z2
= −1.
(8.52)
a2
b2
c2
Уравнение (8.52) называется каноническим уравнением двуполостного гиперболоида.
Установим геометрический вид поверхности (8.52). Для этого рассмотрим ее сечения координатными плоскостями Оxz и Oyz. Получаем соответственно уравнения
x2
z 2
y2
z 2
−
= −1,
−
= −1,
c2
c2
a2
и b2
y = 0.
x = 0.
из которых следует, что в сечениях получаются гиперболы.
Теперь рассмотрим сечения данного гиперболоида плоскостями z = h , параллельными координатной плоскости Oxу. Линия, получающаяся в сечении, определяется уравнениями
2
2
2
2
y
2
x
+
y
=
h
−1,
x
+
=1,
(8.53)
2
2
2
b
c
или
*2
b
*2
a
a
z
= h.
z = h,
215
из которых следует, что при h > c (c > 0) плоскость z = h пересекает
гиперболоид по эллипсу
с полуосями a* = a h2 / c 2 −1, b* = b h2 / c 2 −1 . При
увеличении
h
величины
а* и b* также увеличиваются.
При h = ±c уравнениям (8.53) удовлетворяют координаты только двух точек: (0; 0; -с)и (0; 0; +с) (плоскости z = ±c касаются данной поверхности).
При h < c | уравнения (8.53) определяют мнимый эллипс, т.е. точек
пересечения плоскости z = h с данным гиперболоидом не существует.
Таким образом, рассмотренные сечения позволяют изобразить двуполостный гиперболоид как поверхность, состоящую из двух отдельных «полостей» (отсюда название двуполостный), каждая из которых имеет вид бесконечной выпуклой чаши (рисунок 99).
Рисунок 99
Величины а, b, с называются полуосями двуполостного гиперболоида. На рисунок 99 изображена величина с. Чтобы изобразить на чертеже а и b, нужно построить основные прямоугольники гипербол в плоскостях Oxz и Оуz.
4 Эллиптический параболоид
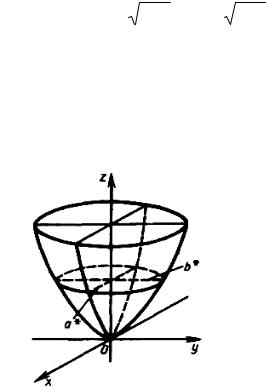
Эллиптический параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
x2
+
y2
= 2z,
(8.54)
p
q
где p > 0, q > 0.
Уравнение (8.54) называется каноническим уравнением эллиптического параболоида.
Исследуем с помощью сечений эту поверхность. Рассмотрим сначала сечения данной поверхности координатными плоскостями Oxz и Oyz. Получаем соответственно уравнения
216
x2 = 2 pz,
y 2 = 2qz,
y = 0.
и
x = 0,
из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат. Теперь рассмотрим сечения данного параболоида плоскостями z = h , параллельными координатной плоскости Оху. Линия, получающаяся в сечении, определяется уравнениями
2
2
2
y
2
x
+
y
=
2h,
x
+
=1,
(8.55)
p
q
или
*2
*2
z = h.
a
b
z = h,
из которых следует,
что при
h
> 0
плоскость z = h
пересекает эллиптический
параболоид по эллипсу с полуосями
a* = 2hp, b* =
2hq . При увеличении h
величины а* и b* также увеличиваются; при h = 0 эллипс вырождается в точку (плоскость z = 0 касается данного параболоида). При h < 0 уравнения (8.55) определяют мнимый эллипс, т. е. точек пересечения плоскости z = h с данным параболоидом не существует.
Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечной выпуклой чаши (рисунок 100).
Рисунок 100
Точка (0, 0, 0) называется вершиной эллиптического параболоида; числа
ри q – его параметрами.
Вслучае p=q уравнения (8.55) определяют окружность с центром на оси Оz, т. е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг ее оси. Такая поверхность называется
параболоидом вращения.
5 Гиперболический параболоид
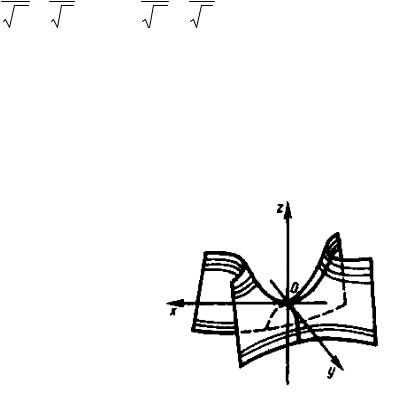
Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
217
x2
−
y2
= 2z,
(8.56)
p
q
где p > 0, q > 0.
Уравнение (8.56) называется каноническим уравнением гиперболического параболоида.
Установим геометрический вид поверхности (8.56). Рассмотрим сечение параболоида координатной плоскостью Oxz ( у = 0) . Получаем уравнения
x2 = 2 pz,
y = 0,
из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси 0z, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Охz ( у = h) , получаются
также направленные вверх параболы
h
2
x2
= 2 p z
+
,
2q
y = h.
сечение данного параболоида плоскостью Oyz (x = 0) .
Рассмотрим
Получаем уравнения
y 2
= −2qz,
x = 0,
из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Оz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x = h) , получим уравнения
h
2
y 2
= −2q z −
,
2 p
x = h,
из которых
следует,
что
при
любом
h в сечении
получается парабола,
направленная вниз.
плоскостями z = h ,
Рассмотрим,
наконец,
сечения
параболоида
параллельными плоскости Оху. Получим уравнения
x 2
y 2
x 2
y 2
или
2 ph
− 2qh =1,
p − q = 2h,
z = h
z = h,
из которых следует, что при h > 0 в сечении получаются гиперболы, пересекающие плоскость Охz; при h < 0 — гиперболы, пересекающие плоскость Оуz; при h = 0 гипербола вырождается в пару пересекающихся прямых
218
x
−
y
= 0,
x
+
y
= 0,
p
q
p
q
и
z = 0
z = 0.
Таким образом, рассмотренные сечения позволяют изобразить гиперболический параболоид в виде седлообразной поверхности (рисунок 101). На рисунке изображено несколько сечений параболоида плоскостями z = h для случаев h > 0 и h < 0 .
Точка (0, 0, 0) называется вершиной гиперболического параболоида; числа
р и q — его параметрами.
Рисунок 101
6 Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением
x2
+
y2
−
z2
= 0 .
(8.57)
a2
b2
c2
Уравнение (8.57) называется каноническим уравнением конуса второго порядка.
Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Оxz ( у = 0) получаем линию
x2
z 2
− c2
= 0,
a 2
y = 0,
распадающуюся на две пересекающиеся прямые
x
z
x
z
−
= 0,
+
= 0,
и
a
c
a
c
y = 0
y = 0.
Аналогично, в сечении конуса плоскостью Оуz (x = 0) также получаются две пересекающиеся прямые
219
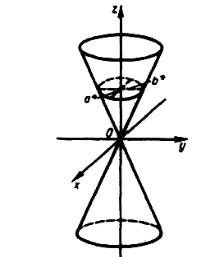
y
z
y
z
− c = 0, и
+ c = 0,
b
b
x = 0
x = 0.
z = h ,
Рассмотрим
теперь сечения
данной
поверхности
плоскостями
параллельными плоскости Оху. Получим уравнения
2
y
2
2
x
2
y
2
x
+
=
h
,
+
=1,
2
2
2
b
c
или
*2
b
*2
a
a
z = h.
z = h,
из которых следует, что при h > 0
и h < 0
в сечениях получаются эллипсы с
полуосями a* =
a
h
,
b* =
b
h
. При увеличении абсолютной величины h полуоси
c
c
а* и b* также увеличиваются.
При
h = 0
линия
пересечения поверхности с
плоскостью
z = h
вырождается в точку (0, 0, 0).
Таким образом, рассмотренные сечения позволяют представить конус в виде поверхности, изображенной на рисунке 102
Рисунок 102
8.11 Вопросы для самоконтроля
1
Сформулируйте определение аффинной системы координат в
пространстве.
2
Сформулируйте определение координат точки
относительно
аффинного репера.
3
Как найти координаты вектора по координатам точек его начала и
конца?
4Запишите формулы для нахождения координат точки, делящей отрезок в отношении λ.
5Сформулируйте определение прямоугольной декартовой системы координат в пространстве.
6Запишите формулу для нахождения расстояния между точками.
220
7Запишите уравнение поверхности в прямоугольной декартовой системе координат.
8Запишите уравнение сферы.
9Как определяется уравнение линии в пространстве?
10Запишите уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
11Запишите общее уравнение плоскости в пространстве.
12Как расположены плоскости Ax + D = 0, By + Cz = 0 в пространстве?
13Запишите уравнение плоскости , проходящей через три точки
14Запишите уравнение плоскости «в отрезках».
15По какой формуле определяется угол между плоскостями?
16Запишите условия параллельности и перпендикулярности двух плоскостей.
17По какой формуле можно найти расстояние от точки дот плоскости?
18Запишите параметрические уравнения прямой в пространстве.
19Запишите общее уравнение прямой в пространстве.
20Запишите формулу для нахождения угла между прямыми в пространстве.
21Запишите условия параллельности и перпендикулярности двух прямых в пространстве.
22По какой формуле можно найти угол между плоскостью и прямой?
23Сформулируйте определение цилиндрической поверхности.
24Сформулируйте определение эллипсоида и запишите его каноническое уравнение.
25 Изобразите следующие поверхности
x2
+
y 2
−
z 2
= 0,
x2
+
y2
= 2z .
a 2
b2
c2
p
q
26Какая кривая будет в сечении у двуполостного гиперболоида, если рассечь его плоскостью z = h ?
27Какие поверхности относятся к цилиндрам второго порядка?
28Сформулируйте определение гиперболического параболоида и запишите его каноническое уравнение.
29Какая кривая будет в сечении у конуса второго порядка, если рассечь его плоскостью у = 0 ?
30Какая кривая будет в сечении у эллипсоида, если рассечь его плоскостью z = h ?
1 
1 
