Глава IX. Неопределенный интеграл

§ 1. Непосредственное интегрирование. Замена переменной и интегрирование по частям

1. Непосредственное интегрирование. Функция F (х) называется первообразной для функции f (x), если F'(x) = f(x) или dF (x) = f (x) dx.

Если функция f(х) имеет первообразную F(х), то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении F(x) + С, где С — постоянная.

Неопределенным интегралом от функции f (х) (или от выражения f(х)dx) называется совокупность всех ее первообразных. Обозначение:

Здесь — знак интеграла, f(х) — подынтегральная функция, f (x) dx — подынтег­ральное выражение, х — переменная интегрирования.

Отыскание неопределенного интеграла называется интегрированием функции.

Свойства неопределенного интеграла

(правила интегрирования)

1^o. 4^o. , где а — постоянная.

2^o. 5 ^o.

3^o. 6 ^o. Если и u=φ(x), то

Таблица основных интегралов

I. . VIII.

II. при m≠-1. IX.

Ш. . X.

IV. . XI.

V. XII.

VI. . XIII.

VII. XIV.

XV.

1328. Найти интеграл .

Решение. Используя свойства 4° и 5°, получаем

.

К первым трем интегралам правой части применим формулу II, а к четвер­тому интегралу—формулу I:

▲

1329. Найти интеграл

Решение.

▲

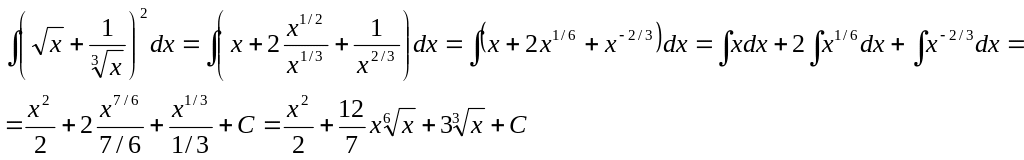
1330. Найти интеграл .

Решение.

Имеем

Свойство 6° позволяет значительно расширить таблицу основных интегралов с помощью приема подведения функции под знак дифференциала. ▲

1331. Найти интеграл .

Решение.

Этот интеграл можно привести к формуле II, преобразовав его так:

Теперь в качестве переменной интегрирования мы имеем выражение 1-f-x² и относительно этой переменной получается интеграл от степенной функции, Сле­довательно,

▲

1332. Найти интеграл

Решение.

Здесь, поступая так же, как и в предыдущем примере, имеем

▲

1333. Найти интеграл .

Решение.

Выражение можно записать как d (ln t), поэтому

▲

1334. Найти интеграл .

Решение.

Заданный интеграл можно представить так:

,

но , а потому

,

т. е. переменной интегрирования является Зсоsх. Следовательно, интеграл берется по формуле VI:

. ▲

1335. Найти интеграл

Решение.

Находим

(см. формулы VIII и IX).

▲

1336. Найти интеграл .

Решение.

Имеем

(см. формулы X и XI). ▲

Найти интегралы:

1337. 1338. 1339.

1340. 1341. 1342.

1343. 1344.

1345. 1346.

1347. 1348.

1349. 1350.

1351.

2. Замена переменной в неопределенном интеграле. Замена переменной в неоп­ределенном интеграле производится с помощью подстановок двух видов:

1) x = φ(t) где φ(t) - монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид

2) u = ψ(x), где u — новая переменная. Формула замены переменной при такой подстановке: