1422. Найти интеграл .

Решение.

Так как х² + 1 есть двукратный множитель, то

Освобождаясь от знаменателей, получим

Приравняем коэффициенты при одинаковых степенях х:

x^3	1=C
х^2	0=D
x	-2=A+C; A=-3
x^0	0=B+D; B=0

Следовательно,

Заметим, что данный интеграл можно было найти проще с помощью подста­новки х² +1= t. ▲

1423. Найти интеграл

Решение.

Выделим целую часть данной неправильной рациональной дроби:

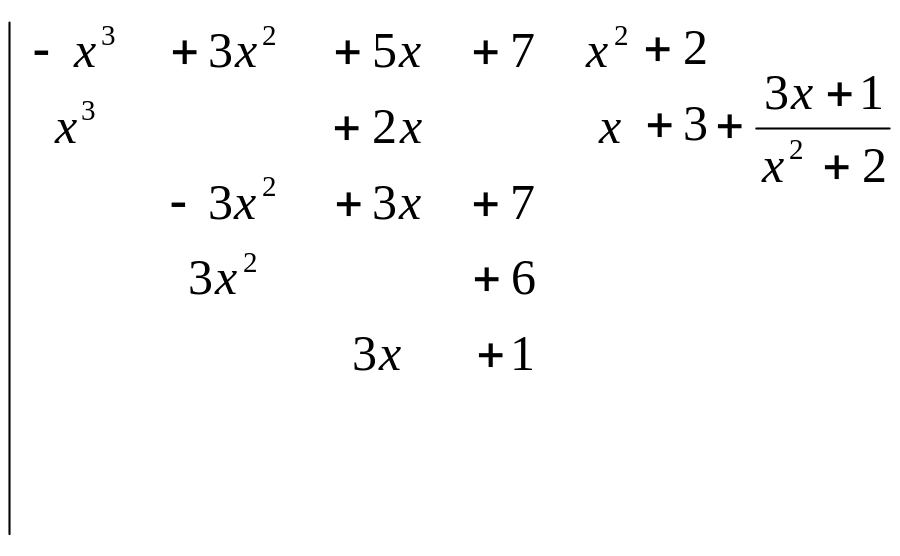
Итак,

Отсюда находим

▲

1424. Найти интеграл

Решение.

Т ак как подынтегральная функция является правильной дробью, то ее следует сразу представить в виде суммы простейших дробей. Легко видеть, что многочлен х³ + 6х²+11х+6 обращается в нуль при х = —1, поэтому он де­лится без остатка на х+1. Выполним деление:

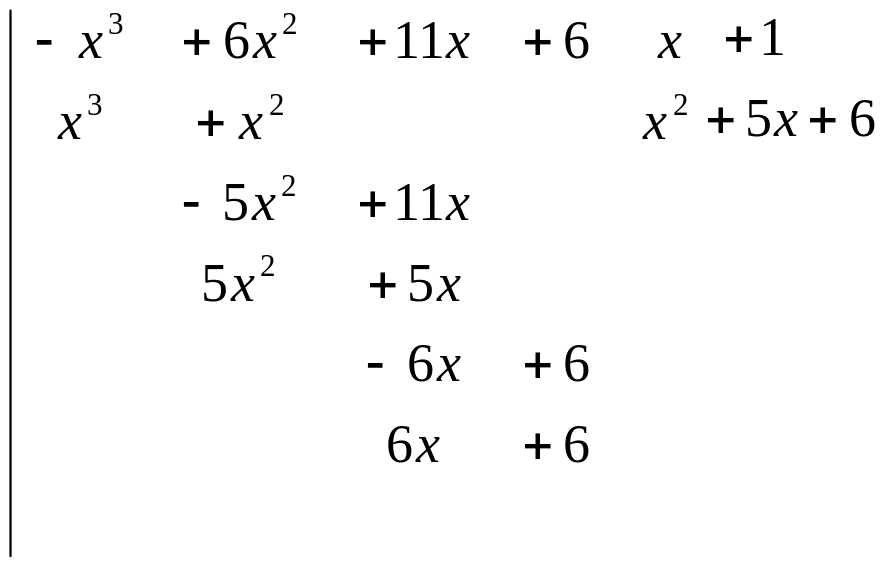
Следовательно,

Освобождаясь от знаменателей, получим

Полагая х=-1, найдем 3=2А, т. е. А = 3/2. Если х= — 2, то получим 2=-В, т. е. В=-2. При х =-3 получим 1=2С, т. е. С=1/2. Итак,

▲

1425. Найти интеграл

Решение.

Прежде всего нужно выделить целую часть:

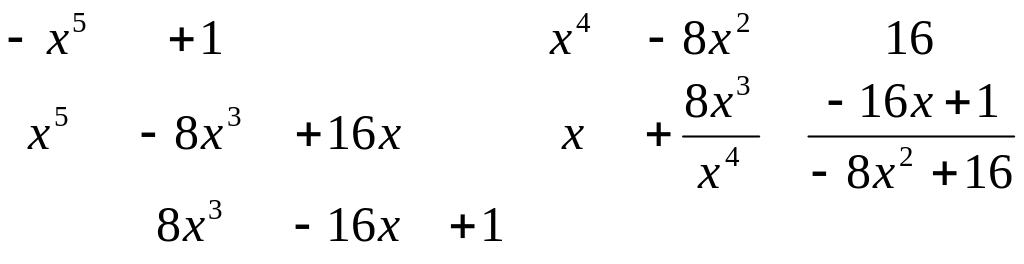
Следовательно,

Разложим теперь правильную дробь на простейшие:

Освободимся от знаменателей:

Полагая х=2, найдем 33=16А, т. е. А = 33/16. При х = — 2 получим — 31 = 16С, т.е. С=— 31/16. Если х = 0, то 1==4А — 8B + 4C + 8D. Заменив А и С их значениями, получаем

или

Для того чтобы найти В и D, составим еще одно уравнение. Сравнив коэф­фициенты при х³, получим 8 = B + D. Решив систему уравнений

находим D= 129/32, B= 127/32.

Итак,

▲

1426. Найти интеграл .

Решение.

Подынтегральная функция является правильной рациональной дробью и можно было бы найти интеграл, представив эту дробь в виде суммы простейших дробей. Однако нахождение интеграла можно значительно упростить, если произвести замену переменной х— 1=t; тогда x = t+1 и dx = dt. В резуль­тате получаем

▲

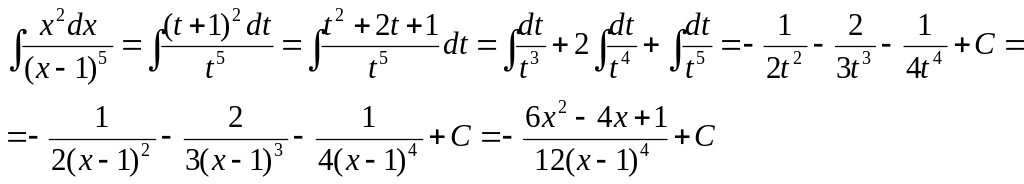
1427. Найти интеграл

Решение. Преобразуем знаменатель: = Теперь имеем

Произведем замену x² + 3 = t тогда 2х dx = dt и

Из последних двух примеров видим, что иногда перед интегрированием ра­циональной дроби следует произвести замену переменной. ▲

Найти интегралы:

1428. 1429.

1430. 1431.

1432. 1433.

1434. 1435.

1436. 1437.

Указание: представить знаменатель в виде

1438. 1439.

1440.

3. Интегралы вида , где R – рациональная функция. С помощью подстановки =t, откуда dx=dt, dx=dt/ =dt/t, интеграл указанного вида преобразуется в интеграл от рациональной функции