1441. Найти интеграл

Решение: положим =t; тогда dx=dt, dx=dt/t, откуда

так как , то разложение простейшей дроби имеет вид

освобождаясь от знаменателей получим

если t=0, то 1=-3А, т.е. А=-1/3, если же t=-t, то 2=4В, т.е. В=1/2, наконец, если t=3, то 31=12С, т.е. С=31/12

Итак,

и значит

▲

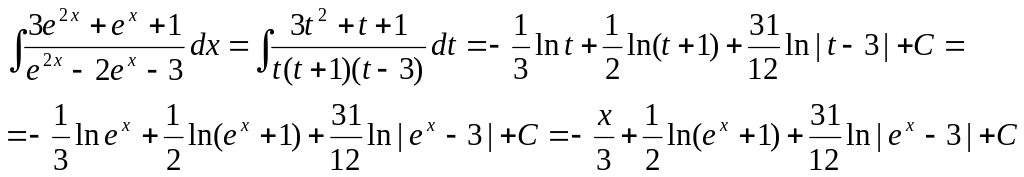
Найти интегралы:

1442.

1443.

§ 3. Интегрирование простейших иррациональных функций

1. Интегралы вида где R — ра­циональная функция; m₁, n₁, m₂, n₂, ...—целые числа. С помощью подста­новки ax+b = t^s, где s — наименьшее общее кратное чисел n₁, n_2..., указанный интеграл преобразуется в интеграл от рациональной функции.

1444. Найти интеграл

Решение. Здесь n₁ = 3, n₂= 2; поэтому s = 6. Применим подстановку 2x+1=t⁶, тогда x = (t⁶—l)/2, dx — Sfldt и, следовательно,

Возвращаемся к старой переменной. Так как t = (2x+1)^1/6, то

▲

2. Интегралы вида Такие интегралы путем выделения полного квадрата из квадратного трехчлена приводятся к табличным интегралам XX или XXI.

1445. Найти интеграл

Решение.

Преобразуем квадратный трехчлен к виду . Тогда

▲

1446. Найти интеграл

Решение.

Имеем

▲

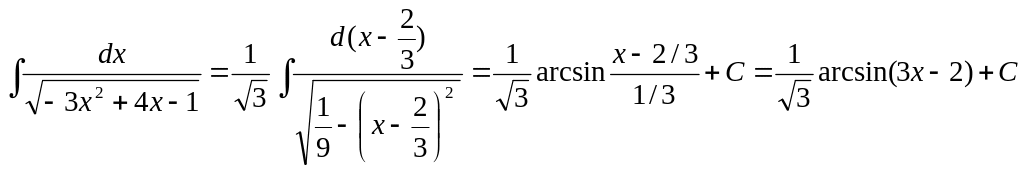3. Интегралы вида Для нахождения этого интеграла выделим в числителе производную квадратного трехчлена стоящего под знаком корня, и разложим интеграл на сумму двух интегралов:

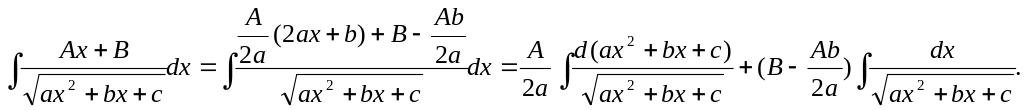
Первый из полученных интегралов есть табличный интеграл XVII, а второй рассмотрен в п. 2. § 3.

1447. Найти интеграл

Решение.

Выделим в числителе производную подкоренного выражения:

▲

1448. Найти интеграл .

Решение.

Имеем

▲

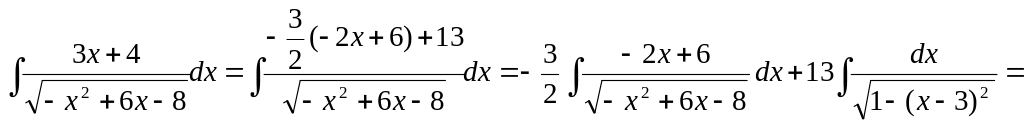
4. Интегралы вида С помощью подстановки x-α=1/t этот интеграл приводится к рассмотренному в п. 2.

1449. Найти интеграл

Решение.

Положим x=1/t, тогда dx = — (1/t²) dt и

▲

1450. Найти интеграл

Решение.

Полагаем x-1 =1/t, тогда x= 1/t+1 и dx = —(1/t²) dt. Следо­вательно,

▲

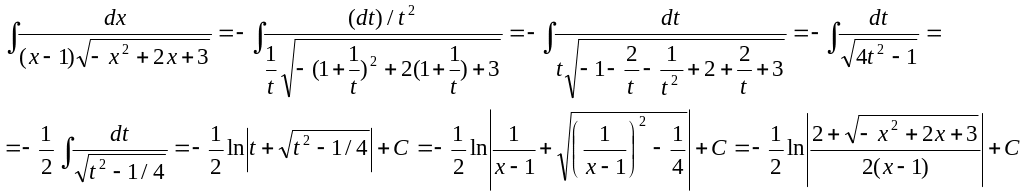1451. Найти интеграл

Решение.

Записав числитель подынтегральной функции в виде 3x+2 = 3(x+1) —1, получим

Представим данный интеграл как разность двух интегралов:

К первому интегралу применим формулу XXI, а ко второму —подстановку x+1=1/t:

▲

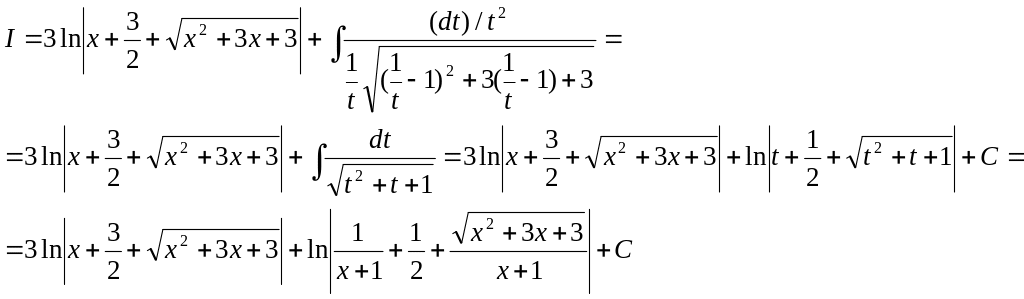
5. Интегралы вида

где Р_n (х) — многочлен n-й степени. Интеграл такого вида находится с помощью тождества:

где Q_n-1 (x) —многочлен (n —1)-й степени с неопределенными коэффициентами, λ — число.

Дифференцируя указанное тождество и приводя результат к общему знаменателю, получим равенство двух многочленов, из которого можно определить коэффициенты многочлена Q_n-1 (x) и число λ..

1452. Найти интеграл

Решение.

Здесь n = 3, поэтому соответствующее тождество имеет вид

Дифференцируя обе его части, получаем

Освобождаемся от знаменателя:

или

Сравнивая коэффициенты при одинаковых степенях x, получим

.

Решая систему, найдем b₀=1/3, b₁=l/6, b₂ = 7/6, λ = 5/2. Следовательно,

▲

Найти интегралы:

1453. 1454.

1455. 1456.

1457. 1458.

1459. 1460.

1461. 1462. .

6. Интегралы от дифференциальных биномов , где m, n, p — рациональные числа. Как доказал П. Л. Чебышев, интегралы от дифферен­циальных биномов выражаются через элементарные функции только в трех случаях:

1) р —целое число, тогда данный интеграл сводится к интегралу от рациональной функции с помощью подстановки x = t^s, где s — наименьшее общее кратное знаменателей дробей т и п,

2) (т +1)/п — целое число; в этом случае данный интеграл рационализируется с помощью подстановки a + bxⁿ = t^s;

3) (m+l)/n+p —целое число; в этом случае к той же цели ведет подстановка ах^-n+b= t^s, где s — знаменатель дроби р.