
- •1. Учет погрешности вычислений.
- •3. Приближенные вычисления без учета погрешности.
- •7. Метод границ
- •8.Математические модели и численные методы.Вспомогательные сведения из математического анализа. Метод оптимального исключения решения слау.
- •9. Решение ур-ний с одним неизвестным. Дихотомия. Принцип Банаха.
- •13. Метод Гаусса.
- •14. Обращение матриц и уточнение приближенной обратной матрицы.
- •15. Метод квадратного корня решения слау.
- •19. Интерполирование функций. Интерполяционный многочлен Лагранжа.
- •20. Интерполирование функций. Конечные разности. Разделённые разности.
- •21. Интерполяционные многочлены Ньютона.
- •22. Численное дифференцирование. Некоторые частные формулы вычисления производных.
- •23. Обработка результатов эксперимента. Метод наименьших квадратов.
- •24. Численное интегрирование. Квадратурные формулы Ньютона-Котеса.
- •26. Численное интегрирование. Квадратурная формула Симпсона.
- •27. Численное интегрирование. Квадратурные формулы прямоугольников. Правило Рунге выбора шага интегрирования.
24. Численное интегрирование. Квадратурные формулы Ньютона-Котеса.
Точное вычисление определенных интегралов по формуле Ньютона-Лейбница выглядит так:
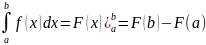 ,
где F(x)
– первообразная для f(x),
т.е.
,
где F(x)
– первообразная для f(x),
т.е.
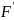 (x)=f(x).
(x)=f(x).
Использование этой формулы не всегда предоставляется возможным, т.к. первообразная подынтегральной ф-ции не всегда выражается в интегральных ф-ях – не берущийся интеграл, или не целесообразно,т.к. нахождение первообразной часто связано с очень громоздкими преобразованиями. В этих случаях, а так же, когда подынтегральная ф-ция задана таблично целесообразно вычислять определенные интегралы приближенно. Существуют различные методы численного интегрирования.
Формулы Ньютона-Котеса.
Пусть
требуется вычислить определенный
интеграл
 Заменим подынтегральную ф-цию ее
интерполяционным многочленом
(x),
т.е. f(x)=
(x)+
Заменим подынтегральную ф-цию ее
интерполяционным многочленом
(x),
т.е. f(x)=
(x)+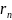 (x),
тогда
(x),
тогда
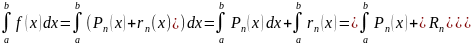 (x)=
(x)=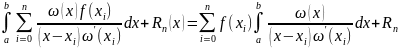 (x)=
(x)=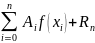 (x),
где
(x),
где
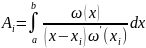 ,
,
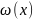 =
=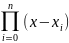
Очевидно,
что коэффициенты
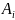 зависят от узлов интерполяции
.
Таким образом, мы можем записать, что
зависят от узлов интерполяции
.
Таким образом, мы можем записать, что
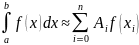 В
этой формуле правая часть называется
квадратурной суммой,
- квадратурные коэффициенты,
– квадратурные узлы.
В
этой формуле правая часть называется
квадратурной суммой,
- квадратурные коэффициенты,
– квадратурные узлы.
В
то же время
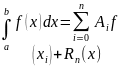 - формула механических квадратур.
- формула механических квадратур.
Введем
новую переменную t=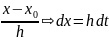
x-
=x-(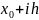 )=(x-
)-ih=th-ih=(t-i)h
)=(x-
)-ih=th-ih=(t-i)h
(x)=(x-
)(x-
)…(x-
)=th(t-1)h*…*(t-n)h=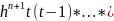 (t-n)=
(t-n)=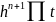 ,
где
,
где
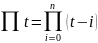
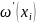 =(
=(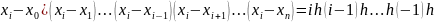 …(i-n)h=(
…(i-n)h=(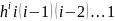 )(
)(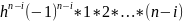 )=
)=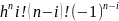
Отсюда получим:
=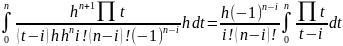 – формула показывает, что квадратурные
коэффициенты
зависят от отрезка интегрирования,
т.к. в формуле присутствует h
(шаг). Введем коэффициенты
– формула показывает, что квадратурные
коэффициенты
зависят от отрезка интегрирования,
т.к. в формуле присутствует h
(шаг). Введем коэффициенты
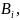 которые будут получаться:
которые будут получаться:
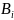 =
=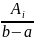 ,
h=
,
h=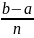 ,
тогда
,
тогда
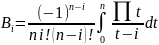
Коэффициенты уже не зависят от h, а только лишь от числа точек разбиения.
Таким образом, окончательно мы можем записать:
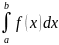 =(b-a)
=(b-a)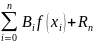 - квадратурная формула Ньютона-Котеса.
- квадратурная формула Ньютона-Котеса.
Коэффициенты носят название коэффициентов Ньютона-Котеса.
25.
Численное интегрирование. Квадратурная
формула трапеций.
Квадратурная формула Ньютона-Котеса
имеет вид:
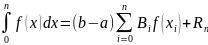 ,
где
,
где
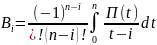 и
и
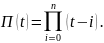 Найдем явный вид коэффициентов
(при
n=1
имеет 2 узла:
Найдем явный вид коэффициентов
(при
n=1
имеет 2 узла:
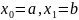 ):
):
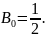 Таким образом, формула трапеции имеет
вид:
Таким образом, формула трапеции имеет
вид:
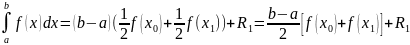 .
.
Выделим
остаточный член для трапеции (
),
если в общем случае
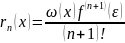 .
В нашем случае
.
В нашем случае
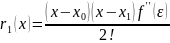 .
Тогда
.
Тогда
 =
=
Если
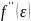 - непрерывна на отрезке [a,b],
то так как множитель
- непрерывна на отрезке [a,b],
то так как множитель
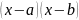 сохраняет знак на этом отрезке, то на
нем существует такая точка η, что
сохраняет знак на этом отрезке, то на
нем существует такая точка η, что
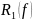 =
=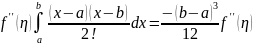 ,
где
,
где
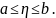 Следовательно,
Следовательно,
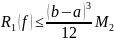 ,
где
,
где
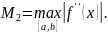
Для
увеличения точности формулы трапеции
разделим отрезок [a,b]
на n
частей длины
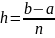 и рассмотрим
и рассмотрим
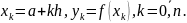 Тогда
общая квадратурная формула трапеции
имеет вид:
Тогда
общая квадратурная формула трапеции
имеет вид:
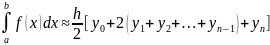 .
.
Остаточный
член формулы имеет вид:
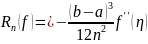
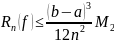 ,
где
,
где
26. Численное интегрирование. Квадратурная формула Симпсона.
Пусть
n=2,
тогда коэффициенты в формуле Ньютона-Котеса
равны
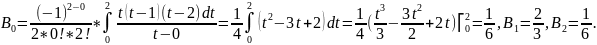 Из формулы Ньютона-Котеса следует
формула Симпсона:
Из формулы Ньютона-Котеса следует
формула Симпсона:
 ,
где
,
где
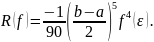
Если
отрезок [a,b]
разбить на четное число n=2m,
тогда
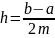 и
и
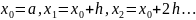
Общая
квадратурная формула Симпсона:
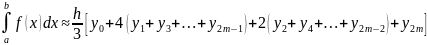 Остаточный
член:
Остаточный
член:
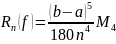 ,
где
,
где
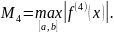
Остаточный
член в формуле трапеции уменьшается
пропорционально величине
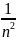 ,
а в формуле параболы -
,
а в формуле параболы -
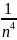 .
Формула Симпсона сущ-но точнее, чем
формулы прямоугольников и трапеций.
.
Формула Симпсона сущ-но точнее, чем
формулы прямоугольников и трапеций.
