21. Интерполяционные многочлены Ньютона.

Интерполяц-ый многочлен Лагранжа, кот. м. построить при любом расположении узлов интерполяции облад. Одним существенным недостатком. Если понадобится увелич ч-ло узлов (след и степень многочлена), то в эт случае мн-н Лагр придётся выч занов, т к кажд его член зависит от узлов интерполирования. Указанным недостатком не обладает интерполяц мн-н Ньютона. 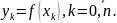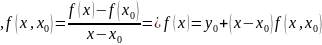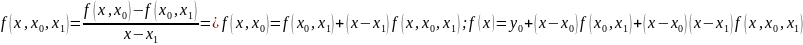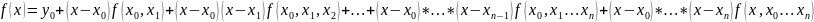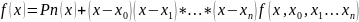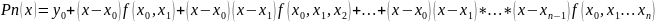Пусть дана ф-ция: y=f(x), причём Из 1-ой разд-ой разности получим Поскольку разделённая разность Т о на n-ом шаге мы получим след: (1) или где (2)

Полагая в (1) получим: След мн-н 2 – интерполяц мн-н д/ ф-ции y=f(x), построенной по n+1 узлам: 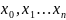мн-н 2 называют интерпол-ым мн-ом Ньютона, подставляя его в общую интерполяц-ую ф-лу, получим: 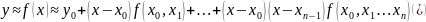В случае равноотстоящих узлов интерполяции: , h-шаг. Из интерпол-ой ф-лы Ньютона с учётом равенств: 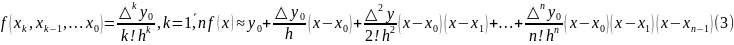Ф-ла (3) получила назв-ие интерполяционная ф-ла Ньютона «интерполирование вперёд». «инт-ие вперёд» объясн-ся тем, что ф-ла сод-ит заданное знач. Ф-ции, соотв-ее узлам интерполяции, находящимся только вправо от узла X0. Ф-ла (3) удобна при интерполир-ии ф-ций д/ знач x, близких к наименьшему узлу x0. Пусть x=x0+ht,тогда 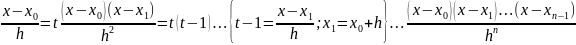. Тогда ф-ла (2) имеет вид: 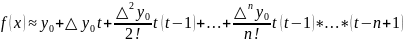(4)

Остаточный член д/ полинома (4) имеет вид: 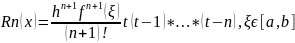Абсолютная погрешность мет по ф-ле Ньютона «интерпол-ие вперёд» определ нерав-ом: 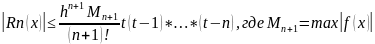[a,b] Интерполяц-ую ф-лу Ньютона (*) т/же м записать: 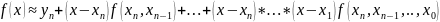В случае равноотстоящих узлов из посл ф-лы аналогично ф-ле Ньютона «и в» м получить ф-лу Н. «инт-ие назад». 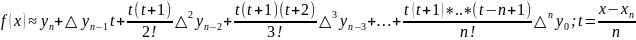ф-лу Н. «инт-ие назад» используют при интерпол-ии ф-ции в т-ах x, близких к наиб узлу xn-ое. Абс погрешность метода «интерп. назад» определ-ся ф-ой:

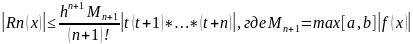
22. Численное дифференцирование. Некоторые частные формулы вычисления производных.

Численное дифференцирование применяется если:

1 функция задана таблично

2 функция задана неудобным для дифференцирования аналитическим выражением

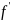Задача численного дифференцирования некорректна – нарушается условие 3 корректности, т.е. нарушается условие непрерывной зависимости решения от входных данных. При численном дифференцировании функцию f(x) заменяют интерполяционным многочленом (x) и считают, что (x) = (x).

близость значений ф-ции f(x) и многочлена (x) не гарантируют близости их угловых коэффициентов и , т.е. близости производных:

f(x)≈ (x)

( )=tg

( )=tg

Пусть на [a,b] рассматривается ф-ция f(x), которая имеет непрерывную производную до (n+1) порядка. Возьмем на [a,b] (n+1) различных узлов , , …, и будем считать, что они расположены в порядке возрастания < <…< .

Пусть f( ) – значение ф-ции y=f(x) в этих узлах , i= . По этим значениям построим интерполяционный многочлен (x), который будет совпадать с ф-ей f(x) в узлах интерполирования, т.е. ( )=f( ), i= . Отсюда f(x)= (x)+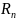 (x), где (x) – погрешность интерполяции. Вычислим производную от ф-ции f(x) порядка m. Получим 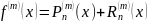и в качестве 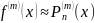. 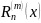будет являться погрешностью численного дифференцирования.

Пользоваться формулой целесообразно тогда, когда m≤n, т.к. при n>m 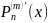=0. Для погрешности справедлива формула: 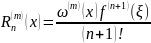. =(x- )(x- )…(x- ). [ ], где [ ] – наименьший отрезок содержащий точки , , x.

Некоторые частные формулы вычисления производных.

Каждая из формул для интерполяции многочлена (Лагранжа, Ньютона) может служить источником для получения различных формул вычисления производных, т.е. формул численного дифференцирования. Таких формул можно получить большое число, но для выяснения идеи их построения ограничимся несколькими примерами.

Например, возьмем в качестве многочлена (x) интерполяционную формулу Ньютона:

(x)=f(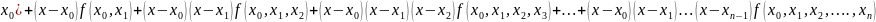

Обозначим через 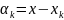. Получим f(x)≈ (x)=f( )+

=

=

=

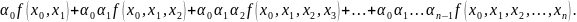
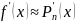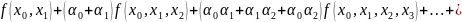
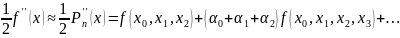
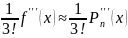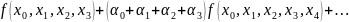
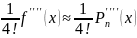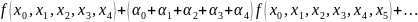
Аналогично можно получить формулы для вычисления производных в случае равноотстоящих узлов, т.е. x= +th, где t=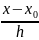 , и возьмем формулу Ньютона интерполирования в нач. табл. или «интерполирования вперед».

f(x)≈ (x)=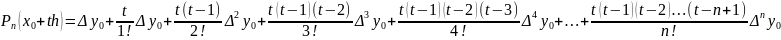

=

=
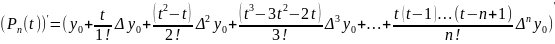
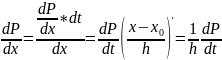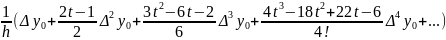
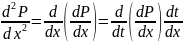