8.2. Построение обобщенного дифференциального уравнения неустановившейся фильтрации однородной жидкости и газа в пористой среде при изотермическом процессе

Дифференциальные уравнения движения сжимаемой однородной жидкости и газа при установившемся неустановившемся изотермическом процессах хорошо известны. Ниже дается упрощенный вывод обобщенного дифференциального уравнения движения, из которого получается ряд уравнений для частных случаев. Кроме того, указаны методы решения и пути использования их в нефтегазопромысловой практике.

8.2.1. Неустановившееся изотермическое движение сжимаемой жидкости в деформируемой пористой среде. Неизвестными функциями являются: давление ; вектор скорости фильтрации ; плотность или удельный объемный вес ; пористость пласта .

Уравнение неразрывности записывается в виде

(8.2.1)

Уравнение состояния для упругой жидкости и пористости суть:

(8.2.2)

Здесь

₀ и т₀ – плотность и коэффициент пористости при начальном давлении Р₀;

β_ж и _с – коэффициенты сжимаемости жидкости и скелета пористой среды.

Введем обобщенную функцию и продифференцируем ее:

(8.2.3)

С учетом (8.2.2) и (8.2.3) уравнение (8.2.1) принимает вид

(8.2.4)

Здесь

^* – коэффициент упругоемкости пласта.

Рассмотрим некоторые частные случаи.

1. Движение плоскорадиальное неустановившееся, жидкость вязкая упруго-капельная, пласт однородный: (Р)=₀=const; (Р)==const; K_i(P)=K=const. Из уравнения (8.2.4) следует известное уравнение пьезопроводности

(8.2.5)

Здесь

æ – коэффициент пьезопроводности пласта.

2. Движение неустановившееся, плоскорадиальное, пласт однородно-анизотропный (К_r/К_z). Уравнение (8.2.4) принимает вид

(8.2.6)

æ^* – коэффициент анизотропии пласта.

3. Движение установившееся, жидкость несжимаемая: (Р)=₀=const; дР/dt=0. Из уравнения (8.2.4) следует известное уравнение Лапласа .

4. Движение неустановившееся, жидкость упруго-капельная, вязкопластичная, (Р)=₀=const. Коэффициент подвижности K/ есть [23]

(8.2.7)

где

К₀ и ₀ – параметры для вязкопластичной жидкости с ослабленными структурно-механическими свойствами, т. е. когда создаваемый градиент сдвига достиг второго начального предельного градиента (grad P₊₊) [23].

С учетом выражений (8.2.3) и (8.2.7) уравнение (8.2.4) запишется в виде

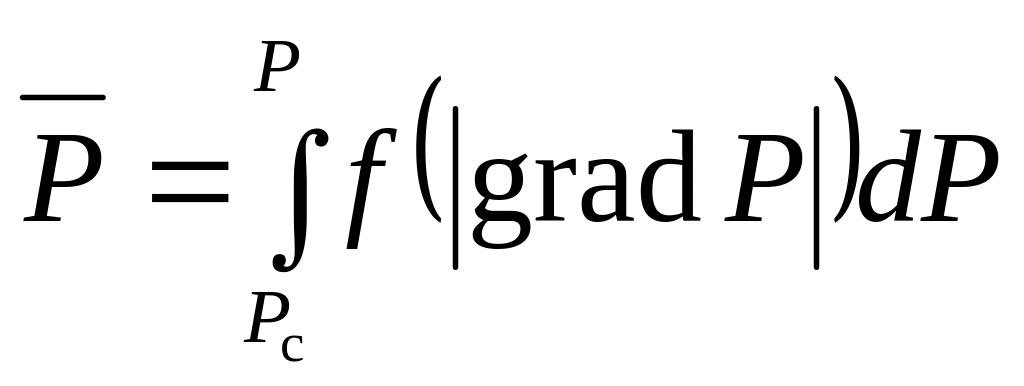; ; . (8.2.8)

Для функции (10.2.7) предложены различного вида аппроксимации. Б.И. Султанов для вязкопластичной жидкости предложил соотношение

(10.2.9)

где

– предельный перепад давления сдвига, определяемый по экспериментальным данным;

Р₀ – предельное давление сдвига;

Р и Р_с – пластовое и забойное давление.

Взяв производную функцию (8.2.8) с учетом выражения (8.2.9), из уравнения (8.2.8) получаем

(8.2.10)

Как видим, уравнение (8.2.10) нелинейное и требует численного интегрирования. Линеаризация этого уравнения, очевидно, возможна при режиме пласта Тогда уравнение (8.2.10) представляет собой уравнение пьезопроводности, решение которого хорошо известно. Переход к давлению после нахождения функции можно осуществить по формуле, получаемой интегрирование функции (8.2.8) с учетом выражения (8.2.9) в пределах от Р₀ до Р:

. (8.2.11)

Нетрудно видеть, что при из формулы (8.2.11) следует а уравнение (8.2.10) обращается в уравнение пьезопроводности. Предложены также более точные аппроксимации функции (8.2.7), интерпретация которых может быть произведена аналогичным образом [23].

Для установившегося движения из уравнения (8.2.8) следует уравнение Лапласа для функции , т. е. .

8.2.2. Изотермическая фильтрация реального газа. Принимается: температура пласта постоянной, Т=const; коэффициент сверхсжимаемости газа Z=Z(P,T); коэффициент вязкости =(Р,Т); коэффициенты проницаемости K=const и пористости т₀=const. Тогда, учитывая уравнение состояния реального газа и обобщенную функцию (8.2.3), из уравнения неразрывности (8.2.1) получаем

(8.2.12)

Преобразуя уравнение (8.2.12) с учетом дифференциала dР, находим

(8.2.13)

Нелинейное уравнение (8.2.13) является основным дифференциальным уравнением фильтрации газа и носит название обобщенное уравнение Лейбензона. Одним из методов решения подобных уравнений является метод линеаризации, широко освещенный в литературе [6 и др.]. Если усреднить и , то из формулы для Р (8.2.12) следует известная функция Лейбензона, подстановка которой в уравнение (8.2.12) дает

(8.2.14)

Получили нелинейное дифференциальное уравнение Лейбензона для фильтрации идеального газа, аналогичное уравнению Буссинеска.

Разделив левую и правую части уравнения (8.2.14) на удельный объемный вес , получаем:

(8.2.15)

где

Н – напор;

С – коэффициент фильтрации;

У – высота положения.

Уравнение (8.2.15) носит название дифференциального уравнения гидравлической теории нестационарного безнапорного притока Буссинеска. Одним из методов решения подобных уравнений является метод линеаризации Лейбензона [6].

В связи с открытием месторождений природного газа, в смеси которого содержится большое количество кислых компонентов, таких как сероводород, углекислый газ, азот, возникает необходимость учета реальных свойств газа при обработке КВД и определении параметров пласта. С учетом реальных свойств газа для случая K_i=K=const функцию (8.2.12) можно преобразовать к следующему виду:

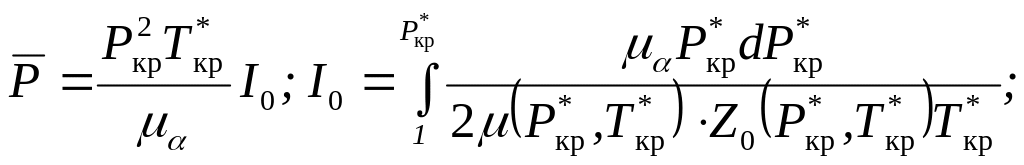(8.2.16)

(8.2.17)

где

– приведенные критические давление и температура;

_см – коэффициент динамической вязкости смеси природного газа в атмосферных условиях;

₀ – поправка на вязкость за счет содержания компонентов;

α – поправка на сжимаемость газа, учитывающая содержание в смеси кислых компонентов.

Имея опытные данные для определения коэффициентов вязкости и сверхсжимаемости, можно рассчитать функцию (8.2.16). Результаты таких расчетов путем численного интегрирования функции J₀ приведены в диапазоне параметров: концентрация компонентов (СО₂+H₂S)=1060% [24, 24а].

8.2.3. Фильтрация газоконденсатной смеси. Для гомогенной жидкости уравнения (8.2.8) записываются в виде:

(8.2.18)

,

где

(8.2.19)

(8.2.20)

Н^* – потенциальная функция Лейбензона-Христиановича;

K_к () и K_г () – фазовые проницаемости для конденсата и газа, как функции конденсатонасыщенности ;

_к; _г – коэффициенты абсолютной вязкости конденсата и газа в пластовых условиях;

_см – плотность газоконденсатной смеси в пластовых условиях;

_г – насыщенность пористой среды газом;

В_к и В_г – объемные коэффициенты фаз;

_гк – коэффициент растворимости газа в конденсате;

– потенциальные функции, соответствующие давлениям начала конденсации Р_нк и на забое скважины Р_с.

Уравнения (8.2.8), (8.2.10), (8.2.13), (8.2.14) и (8.2.15) могут быть записаны в цилиндрических координатах по аналогии с уравнением (8.2.6).

8.2.4. Обобщение уравнений. Неустановившийся приток к несовершенной скважине. Анализируя приведенные уравнения можно заметить, что структура и методы решения их одинаковы. Это позволяет обобщить их в одно уравнение для однородной «фиктивной» жидкости с некоторой «фиктивной» потенциальной функцией Ф. Тогда, согласно В.Н. Щелкачеву [25], обобщенное уравнение фильтрации может быть записано в унифицированной форме

(8.2.21)

Отсюда следует:

а) при =0, =Х и j=0 — уравнение для прямолинейного одномерного потока

(8.2.22)

б) при =1, =r и j=1 — уравнение притока в цилиндрических координатах

(8.2.23)

в) при =2, =r и j=0 — уравнение для сферического потока

(8.2.24)

Как известно [8], в области, содержащей стоки (источники), потенциал  удовлетворяет уравнению Пуассона =(x,y,z,t), где  – оператор Лапласа,  – плотность стока. Тогда для потенциала точечного стока можно использовать уравнение (8.2.21), добавив в левую часть слагаемое:

(8.2.25)

где

q₀ – интенсивность стока;

(r) – функция Дирака [8];

q(t) – некоторая функция времени.

Для притока к точечному стоку с координатами r=0, z=, расположенному в круговом осессиметричном однородно-анизотропном пласте конечного радиуса, уравнение (8.2.23) с учетом (8.2.25) записывается в виде

(8.2.26)

Решения приведенных уравнений широко освещены в задачах подземной гидрогазодинамики и теории разработки нефтяных, газовых и газоконденсатных месторождений для плоского течения. Здесь мы покажем использование полученных уравнений для решения задач неустановившейся пространственной фильтрации жидкости на основе теории потенциала точечного стока-источника.

Для линии стоков, частично вскрывающей (несовершенная скважина по степени вскрытия) бесконечный по протяженности однородный пласт в интервале и конечный по толщине h (Рис.8.1а) получено следующее решение для понижения забойного давления в безразмерных параметрах [28]:

, (8.2.27)

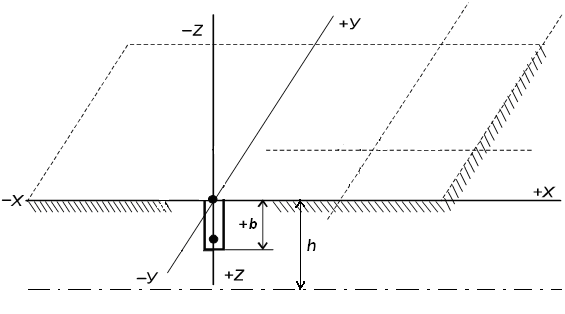
Рис. 8.1а. Схема притока к несовершенной линии стоков