1.2.1. Дискретные случайные величины

СВ называется дискретной, если множество ее возможных значений счетное или конечное, т. е. пространство исходов конечно. Общими формами представления распределения для дискретной СВ являются:

1) ряд распределения;

2) функция распределения.

Рядом распределения P(z) дискретной СВ Zназывают таблицу, в которой перечислены возможные значения СВ и соответствующие им вероятности (табл.1.3).

Таблица 1.3. Ряд распределения СВ

			...
			...

Здесь .

Функцией распределениядискретной СВ называют функциюF(z), равную вероятностиP(Z < z)того, что СВ будет меньше произвольно выбранного значенияz. Функция распределенияF(z)вычисляется по формуле

,

(1.19)

где суммирование ведется по всем значениям i, для которых .Таким образом,F(z) является функцией накопления вероятностей.

Вероятность попадания СВ Zв интервал (a,b) выражается формулой

P(a < Z < b) = F(b) – F(a).

(1.20)

Пример 1.8. При десятикратном подбрасывании игральной кости получены следующие результаты: «1» выпала 2 раза, «2»  1 раз,«3»4 раза, «4»2 раза, «5»0 раз, «6»1 раз. Требуется определить функцию распределения случайной величины – выпадения некоторого количества очков на игральной кости.

Решение. Вероятность выпаденияkочков определим по формуле, гдеkколичество исходов, в которых зафиксировано выпадениеkочков. Значения функции распределения вероятности выпаденияkочков определим как сумму.

Результаты сведем в табл.1.4.

Таблица 1.4. Распределения вероятности

k	1	2	3	4	5	6
	0,2	0,1	0,4	0,2	0	0,1
F(k)	0	0,2	0,3	0,7	0,9	0,9

Полученные значения вариационного ряда и функции распределения представим графически на рис.1.1 и 1.2 соответственно.

F(k)

Рис.1.1. Вариационный ряд Рис.1.2. Функция распределения

Определение распределения вероятностей СВ в виде вариационного ряда или функции распределения дает полное представление о СВ. В то же время для практических расчетов в ряде случаев достаточно знать лишь некоторые параметры этого распределения, называемые моментами.Математическим ожиданием M[Z] СВZназывается ее среднее значение, вычисленное по формуле

.

(1.21)

Начальным моментомk-го порядкаСВZназывают математическое ожиданиеk-й степени этой СВ:

.

(1.22)

Следовательно,

.

(1.23)

ЦентрированнойСВ называется разность между СВZи ее математическим ожиданием:

(1.24)

Центральным моментом k-го порядкаСВZназывают математическое ожидание центрированной СВk-й степени:

.

(1.25)

Математическое ожидание СВ Zесть ее первый начальный момент, а дисперсиявторой центральный момент:

.

Дисперсией D[Z] СВZ называют математическое ожидание от квадрата центрированной СВ:

.

(1.26)

Следовательно,

.

(1.27)

При практических расчетах в некоторых случаях удобнее использовать следующую формулу расчета дисперсии, полученную путем преобразования (1.26):

.

(1.28)

Корень квадратный из дисперсии называют средним квадратичным отклонениеми определяют по формуле

,

(1.29)

где имеет размерность случайной величины.

Для определения вероятности события, заключающегося в принятии дискретной СВ определенного значения , необходимо установитьзакон распределения вероятностей и его параметры (моменты). Закон распределения может быть задан рядом распределения или аналитической зависимостью. Наиболее часто встречающиеся аналитические зависимости носят названия типовых законов распределения. Для дискретных СВ типовыми являются законы Бернулли и Пуассона.

1. Дискретная СВ Z, выражающая число появлений события А в n независимых испытаниях, в каждом из которых вероятность появления события А одинакова и равна р, подчиняется закону распределения Бернулли. Вероятность возможного значения Z = k определяется по формуле

,

(1.30)

где q = 1 – pвероятность непоявления события.

2. Если вероятность события мала, а число испытаний велико, то применение формулы Бернулли затруднительно. В этом случае пользуются ее предельным значением распределением Пуассона. Вероятность появления событияАровноkраз вnнезависимых испытаниях определяется приближенно по формуле

,

(1.31)

где  = np параметр распределения Пуассона.

Пример1.9. Необходимо определить неисправный элемент в электрической цепи из 10 последовательно включенных микросхем. Каждая следующая микросхема проверяется в том случае, если предыдущая оказалась исправной. Построить ряд распределения и найти математическое ожидание числа проверок, если вероятность исправности элемента равнар.

Постановка задачи. Испытания заканчиваются наk-м элементе (k = 1,2,...,9), если первыеk – 1пройдут испытания, аk-й не выдержит. Десятая микросхема считается неисправной, если первые девять выдержали проверку.

Решение. ЕслиZслучайное число испытаний, то вероятность проведения каждого из них, гдеq = 1 – p. Вероятность десятого испытания.

Таким образом, вероятность каждого из десяти испытаний можно определить по табл.1.5.

Таблица 1.5. Ряд распределения числа испытаний

xi	1	2	3		9	10
	q	pq		...

Согласно определению математического ожидания имеем

Пример1.10. Ставятся 4 независимых опыта, в каждом из которых событиеА появляется с вероятностью 0,4. Рассмотрим случайную величинуZчисло появления событияАв четырех опытах. Построить ряд и функцию распределения случайной величиныZ. Найти ее математическое ожидание, дисперсию и среднее квадратичное отклонение.

Решение. Случайная величина Z может принимать значения {0,1,2,3,4}. Вероятность P(Z = z_i) вычисляется по формуле Бернулли:

.

В результате вычислений получим следующий ряд распределений (см. табл.1.6).

Таблица 1.6. Ряд распределения числа появления события А

	0	1	2	3	4
	1	4	6	4	1
	0,1296	0,3456	0,3456	0,1536	0,0256

Графики вариационного ряда и функции распределения вероятностей приведены на рис. 1.3 и 1.4.

Рис.1.3. Вариационный ряд Рис.1.4. Функция распределения

Математическое ожидание СВ Z, дисперсия и среднее квадратичное отклонение вычислим по формулам (1.21) – (1.29):

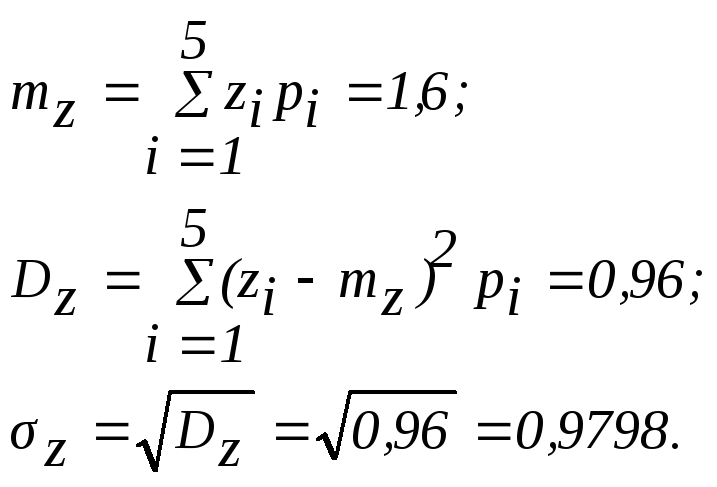
Пример1.11. В организации имеются 100 компьютеров. Вероятность безотказной работы каждого равна 0,98. Какова вероятность отказа двух компьютеров одновременно?

Решение. Отказ является событием, противоположным безотказной работе. Его вероятность для каждого компьютера

p=1–q=1–0,98= 0,02, n = 100.

Применим закон Пуассона

где = n ^. р = 100 ^. 0,02 = 2.

Тогда вероятность отказа двух компьютеров