Марченко_Высшая математика

Наибольшее и наименьшее значения функции на отрезке

Точки наибольшего и наименьшего значений функции на некотором множестве Х, в частности на отрезке, называются точками глобального, или абсолютного, экстремума этой функции на этом множестве.

Функция, непрерывная на отрезке [a; b], достигает своего наибольшего и наименьшего значений на этом отрезке либо в критических точках, принадлежащих отрезку, либо на его концах.

Например:

fнб

fнм

y			y
			fнб
			fнм
a	xmax b	x	a	xmin	b	x
min f (x)	= fнм		min f (x) = f (xmin ) = fнм
[a; b]			[a; b]
max f (x) = f (xmax ) = fнб			max f (x) = f (a)			= fнб
[a; b]			[a; b]

Правило нахождения наибольшего и наименьшего значений функции на отрезке [a; b]

1.Находим критические точки функции y = f (x), принадлежащие интервалу (a; b).

2.Вычисляем значения функции в критических точках и на концах отрезка.

3.Изполученныхзначенийвыбираемнаибольшееинаименьшее. Пример нахождения наибольшего и наименьшего значений

функции приведен в табл. 2.7.

Таблица 2.7

Пример нахождения наибольшего и наименьшего значений функции

Этапы

Функция y =

x3

, x

−2;

1

.

x −1

2

1. Находим и приравниваем к ну-

y′(x)

=

3x2 (x −1)− x3

=

x2 (2x −3)

;

лю производную y′(x)

(x −1)2

(x −1)2

x2 (2x −3) = 0 при x1 = 0 и x2 =

3

2

91

Окончание табл. 2.7

Этапы						Функция y =							x3	,	x	−2;		1	.
												x −1
																		2
2. Находим критические	точки,					Интервалу	−2;			1		принадлежит только
принадлежащие интервалу		−2;	1							2
						точка x1 = 0
			2
3. Вычисляем значения функции						y (0) = 0, y (−2) =					8		, y	1			1
в критической точке и на концах											3			= −			4
														2
отрезка
4. Из найденных значений выби-						yнб = y (−2) =	8								1		1
раем наибольшее и наименьшее									,	yнм = y						=−	4	,
							3
															2
						yнб − наибольшее значение, yнм − наи-
						меньшее значение функции на отрезке

Выпуклость и вогнутость функции. Точки перегиба

Функция y = f (x) называется выпуклой (вогнутой) на интервале (a; b), если любая дуга ее графика (отвечающего этому интервалу) расположена не выше (не ниже) стягивающей дугу хорды. Так, функция y = x2 выпукла, а y = −x2 вогнута на всей числовой оси.

Дифференцируемая функция выпукла (вогнута) на интервале, если ее график расположен не ниже (не выше) любой касательной к нему. Иногда для выпуклой (вогнутой) функции используется термин выпуклая вниз, вогнутая вверх (выпуклая вверх, вогнутая вниз).

Точки непрерывности функции, в которых меняется выпуклость на вогнутость или наоборот, называются точками перегиба функции. Если x0 − точка перегиба функции y = f (x), то точка (x0 ; f (x0 )) называется точкой перегиба графика этой функции. В окрестности точки перегиба график дифференцируемой функции лежит по разные стороны касательной к графику в точке перегиба.

Достаточные условия выпуклости и вогнутости функции

Если вторая производная f ′′(x)≥ 0 ( f ′′(x)≤ 0) во всех точках интервала (a; b), то функция y = f (x) выпукла (вогнута) на этом интервале. Если эти неравенства строгие, то и выпуклость (вогнутость) будет строгая.

92

y

y

f ′′(x) > 0

f ′′(x)< 0

0	a	b	x	0		a	b	x
Функция выпукла (строго)					Функция вогнута (строго)
Достаточные условия существования точек перегиба
Если вторая производная f ′′(x)					y	f ′′(x) > 0
при переходе через точку x0 , в ко-							f ′′(x)< 0
торой она равна нулю или не суще-						M
ствует, меняет знак и функция
непрерывна		в точке	x0 , то точка
x0 − точка перегиба функции, а точ-
ка М	(x0 ; f	(x0 )) − точка перегиба			0 a	x0	b	x
графика функции.

Схема исследования функции на выпуклость и отыскания точек перегиба

Схема следует из достаточных условий:

1)находим область определения функции y = f (x);

2)находим вторую производную f ′′(x) функции и точки из области определения, в которых вторая производная равна нулю

или не существует, отмечаем их на числовой прямой. Они разбивают область определения на интервалы, в которых f ′′(x) сохраняет знак;

3)определяем знак второй производной в каждом интервале

(для этого достаточно определить знак в какой-либо точке каждого интервала). Если в рассматриваемом интервале f ′′(x)< 0, то в этом интервале функция вогнута, если f ′′(x)> 0, то функция выпукла;

4)среди точек, в которых функция непрерывна, а вторая производная равна нулю или не существует, определяем те, при переходе через которые вторая производная меняет знак. Эти точки являются точками перегиба.

Пример исследования на выпуклость и точки перегиба представлен в табл. 2.8

93

Таблица 2.8

Пример исследования на выпуклость и точки перегиба

		Этапы			Функция y = x4			− 6x2
1. Находим		область	определения,	Функция определена, непрерывна и
промежуткинепрерывностифункции				дифференцируема для всех x (−∞; +∞)
2. Находим производную второго				y′ = 4x3 −12x; y′′ =12x2 −12 = 0					при
порядка	и	точки, в	которых она	x = −1 и x		=1
равна нулю или не существует				1	2
3–4. В каждом интервале, на кото-				Знак y′′(x)		+		−	+
рые точки x1 = −1 и x2			=1 разбивают	Характер			− 1		1
область	определения,		определяем
знак y′′(x)		и находим промежутки		функции		перегиб		перегиб
выпуклости и вогнутости функции				Функция:
				а) выпукла при x (−∞; −1) (1; +∞);
				б) вогнута при x (−1; +1);					x1 = –1 и
				в) точки	перегиба		функции
				x2 = 1;	перегиба		графика		функции
				г) точки
				(−1; −5)	и (1; −5)

Асимптоты графика функции

Под асимптотой кривой понимают прямую, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Различают асимптоты вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.

Прямая x = a называется вертикальной асимптотой гра-

фика функции y = f (x), если хотя бы один из односторонних пределов в точке x = a равен плюс (или минус) бесконечности, т. е.

lim f (x) = +∞(−∞) или

lim

f (x) = +∞(−∞).

x→a+0

x→a−0

Прямая y = kx + b называется наклонной асимптотой графика

функции y = f (x), если

lim

( f (x)− kx − b)= 0 , что равносильно

x→±∞

f (x)

существованиюконечныхпределов k = lim

,

b = lim

(

f

(

x

)

−kx

.

x→±∞

x

x→±∞

)

Запись x → ±∞ означает, что при

нахождении

наклонных

асимптот нужно отдельно рассматривать случаи x → +∞ и x → −∞. Если пределы различные, то график функции имеет более одной наклонной асимптоты.

94

Если k = 0, то b = lim f (x). Поэтому y = b − уравнение гори-

x→±∞

зонтальной асимптоты, т. е. горизонтальную асимптоту можно рассматривать как частный случай наклонной.

Примеры возможного расположения графика относительно вертикальной асимптоты

y

А

0

a

b

c

x

lim	f (x) = +∞	lim	f (x) = +∞	lim	f (x) = +∞
x→a−0		x→b−0		x→c−0
lim	f (x) = −∞	lim	f (x) = A	lim	f (x) = +∞
x→a+0		x→b+0		x→c+0

Прямые x = a и x = c − двусторонние вертикальные асимптоты, прямая x =b − левосторонняя асимптота.

Пример нахождения асимптот графика функции дан в табл. 2.9.

Таблица 2.9

Пример нахождения асимптот графика функции

Этапы

Функция

y

=

x2

+1

x

− 2

1. Находим область

определе-

Функция

определена

и

непрерывна при

ния и интервалы непрерывно-

x

−∞

(2;

+∞

), x

=

2

− точка разрыва

сти функции

(

; 2)

2. Определяем тип

точки раз-

lim

x2 +1

=

5

= −∞;

рыва, вычисляя односторонние

x − 2

−0

x→2−0

пределы. Если точка бесконеч-

x2 +1

5

ного разрыва, то существует

lim

=

= +∞;

вертикальная асимптота

x→2+0

x −2

+0

x = 2 − точка бесконечного разрыва;

прямая x = 2 – вертикальная асимптота

95

Окончание табл. 2.9

Этапы

Функция y

=

x2

+1

x

− 2

3. Находим наклонные y = kx +b

k =lim

f (x)

x2 +1

x2 +1

∞

асимптоты

графика функции.

=lim

=lim

=

=1;

x

(x −2)x

2

−2x

x→∞

x→∞

x→∞ x

∞

Строим эскиз

графика

функ-

(f (x)− kx)= lim

x

2

+1

ции в окрестности асимптот.

b = lim

− x

=

Замечание. Расположение гра-

x→∞

x→∞

x − 2

фика относительно наклонной

= lim

2x +1

∞

= 2;

асимптоты можно определить,

x − 2

=

сравнивая

значения ординаты

x→∞

∞

прямая

y = x + 2

− наклонная асимптота

для асимптоты и функции при

одних и тех же значениях абс-

при x → +∞ и x → −∞

циссы (достаточно больших):

y

x2 +1

=(x2 − 4)

+ 5 =

y = x+2

x − 2

x − 2

=(x + 2)+

5

> x + 2

при

x − 2

x > 2 . Значит, график функции

лежит выше асимптоты. При

0

2

x

x < 2 график функции

лежит

ниже асимптоты

Общая схема исследования функции и построения графика

Процесс исследования функции y = f (x) и построения графика можно условно разбить на следующие этапы:

1)предварительное исследование зависимости y = f (x);

2)исследование по первой производной;

3)исследование по второй производной;

4)построение схемы графика с учетом полученных результатов.

Целесообразно результаты исследования сопровождать

последовательным построением схемы графика.

Рассмотрим эти этапы подробнее. На 1-м этапе необходимо:

а) найти область определения функции и интервалы непрерывности;

б) если есть точки разрыва, найти односторонние пределы функции в этих точках и изобразить на чертеже поведение функции вблизи каждой точки разрыва;

96

в) исследоватьфункциюначетность, нечетность, периодичность; г) найти асимптоты графика функции; д) изучить поведение функции при стремлении аргумента к

граничным точкам области определения (если это не ясно из предыдущих исследований);

е) найти (если это возможно) точки пересечения графика с осями координат и отметить их на схеме графика.

На 2-м этапе необходимо:

а) найти первую производную f ′(x);

б) найти критические точки ( f ′(x) = 0 или не существует); в) найтиинтервалывозрастания( f ′(x) >0) иубывания( f ′(x) <0); г) найти точки максимума и минимума, вычислить значения

функции в этих точках; изобразить на чертеже поведение функции в окрестности каждой из этих точек.

На 3-м этапе необходимо:

а) найти вторую производную f ′′(x);

б) найти промежутки вогнутости		( f ′′(x) < 0) и выпуклости
( f ′′(x)	> 0);
в)	найти точки перегиба ( f ′′(x)=	0 или не существует, но

вокрестности точки меняет знак), вычислить значения функции

вэтих точках и изобразить поведение функции в окрестности этих точек на чертеже.

4-й этап предполагает построение схемы графика с использованием полученных данных.

Заметим, что приведенная схема исследования не является обязательной. При решении конкретной задачи отдельные этапы этой схемы могут быть расширены, другие же могут оказаться излишними или невыполнимыми, поэтому порядок пунктов схемы исследования может быть несколько нарушен. Так, в более простых случаях достаточно выполнить лишь несколько операций, например пункты а), е) первого этапа и пункт г) второго этапа. Если же график функции не совсем ясен и после выполнения всех этапов исследования, то можно построить дополнительно несколько точек графика, выяснить другие особенности функции.

Примеры исследования функции и построения графиков представлены в табл. 2.10 и 2.11.

97

Таблица 2.10

Пример исследования функции y = x3 − 6 x2 + 9 x + 3

и построения графика

Этапы

Функция

y = x3 − 6x2 + 9x + 3

1. а) найдем

область оп-

Так как функция является многочленом, то она

ределения и

интервалы

определена и непрерывна при всех

x \. Точек

непрерывности функции

разрыва нет

в) исследуем функцию на

Область определения симметрична относительно

четность, нечетность, пе-

начала координат и

y(−x) ≠ y(x), y(−x) ≠ −y(x),

риодичность

f (x +T ) ≠ f (x), x Df , T > 0 . Значит, функ-

ция не является ни четной, ни нечетной, ни пе-

риодической

г) найдем асимптоты гра-

Так как нет точек разрыва, то нет и вертикальных

фика функции

асимптот. Наклонные

асимптоты

отсутствуют

в силу того, что lim

f (x)

= +∞

x

x→∞

д) найдем пределы функ-

lim

x3 − 6x2

+ 9x + 3

)

= +∞;

ции при стремлении аргу-

x→+∞ (

мента к границам области

lim

x3 − 6x2

+ 9x + 3

)

= −∞

определения (x → ±∞)

x→−∞ (

е) найдем точки пересе-

Точка (0; 3)

− точка пересечения с

осью Оy

чения с осями координат

(при х = 0 у = 3). Положение точки пересечения

(какие возможно)

с осью Ох определится дальше

2. а)−г) найдем интерва-

y′ =3x2 −12x +9 =3

(

)(

)

1

2

x

−1

x

−3 =0 при x

=1; x =3;

лы возрастания и убыва-

max

min

ния, точки экстремума

Знак y′(x)

+

–

+

Поведение

1

3

x

функции

(−∞; 1) и (3; + ∞) – интервалы возрастания;

(1; 3) – интервал убывания функции;

x = 1 – точка максимума, x = 3 – точка минимума,

y (1) = 7, y (3) = 3

3. а)−в) найдем интерва-

y′′ = 6x −12 = 0 при x = 2,

y (2) = 5; y′′(x) < 0 при

лы выпуклости, вогнуто-

x < 2

(функция вогнута)

и y′′(x) > 0

при x > 2

сти, точки перегиба

(функция выпукла), значит, х = 2 – точка переги-

ба функции, а точка (2; 5) – точка перегиба гра-

фика функции

98

Окончание табл. 2.10

Этапы

Функция

y = x3 − 6x2 + 9x + 3

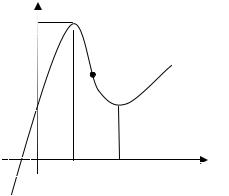
4. Построим

схематиче-

7

у

ский график функции.

Замечание. График функ-

ции пересекает ось

Ох

(2; 5)

в одной точке x = c,

при-

3

надлежащей

интервалу

(–1; 0). Значит, уравнение

x3 −6x2

+9x + 3 = 0 имеет

один действительный ко-

с

1

3

x

рень x = c

x2

Таблица 2.11

Пример исследования функции y =

и построения графика

x −1

Этапы

Функция

y =

x2

x −1

1. а) найдем область оп-

Функция определена и непрерывна при всех x ≠1

ределения

и

интервалы

(как частное двух непрерывных функций);

x =1 –

непрерывности функции

точка разрыва

б) исследуем

тип точки

x2

1

x2

1

разрыва x =1. Для этого

lim

=

= −∞; lim

=

= +∞.

x −

1

x −

1

x→1−0

−0

x→1+0

+0

найдем

односторонние

Так как в точке x =1 функция терпит бесконечный

пределы при x →1

разрыв,

то

прямая

x =1 является

вертикальной

асимптотой

г) найдем

наклонные

k = lim

f (x)

= lim

x2

= lim

x

=1,

асимптоты y = kx +b.

1

x→±∞

x

x

→±∞ x (x −1)

x

→±∞ x −

Замечание. Отличие сте-

( f (x)− kx)=

x

2

x

пени многочлена в чис-

b = lim

lim

− x

= lim

=1.

1

лителе от степени мно-

x→±∞

x→±∞ x −1

x→±∞ x −

гочлена

в

знаменателе

Прямая

y = x +1

−

наклонная

асимптота

при

на единицу

свидетель-

x → +∞ и x → −∞.

ствует о наличии на-

x2

(x2

−1)+1

1

клонной асимптоты

Так как

x −1 =

x −1

= (x +1)+ x −1 > x +1 при

x >1, то график функции расположен выше асим-

птоты, аналогично ниже асимптоты при x <1

в), е) исследуем функ-

Так как область определения не симметрична от-

цию на четность, най-

носительно нуля,

то функция не будет ни четной,

дем точки

пересечения

ни нечетной. При x = 0 y = 0, значит, график функ-

с осями

ции пройдет через начало координат

99

Окончание табл. 2.11

Этапы

Функция

y =

x2

x

−1

2. а)−г)

исследуем функ-

y′ =

2x (x −1)− x2

=

x

2 −

2x

,

y′ = 0,

x2 −2x = 0

цию на

экстремум

(x −1)

2

2

(x −1)

при

x1 = 0, x2 = 2.

Эти точки являются критиче-

скими. Исследуем знак производной в окрестности

каждой критической точки; y (0) = 0,

y (2) = 4.

Знак y′(x)

max

min

+

–

–

+

Поведение

х

функции

0

1

2

3. а)−в) найдем интерва-

y′′ =

2

≠ 0, значит,

точек перегиба нет;

при

лы выпуклости и вогну-

(x −1)3

тости, точки перегиба

x >1 функция выпукла (y′′ > 0) и при x <1 − во-

гнута (y′′ < 0)

4. Используя данные ис-

у

следования,

построим

схему графика функции.

4

Замечание.

Отдельные

y = x + 1

этапы исследования ино-

гда можно не проводить.

В данном случае точки

перегиба можно было не

находить, т. к. поведение

1

2

х

графикаопределялосьпре-

дыдущими

пунктами ис-

следования

2.2.2. Вопросы для самоконтроля

1. Что называется областью определения функции?

2. Как называется прямая x =a, если:

а) lim

f (x)= −∞ ; б) lim f

(x)= ∞?

x→a+0

x→a

3.Как найти вертикальные асимптоты графика функции?

4.Прямая y = b является горизонтальной асимптотой графика функции y = f (x) при x → +∞. Чему равен предел этой функции при x → +∞? Дать геометрическую иллюстрацию.

100