Марченко_Высшая математика

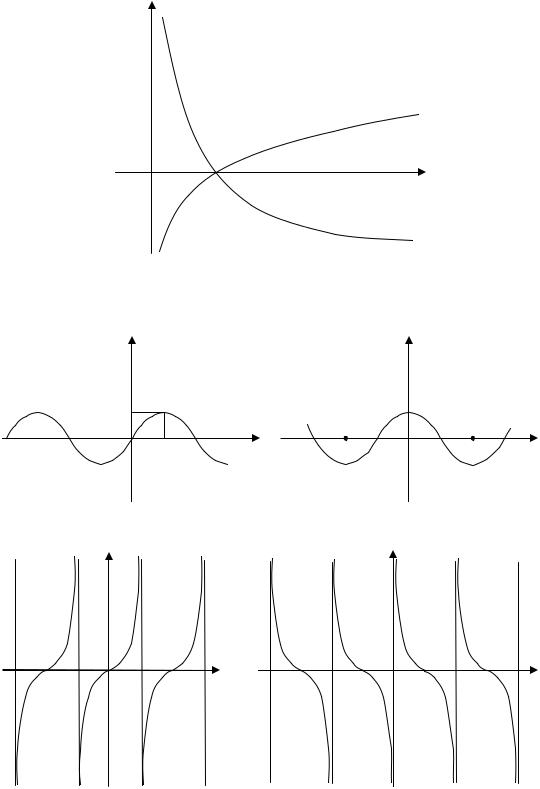
y = loga x, a > 1

y

0

1

x

	Рис. 1.11. График логарифмической функции
	y = sinx			y = cosx
	y			y
	1			1
–π	0	π π	x	–π –π 0	π π
		2		2	2
	y = tgx			y = ctgx
	y			y

	1			1
–π	0	π π	x	–π 0	π	π
2		2		2	2

Рис. 1.12. Графики тригонометрических функций

x

x

21

	y = arcsinx			y = arccosx
	y			y
	π			π
	2
				π
				2
–1	0			x
			1

–π	–1					x
		0		1
2
y = arctgx		y = arcctgx
y		π y

π

2

0

x

0

x

–π 2

Рис. 1.12. Графики обратных тригонометрических функций

Элементарными функциями называются все функции, которые можно получить из основных элементарных функций с помощью конечного числа арифметических действий (сложения, вычитания, умножения, деления) с применением действительных коэффициентов и образованием сложной функции.

Некоторые элементарные функции:

1)линейная функция y = ax + b;

2)квадратичная функция y = ax2 + bx + c;

3)многочлены с действительными коэффициентами (целые

рациональные функции) Pn (x) = an xn + an−1 xn−1 +... + a1 x + a0 ;

4) дробно-рациональные функции (рациональные дроби) –

отношение многочленов:

22

R(x)= Pn ((x)); Qm x

5) иррациональные функции – функции, в которых используется операция извлечения корня.

Некоторые неэлементарные функции:

1, x > 0,

1.y = sign x = 0, x = 0,−1, x < 0.

2.Дробная часть y ={x}= x −[x], где[x] означает целую часть x.

3.Функция Дирихле

1,	x − рациональное,
D(x)=	x −иррациональное.
0,

1.2. ТЕОРИЯ ПРЕДЕЛОВ 1.2.1. Теоретический минимум

1. Окрестность конечной и бесконечно удаленной точек.

2. Понятие предела функции. Односторонние пределы.

3. Бесконечно малые и бесконечно большие функции.

4. Основные теоремы о пределах.

5. Замечательные пределы.

6. Вычисление пределов.

7. Раскрытие некоторых видов неопределенностей.

Окрестность конечной и бесконечно удаленной точек

Окрестностью B(a) точки a (конечной точки) называется любой интервал, содержащий эту точку:

B(a)= (α; β) a.

ε-окрестностью			Bε (a)	точки а при ε > 0 называется интер-
вал вида (a −ε;		a + ε)	(рис. 1.13).
(	a	)	x	(	a	)
α		β		α – ε		α + ε x

Рис. 1.13. Окрестности точки a

23

Если из окрестности B(a)

или Bε (a) саму точку a

уда-

лить, то получим соответственно проколотую

ˆ

ˆ

(a) ок-

B(a)

или Bε

рестность этой точки.

ˆ

ˆ

B(x0 ) = (α; a) (a; β); Bε (a) = (a −ε; a) (a; a + ε).

Окрестность бесконечно удаленной точки:

B(

+∞) = (p; +∞) ={ x

: x > p},

p – любое действительное

число (рис. 1.14, а);

B(−∞)

= (−∞; q)={ x

: x < q},

q – любое действительное

число (рис. 1.14, б);

B(∞) = (−∞; q) (p; +∞), q < p – любые действительные числа

(рис. 1.14, в);

)

(

)

{

}

ε (

)

(

B

∞ =

−∞; −ε

+ε; +∞

=

x

:

x

>ε , где ε >0 (рис. 1.14, г).

p

x

q

x

а

б

q

p

x

–ε

+ε

x

в

г

Рис. 1.14. Окрестности бесконечно удаленной точки

Понятие предела функции. Односторонние пределы

Пусть функция y = f (x)

определена в некоторой проколотой

окрестности

ˆ

B(a) точки а.

y = f (x) при

Число b называется пределом функции

x → a,

если для любой окрестности B(b)

точки b найдется такая проко-

лотая окрестность

ˆ

точки

а,

что как

ˆ

(a), то

B (a)

только x B

f (x) B(b),

что

обозначается

b = lim f (x)

или

f (x)→ b при

x → a ( f (x)

x→a

стремится к b при x, стремящемся к а).

Коротко определение предела можно записать с помощью ло-

гической символики:

ˆ

ˆ

b = lim f (x) B(b) B

(a) (x B(a) f (x) B(b)).

x→a

Здесь точки а, b могут быть как конечные, так и бесконечные, что приводит к некоторым частным понятиям предела.

24

Примеры:

1) конечные пределы в конечной точке (a , b ). В этом случае в качестве окрестностей точек а и b можно взять δ- и ε-окрестности, и тогда определение предела удобно записывается на языке «ε − δ»:

b = lim f

(x) ε > 0 δ = δε > 0 (0 <

x − a

< δ

f (x)−b

< ε).

x→a

Таким

образом,

число b называется пределом функции

y = f (x) при x → a,

если для любого как угодно малого ε > 0

найдется такое число δ > 0, что для всех х, удовлетворяющих условию x − a < δ, x ≠ a, будет выполняться неравенство f (x)−b < ε

(рис. 1.15).

y

y = f (x)

b + ε

b

b – ε

0		a – δ a a + δ					x
		Рис. 1.15. Выбор окрестности точки а
		по заданной ε-окрестности точки b
2) конечные пределы на бесконечности (b					). В частности,
	b = lim f	(x) ε > 0 δ = δε > 0 (x > δ		f	(x)−b		< ε).
	x→+∞

25

Таким образом, число	b называется	пределом функции
y = f (x) при x →+∞, если	для любого	как угодно малого

ε > 0 найдется такое число δ > 0, что для всех х, удовлетворяющих условию x > δ, будет выполняться неравенство f (x)−b < ε

(рис. 1.16).

y	y
b + ε	b + ε
b	b
b – ε	b – ε

0 δ

x

0

δ

x

Рис. 1.16. Выбор окрестности бесконечно удаленной точки по заданной ε-окрестности точки b

Остальные частные случаи пределов запишем в сжатой форме с помощью логической символики:

b = lim f (x) ε < 0 δ = δε > 0 (x < δ

f

(x)−b

< ε);

x→−∞

b = lim f (x) ε > 0 δ = δε > 0 (

x

> δ

f

(x)−b

< ε).

x→∞

3) бесконечные пределы в конечной точке

(a ). В этом

случае в качестве окрестности точки а можно взять δ-окрестность. В частности,

lim f (x)= +∞ M > 0 δ = δM > 0 (0 < x − a < δ f (x)> M ).

x→a

Таким образом, функция y = f (x) при x → a имеет предел, равный +∞, если для любого как угодно большого M > 0 найдется такое число δ > 0, что для всех х, удовлетворяющих условию x − a < δ, x ≠ a, будет выполняться неравенство f (x)> M

(рис. 1.17).

26

y

M

0	a – δ	a a + δ	x
	Рис. 1.17. Предел, равный +∞

Остальные частные случаи пределов запишем в сжатой форме с помощью логической символики:

lim f (x)= −∞ M < 0 δ = δM > 0 (0 < x − a < δ f (x)< M );

x→a

lim f (x)= ∞ M > 0 δ = δM > 0 (0 < x − a < δ f (x) > M ).

x→a

4) бесконечные пределы на бесконечности запишем в сжатой форме с помощью логической символики:

lim f (x)= +∞ ε > 0 δ = δε > 0 (x > δ f (x)> ε);

x→+∞

lim f (x)= −∞ ε < 0 δ = δε > 0 (x > δ f (x)< ε);

x→+∞

lim f (x)= −∞ ε < 0 δ = δε < 0 (x < δ f (x)< ε);

x→−∞

lim f (x)= +∞ ε > 0 δ = δε < 0 (x < δ f (x)> ε);

x→−∞

lim f (x)= ∞ ε > 0 δ = δε > 0 (x > δ f (x) > ε).

x→∞

Важным частным случаем понятия предела функции является понятие предела последовательности.

27

Конечное число а называется пределом числовой последова-
тельности {x	}, если для любого сколь угодно малого положи-
n	ε найдется такое натуральное число n0 (ε), что все
тельного числа
члены этой последовательности с номерами n > n								(ε) удовлетво-
ряют неравенству			x	− a		< ε.	0
В этом случае			n				или x →a	(при n → +∞)
				пишут lim x = a
						n→∞ n	n
и говорят, что последовательность {x }							(или переменная x ) имеет
						n		n

предел а.

Для случая последовательности часто вместо n →+∞ пишут n → ∞. Таким образом,

a = lim xn ε > 0 n0 (ε)( n > n0 (ε) xn − a < ε).

n→∞

Говорят, чточисловаяпоследовательность{xn}стремитсяк +∞ (аналогично к −∞), что записывается xn →+∞ (соответственно xn →−∞), если для любого наперед заданного как угодно большого положительного числа М найдется такое натуральное число n0 = n0 (M ), что для всех n > n0 члены этой последовательности удовлетворяют неравенству xn > M (соответственно xn < −M).

Так, при xn →+∞ можно записать:

lim xn = +∞ M > 0 n0 (M )( n > n0 (M ) xn > M ).

n→∞

Отметим, что для существования предела функции при x → a не требуется, чтобы функция была определена в точке а. При нахождении предела рассматриваются значения функции в точках из окрестности точки а, отличные от а.

Поясним это на примере.

	Пример. Рассмотрим функцию f (x)=				x2 + x −6	. При x = 2 она
					x − 2
		x2	+ x − 6
	не определена. Покажем, что lim			= 5. Для этого достаточно
			x − 2
	x→2

для любого ε > 0 найти такое δ > 0, что для всех х, удовлетворяющих

условию

x − 2

< δ,

будет выполняться неравенство

f (x)−5

< ε.

Имеем

f (x)−5

=

(x +3)(x − 2) −5

=

(x + 3)−5

=

x

− 2

< ε. Возь-

x − 2

f (x)−5

мем δ = ε, тогда для

x − 2

< ε выполняется неравенство

< ε.

28

Односторонние пределы

Если значения функции y = f (x) стремятся к b1 при x → a, причем х принимает только значения меньше а, то записывают

lim f (x)= b1 и b1 называют пределом слева в точке а. Если х

x→a−0

принимает только значения больше а, то записывают lim f (x)=b2

x→a+0

и b2 называют пределом справа в точке а.

	b1	= lim		ˆ	ˆ
			f (x) B(b1 ) B(a)(x B(a), x < a f (x) B(b1 ));
		x→a−0
	b2	= lim		ˆ	ˆ
			f (x) B(b2 ) B(a)(x B(a), x > a f (x) B(b2 )).
		x→a+0
		Значения односторонних пределов обычно записывают сле-
дующим			образом: предел слева		– lim f (x)= f (a − 0), предел
				f (x)= f (a + 0).	x→a−0
справа – lim
		x→a+0
		Бесконечно малые и бесконечно большие функции
		Функция		y = α(x) называется бесконечно малой (бмф) при
x → a, если				lim α(x)= 0 (т. е. для любого сколь угодно малого
				x→a

ε > 0 найдется такая проколотая окрестность точки а, что для всех х из этой окрестности справедливо неравенство α(x) < ε).

			Пример.			Функция y = 4 − x			является бмф при	x → 4 , т. к.
	lim	(4		− x)= 0		, а функция	y =	1	является бмф при	x → ∞, т. к.
								x2
	x→ 4	1
	lim				= 0 .
	x→∞ x2

Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции

Сравнение бесконечно малых функций производится путем нахождения предела их отношения. Пусть α(x) и β(x) – бмф при

x → a, причем

β(x)

lim ( ) = A.

x→a α x

29

Тогда если:

1)А = 1, то α(x) и β(x) называются эквивалентными бмф

при x → a, что записывается в виде α(x) ~ β(x);

2)A ≠ 0 и A ≠ ∞, то α(x) и β(x) – бмф одного порядка ма-

лости при x → a;

3)A = 0 , то β(x) есть бмф более высокого порядка малости,

чем α(x), при x → a, что записывается в виде β(x) = o(α(x));

4)A =∞, то α(x) есть бмф более высокого порядка малости,

чем β(x), при x → a, что записывается в виде α(x) = o(β(x)).

Свойства бесконечно малых функций

1.

Алгебраическая сумма конечного числа бесконечно малых

функций есть бмф.

2.

Произведение бесконечно малой функции на ограниченную

функцию есть бмф.

3.

Если α(x) ~ β(x), то β(x) ~ α(x).

4.

Если α(x) ~ β(x) и β(x) ~ γ(x), то α(x) ~ γ(x).

5.

Если α(x) ~ β(x), то α(x)−β(x)= o(α(x))= o(β(x)).

6.

Если α(x) ~ α′(x) и β(x) ~ β′(x), то lim

β(x)

= lim

β′(x)

.

x→ a

α(x)

x→a

α′(x)

Следует отметить, что частное от деления бмф не обязательно

бесконечно малая функция.

Пример. Рассмотрим функции α(x)= 1 , β(x)=

1

, γ(x)=

1

+

1

.

x2

x

x

x2

Тогда α(x) – бмф при x → ∞, β(x) – бмф при x → ∞, γ(x)

– бмф

при x → ∞.

α(x)

= x есть функция бесконечно большая при x

Частное

→∞;

β(x)

частное

β(x) 1

есть бмф при x → ∞; частное

γ(x)

1

есть

= x

=1 + x

α(x)

α(x)

функция, имеющая конечный предел при x → ∞.

Функция y =β(x) называется бесконечно большой (ббф) при

x → a, если limβ(x)= ∞ или lim

β(x)

= +∞.

x→a

x→a

30