Марченко_Высшая математика

Найти точки разрыва, определить их тип и сделать схематический чертеж следующих функций:

	10 − x, если x < 2,
15.											если x = 2,
	f (x) = 3,
			3	,							если x > 2.
	x
			2			− 4, если x < −3,
	x
17.	f (x) = 5,										если x = −3,
			− x,								если x > −3.
	2
	−1,										если x <1,
19.			− 2,								если x =1,
	f (x) = x
					2		,				если x >1.
	3x
	x + 4									,	если x < 4,
				x
21.											если x = 4,
	f (x) = −1
			x,								если x > 4.
	ex ,										если x ≤ 0,
23.			− x,								если 0 < x ≤1,
	f (x) = 1
			1
	x −1, если x >1.
	−1,										если x < 0,
25.
	f (x) = cos x, если 0 ≤ x ≤ π,
			− x,								если x > π.
	1

			2	,	если x <1,
	x
16.	f (x) = 3,				если x =1,
					если x >1.
	x,
			2	− 2, если x < −3,
	x
18.	f (x) = 7,					если x = −3,
			− x,			если x > −3.
	4
	x − 2,					если x <1,
20.						если x =1,
	f (x) = −1,
				2	,	если x >1.
	3x
		1 − x, если x ≤0,
22.						если 0 < x ≤ 2,
	f (x) = 0,
	x −3, если x > 2.
	2,					если x < −1,
24.			− x,			если −1 ≤ x ≤1,
	f (x) = 1
						если x >1.
	ln x,
	3,					еслиx <−1,
26.		− x,				если −1≤ x ≤1,
	f (x) = 2
		+ln x, еслиx >1.
	3

Минимум для аудиторной работы

Исследовать на непрерывность в указанных точках следующие функции: 1; 7; 9; 12.

Найти точки разрыва, определить их тип и сделать схематический чертеж следующих функций: 15; 17; 19; 21.

61

1.3.4.Ответы

1.x1 = −1 – точка бесконечного разрыва; x2 =3 – точка непрерывности функции. 2. x1 = 2 – точка бесконечного разрыва; x2 =3 – точка непрерывности функции. 3. x1 = −3 – точка непрерывности функции; x2 = 2 – точка бесконечного разрыва. 4. x1 = 0 – точка

непрерывности функции; x2 =1 – точка бесконечного разрыва. 5. x1 = 2 – точка непрерывности функции; x2 =1 – точка бесконечного разрыва. 6. x1 = 5 – точка непрерывности функции; x2 = 4 – точка бесконечного разрыва. 7. x1 = 0 – точка непрерывности функции; x2 =1 – точка устранимого разрыва. 8. x1 = 0 – точка непрерывности функции; x2 =1 – точка конечного разрыва. 9. x1 = 0 – точка непрерывности функции; x2 = −1 – точка бесконечного разрыва. 10. x1 = 0 – точка бесконечного разрыва; x2 = −1 – точка непрерывности функции. 11. x1 = 2 – точка непрерывности функции; x2 =1 – точка конечного разрыва. 12. x1 = −1 – точка устранимого разрыва; x2 =1 – точка непрерывности функции. 13. x1 = −2 – точка непрерывности функции; x2 = 2 – точка устранимого разрыва. 14. x1 =1 – точка устранимого разрыва; x2 = 2 – точка непрерывно-

сти функции. 15. x = 2 – точка устранимого разрыва. 16. x =1 – точка устранимого разрыва. 17. Функция не имеет точек разрыва. 18. Функция не имеет точек разрыва. 19. x =1 – точка конечного разрыва. 20. x =1 – точка конечного разрыва. 21. x1 = 0 – точка

бесконечного разрыва; x2 = 4 – точка устранимого разрыва. 22. x1 = 0 – точка конечного разрыва; x2 = 2 – точка конечного разрыва. 23. x1 = 0 – точка непрерывности функции; x2 =1 – точка

бесконечного разрыва. 24. Функция не имеет точек разрыва. 25. x1 = 0 – точка конечного разрыва; x2 = π – точка конечного

разрыва. 26. x1 = −1 – точка непрерывности функции; x2 =1 – точка конечного разрыва.

62

Глава 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ И ЕГО ПРИЛОЖЕНИЯ

2.1. ОСНОВНЫЕ ПОНЯТИЯ

ÈТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ

2.1.1.Теоретический минимум

1.Определение производной. Дифференцируемость функции.

2.Техника дифференцирования.

3.Производные функций, заданных параметрически.

4.Производные функций, заданных неявно.

5.Логарифмическое дифференцирование.

6.Геометрический и физический смысл производной.

7.Дифференциал функции.

8.Теоремы о дифференцируемых функциях.

9.Правило Лопиталя.

Определение производной. Дифференцируемость функции

Пусть		функция y = f (x) определена на некотором интерва-
ле (a;	b).	Выберем точку x0 (a; b). Выберем другую точку
x = x0 +	x (a; b). Величина x = x − x0 называется прираще-

нием аргумента. Найдем соответствующее приращение функции

y= f (x0 + x) – f (x0 ) = f (x) − f (x0 ).

Производной функции y = f (x) вточке x0 называется предел от-

ношения приращения функции y = f (x0 +

x) – f (x0 ) к приращению

аргумента x при

x → 0, если этот предел существует и конечен:

f ′(x0 )= lim

y

= lim

f

(x0 + x)− f (x0 )

= lim

f

(x)− f

(x0 )

.

x

x

x − x0

x→0

x→0

x→x0

Производная

f ′(x ) существует, если существуют и равны

0

f ′(x )

= f ′(x

),

конечные односторонние производные в точке x0:

f (x)− f (x0 )

+

0

−

0

где f+′(x0 )=

lim

– правосторонняя

производная,

x − x

x→x0

+0

f−′(x0 )= lim

f (x)− f (x0 )

0– левосторонняя производная.

x − x0

x→x0 −0

63

	Если для некоторого значения x0 выполняется одно из условий:
lim	y = +∞ или lim		y = −∞, то в точке x0 существует бесконеч-
x→0	x	x→0	x
ная производная, равная соответственно +∞, –∞.
	Для обозначения производной функции y = f (x) используют
символы: y′,		f ′(x), y′x , dy ,		df (x)	.
			dx	dx

Схема нахождения производной представлена в табл. 2.1.

Таблица 2.1

Схема нахождения производной функции по определению

Этапы

Пример для функции f (x) = 2x − 7x2

1. Придать фиксированному зна-

f

(x0 +

x) = 2(x0 +

x)− 7 (x0 + x)2

чению x0 D (x) приращение x

и

вычислить

значение

функции

f

(x0 +

x)

2. Найти

приращение

функции

y = 2(x0 +

x)− 7 (x0 +

x)2 −

y = f (x0 + x) – f (x0 )

−

(2x0 − 7x02 )= 2x0 + 2 x−7x02 −14x0 x −

−7 ( x)2 −2x0 +7x02 = 2 x −14x0 x − 7 ( x)2

3. Составить отношение

y

y = 2

x −14x0 x − 7 (

x)2

=

x

x

х

=

x (2 −14x0 − 7 x)

= 2

−14x − 7 x

х

0

4. Найти lim

y

= y′

y′ = lim

(

2 −

14x − 7

x

)

= 2

−14x

x

x→0

0

0

x→0

Функция, имеющая производную в точке, называется дифференцируемой в этой точке, а операция нахождения производной называется дифференцированием.

Функция, имеющая конечную производную в каждой точке данного промежутка, называется дифференцируемой в этом промежутке.

Связь дифференцируемости и непрерывности функции

Если функция дифференцируема в данной точке, то она непрерывна в ней.

Обратное утверждение неверно, т. е. если функция непрерывна в точке, то она может быть не дифференцируемой в этой точке.

64

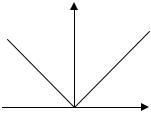
Например, функция

y =

x

x,

x ≥ 0,

=

−x, x < 0

непрерывна, но не дифференцируема в точке x = 0.

В точке x = 0 имеем:

y =

x

y =

f (0 +

x)− f (0)

f ( x)

x

=

=

.

x

x

x

x

Односторонние пределы не равны меж-

ду собой, т. к. при

x → 0

lim

y = −

x = −1,

lim

y

=

x

=1.

0

x

x

x→−0 x

x

x→+0

x

( x<0)

( x>0)

Следовательно, производная в точке x = 0 не существует.

Техника дифференцирования

Основные правила дифференцирования

Пусть u =u (x) и v =v(x) – дифференцируемые функции независимой переменной x; c = const. Тогда:

1. (c)′ = 0; (x)′ =1.

2. (u ± v)′ = u′± v′.

′

′

u

′

′

′

3. (u v)

′

′

; (cu)

′

u v −uv

v

= v

(

x

)

≠ 0

.

4.

=

2

, где

.

= u v +uv

= cu

v

v

Производная сложной функции

y = y(u(x)), где y = y(u),

Рассмотрим сложную функцию вида

u =u (x).

Если функция u =u (x) дифференцируема в точке x0 и функция

y =y(u) дифференцируема в точке u0 =u(x0 ), то функция y=y(u(x))

дифференцируема в точке x0 и

y′x (x0 )= yu′ (u0 ) u′x (x0 )

или символически y′x = yu′

u′x .

Производная обратной функции

Пусть функция y = y(x)

непрерывна, строго монотонна на ин-

тервале (a; b) и в точке x0 (a; b) имеет конечную и неравную ну-

лю производную. Тогда для обратной функции x =x(y)

в соответ-

ствующей точке y0

= y(x0 ) также существует производная, равная

x′y

=

1

.

y′x

65

Таблица производных

α ′

α−1

′

′

1

′

1.

(u

)

= αu

u , α = const,

u = u(x).

2. (

u )

=

u .

2

u

1

′

1

u ′

u

3.

= −

u′.

4. (a

)

= a

(ln a)u′.

u

2

u

6. (loga u)′ =

1

u′.

5.

(eu )′ = euu′.

u ln a

′

1

8. (sin u)′ = cosu u′.

7.

(ln u)

= u u′.

1

10. (cosu)′

= −sin u u′.

′

9.

(arcsin u)

=

u

′

.

12. (tgu)′ =

1

u′.

1 −u2

2

u

′

1

cos

′

′

1

11. (arccosu) = −

u

.

1 −u2

14. (ctgu)

= −

u′.

sin2 u

′

1

′

1

13. (arctgu)

=

u′.

15. (arcctgu) = −

u′.

1+u2

1+u2

Производные высших порядков

y = f (x)

Производной второго порядка функции

называется

производная от производной f ′(x) (обозначается

f ′′(x)

, d 2 y ):

dx2

f ′′(x)=(f ′(x))′.

Производной n-го порядка называется производная от производной (n–1)-го порядка:

f (n) (x)= (f (n−1) (x))′, n =1, 2, ...; f (0) = f (x).

Пример 1. Найти производные первого порядка функций:

1)	y =	4	+ 5	7x − 2;	2)	y = cos2 x sin x ;
		x2
3)	y = arctg x			;	4)	y = sin (ln 5x).
		1 + x2

Решение.

1) применим формулу производной суммы:

66

′

′

′

′

1

′

4

4

′

−

y′ =

+ 5

7 x − 2

=

+ (5 7 x ) − (2)

=

4(x

2 )

+ 5

7

x5

− 0 =

x

2

x

2

−4

8

7

8

7

= 4 (−2)x−3 + 5 7

1 x 5

= −

+

5

= −

+

1 5

;

x3

5 5

x3

5

x4

5 x4

2) применим формулу производной произведения, затем формулы (1), (8), (10) таблицы производных:

y

′

= (cos

2

′

2

x, v

= sin x,

′

′

′

=

x sin x) =

u = cos

(uv)

= u v

+ uv

= (cos

′

′

′

= (u

′

2

sin x + cos

2

2

2

′

=

x)

x (sin x)

= (cos

x)

) = 2u u , u = cos x

= 2cos x (cos x)′ sin x + cos2 x cos x = 2 cos x (−sin x) sin x + cos3 x =

=−2 cos xsin 2 x + cos3 x = cos3 x − 2 cos xsin2 x;

3)применим формулу производной частного и формулы (1), (13) таблицы производных:

			′
arctg x				= u = arctg x,
y′ =	1 + x	2

= (arctg x)′ (1 + x2 )− arctg x

(1 + x2 )2

2

u

′

′

′

v =1 + x

,

=

u v − uv

=

v

2

v

1

(1 + x2 )′

(1 + x2 )− arctg x (0 + 2x)

=

1 + x2

=

(

+ x2

)

2

1

= 1 − 2x arctg x

(1 + x2 )2 ;

4) используем формулы (7), (8) таблицы производных:

y′ = (sin (ln 5x))′ = (sin u )′ = cos u u′, u = ln 5x = cos (ln 5x)(ln 5x)′ =

′

1

′

1

′

1

cos(ln 5x)

=

(ln u)

=

u , u = 5x

= cos(ln5x)

(5x) = cos(ln 5x)

5

=

u

5x

5x

x

Пример 2. Найти производные указанного порядка:

1)

y = xex , y′′′(x);

2)

y = ln (cos x), y′′(x).

Решение.

1) y′ = (xex )′ = (x)′ex + x (ex )′ = ex + xex = ex (x +1),

y′′ = (ex (x +1))′ = (ex )′(x +1)+ ex (x +1)′ = ex (x +1)+ ex = ex (x + 2), y′′′ = (ex (x + 2))′ = ex (x + 2)+ ex = ex (x + 3);

67

′

1

′

−sin x

2) y′ = (ln (cos x))

=

(cos x)

=

= −tg x,

cos x

cos x

′

1

y

′′

= (−tg x)

= − cos2 x .

Производные функций, заданных параметрически

Если функция задана параметрически: x = x(t ),

то производ-

ные y′x , y′′xx

вычисляются по формулам

y = y (t ),

y′

(y′x )′

y′x =

t

; y′′xx =

′ t .

′

xt

xt

Пример. Найти производные y′x

и y′xx′

функции x = a cos3 t ,

y = asin3 t.

Решение. Найдем xt′ =(acos3 t)′ =3acos2 t (cost)′ = −3acos2 t sin t.

′

3asin2 t cost

sin t

yt′ =(asin3 t) =3asin2 t cost. Тогда

y′x

=

= −

= −tgt.

−3acos

2

t sin t

cost

1

(y′ )′ =(−tgt)′ =

−1

−

1

2

t

, y′′xx =

cos

=

.

−3a cos2 t sin t

3a cos4 t sin t

cos2 t

x

t

Производные функций, заданных неявно

Схемы нахождения производных функций, заданных неявно, представлены в табл. 2.2 и 2.3.

						Таблица 2.2
	′		неявной функции F (x; y) = 0
Схема нахождения производной yx
Этапы	Пример для функции х4 y2					−5x + 3y3 = 7
1. Продифференцировать обе час-	(х4 y2 )′ −5(x)′x +3(y3 )′ =					(7)′;
ти равенства F (x; y) = 0 по пере-	(x4 )′		x		x
менной x, считая, что y = y (x)			y2 + x4 (y2 )′ −5 +3 3y2 y′x = 0;
					x
	4x3 y2 + x4 2 yyx′ −5 + 9 y2 yx′ = 0
2. Из получившегося в результате	4x3 y	2 + 2x4 yy′		−5 +9 y2 y′ = 0;
дифференцирования равенства вы-			x		x
	y′x (2x4 y +9 y2 )= 5 −4x3 y2 ;
разить yx′ через x и y			5 − 4x3 y2
	yx′ =
			2x4 y +9 y	2

68

Таблица 2.3

′′

Схема нахождения производной yxx неявной функции F (x; y) = 0

Этапы

Пример для функции 4x2 − y2

= 4

1. Найти yx′

8x −2 yy′x = 0;

y′x

=

8x

= 4

x

2 y

y

2. Найти

y′′ = (y′ )

′ , считая,

y′′

= 4

y − xy′

xx

x

x

xx

y2

что y = y (x)

3. В полученное

выражение

x

4x

2

подставить

уже

найденное

y − x

4

y −

y

y

значение

y

′, тем самым вы-

y′′

= 4

= 4

=

′′

x

x

y2

y2

разив yxx

через y и x

y2 − 4x2

16

2

2

= 4

= y

− 4x

= −4 = −

3 .

y

3

y

Воспользовались условием задачи

Логарифмическое дифференцирование

При

дифференцировании

степенно-показательных

функций

y = u (x)

v(x)

, а также функций вида

y =

ϕ1

(x)ϕ2

(x) ... ϕn (x)

и в не-

ψ

(x)ψ

2

(x)

... ψ

n

(x)

1

которых других случаях часто бывает эффективным метод логарифмического дифференцирования. Суть метода заключается в том, что функцию сначала логарифмируют, а затем дифференцируют. Схема логарифмического дифференцирования дана в табл. 2.4.

Таблица 2.4

Схема логарифмического дифференцирования

Схема логарифмического

Пример для функции

дифференцирования

y = (sin x)

cos x

для функции y = u (x)v(x)

1. Логарифмируем функцию:

ln y = ln (sin x)cos x = cos x ln (sin x)

ln y = ln u (x)v(x) = v (x)ln u (x)

2. Дифференцируем:

u′(x)

(ln y)′ = −sin x ln (sin x)+ cos

2

x

;

′

(ln y)

= v′(x)ln u (x)+v (x)

;

sin x

u (x)

y′

cos2 x

y′

u′(x)

= −sin x ln (sin x)+ sin x

′

y

y = v

(x)ln u (x)+ v (x) u (x)

69

Окончание табл. 2.4

Схема логарифмического

Пример для функции

дифференцирования

y = (sin x)

cos x

для функции y = u (x)v(x)

3. Выражаем

y′

из полученного соот-

y′ =

cos2 x

ношения:

−sin x ln (sin x)+

sin x

×

u′(x)

v(x)

×(sin x)

cos x

y′ = u (x)

v′(x)ln u (x)

+v (x)

u

(x)

Пример. Найти производную для функции y =

х4 5

6 − х3

.

3 5

(х+ 7)

Решение.

1. Логарифмируем функцию:

х

4

5

6

− х

3

= ln (x

)+ ln (

)− ln (

5 )−ln x + 7 =

4

5

3

6

ln y = ln

6 − x

3

5 (х+ 7)

= 4ln x + 15 ln (6 − x3 )− 16 ln 5 − 12 ln (x + 7).

y′

4

−3x2

1

.

2. Дифференцируем:

= x +

−

y

5

(

6 − x3 )

2

(x + 7)

′

4

−3x

2

1

х

4 5

6 − х

3

′

5(6 − x3 )−

3 5 (х+ 7).

3. Выражаем y : y

=

x

+

2(x +

7)

Геометрический и физический смысл производной

Геометрический смысл производной

Значение производной в точке x0 равно угловому коэффициенту касательной к графику функции y = f (x)

в точке M (x0 ; f (x0 )): f ′(x0 )= k = tg α.

y{	y
f (x0)	M
	α
	x0 x0+ x x

Уравнениекасательнойкграфикуфункции y = f (x) вточкеx0 y = f (x0 )+ f ′(x0 )(x − x0 ).

70