Марченко_Высшая математика

58. 1. 59. 4. 60. 8. 61.				9	. 62.	1.			63. 2 . 64. 18.		65.	7 . 66. 2.	67. e−3 .
3			25			8			3			2
3	69. e−14 .		e−4 .			4			72. e−4 .	73. e−3 .		15	75. e−6 .
68. e2 .		70.			71.							74. e 2 .
						e	3	.
76. e−10.	77. e−21 .	78.	e−5 .		79. e4 .				80. e−6 .	81. 0.	82. ∞ . 83. 3. 84. 0.

85.0. 86. 32 . 87. −∞. 88. 16 . 89. − 43 . 90. 4.

1.3.НЕПРЕРЫВНОСТЬ ФУНКЦИИ

1.3.1.Теоретический минимум

1.Непрерывность функции в точке. Свойства функций, непрерывных в точке.

2.Непрерывность функции на отрезке. Свойства функций, непрерывных на отрезке.

3.Точки разрыва функции и их классификация.

Непрерывность функции в точке. Свойства функций, непрерывных в точке

Пустьфункция y = f (x)определенавнекоторойокрестноститочки x0. Придадим аргументу x0 приращение x. Тогда функция y = f (x) получитприращение y = f (x)− f (x0 )= f (x0 + x)− f (x0 )(рис. 1.18).

y

y = f(x)

y0 + y

y

y0

x

0

x0

x0 + x

x

Рис. 1.18. Приращение функции

51

Функция y = f (x) называется непрерывной в точке x0 , если:

1)f (x) определена в точке x0 и некоторой ее окрестности;

2)lim f (x)= f (x0 ).

→x0

	Из второго	условия вытекает,		что lim f (x) существует
				x→x0
и	конечен.	Это	равносильно	существованию	предела
lim	( f (x)− f (x0 ))= lim		y = 0. Таким	образом, второе	условие
x→x0		x→x
			0

вопределении означает, что

x→0 y →0 ,

т. е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции (определение непрерывности на языке приращений).

Так как lim x = x0 , то условие 1) можно записать в виде

x→x0

lim f (x)= f

lim x

= f (x ).

x→x0

(x→x0

)

0

Это означает, что для непрерывной функции знаки предела и

функции можно переставлять.

y = x3

Пример.

Доказать,

что функция

непрерывна в любой

точке области определения, т. е. в любой точке x0 .

x0 и

Решение. Дадим аргументу x приращение

x в точке

найдем приращение функции

y:

y = f (x0 + x)− f (x0 )= (x0 + x)3 − x03 = x03 + 3x02 x + 3x0 (

x)2 +

+(

x)3 − x 3 = 3x2 x + 3x

( x)2

+ ( x)3 .

0

0

0

Следовательно,

lim

y = lim

(

3x2

x + 3x

(

x)2 + ( x)3

)

= 3x2

lim

x + 3x

lim (

x)2 +

x→0

0

0

0

x→0

0

x→0

+ lim ( x)3 = 3x2

x→0

0 + 3x

0 + 0 = 0 .

x→0

0

0

y = 0, а это и означает, что функция y = x3

Таким образом, lim

x→0

непрерывна в точке x0 .

Если функция y = f (x) определена в левосторонней (или пра-

восторонней) окрестности точки x0 и

lim

f (x)= f (x0 −0)= f (x0 )

x→x0 −0

52

(аналогично lim f (x) = f (x0 + 0) = f (x0 )), то функция y = f (x)

x→x0 +0

называется непрерывной в точке x0 слева (соответственно справа).

Таким образом, функция y = f (x) непрерывна в точке x0 тогда и только тогда, когда она непрерывна в ней слева и справа.

Отсюда получаем удобный на практике критерий (условия)

непрерывности.
f (x) непрерывна при x = x0		в том и только том случае, если:
1)	функция определена в точке x0 ;
2)	односторонние пределы	f (x0 − 0), f (x0 + 0) функции в

точке x0 существуют, равны между собой и равны значению

функции в этой точке: f (x0 − 0) = f (x0

+ 0) = f (x0 ).

Пример. Исследовать

на непрерывность

в точке x =1 сле-

дующие функции:

1)

y =

3

; 2)

x − 2,

если x <1,

3)

y = x

2

−5.

y =

x −1

x2 ,

если x ≥1;

Решение.

3

1) функция

y =

определена в окрестности точки x =1, но

x −1

в самой точке x =1 она не определена, следовательно, в этой точке она не является непрерывной (не выполнено первое условие не-

прерывности);
2) для	исследования на		непрерывность			воспользуемся
условиями	непрерывности.		В	точке		x =1	функция
x − 2,	если	x <1, определена		( f 1 =12	=1), т. е.		первое
y =	если	x ≥1		( )
x2 ,

условие непрерывности выполнено; второе условие также выпол-
няется: f (1 − 0)= lim	f (x)= lim	(x − 2)= −1;	f (1 + 0)= lim f (x)=
x→1−0	x→1−0		x→1+0

= lim x2 =1 = f (1); третье условие непрерывности не выполняется,

x→1−0

т. к. f (1 − 0)≠ f (1 + 0). Следовательно, данная функция не явля-

ется непрерывной в точке x =1, однако функция непрерывна в точке x =1 справа;

3) функция y = x2 −5 является непрерывной в точке x =1,

т. к. выполнены все три условия непрерывности: она определена в точке x =1 и ее окрестности; существуют односторонние

53

пределы	lim	f (x) = −4,			lim f (x) = −4 ; эти	пределы		равны
между	x→1−0	и	равны		x→1+0	в	точке	x =1:
	собой				значению функции
lim f (x) = lim		f (x) = f (1) = −4 .
x→1−0	x→1+0
Свойства функций, непрерывных в точке
1. Если функции f (x)					и g (x) непрерывны в точке x0			, то их
арифметические комбинации: f (x)± g (x), c f (x)							(с – постоян-
ная), f (x) g (x) и			f (x)	(при условии что g (x )≠ 0 ), также непре-
			g (x)		0

рывны в точке x0 .

2. Если функция u = ϕ(x) непрерывна в точке x0 , а функция

y = f (u) непрерывна в точке u0 = ϕ(x0 ), то сложная функция y = f (ϕ(x)) непрерывна в точке x0 .

Непрерывность функции на отрезке. Свойства функций, непрерывных на отрезке

Функция y = f (x) называется непрерывной на отрезке [a; b], если она непрерывна в каждой точке интервала (а; b), в точке a непрерывна справа, а в точке b непрерывна слева.

Свойства функций, непрерывных на отрезке

1. Основные элементарные функции непрерывны в области их определения.

2. Элементарные функции непрерывны на каждом из интервалов, целиком лежащих в области определения.

3. Если функция y = f (x) непрерывна на отрезке [a; b], то она ограничена на этом отрезке (первая теорема Вейерштрасса).

4. Если функция y = f (x) непрерывна на отрезке [a; b], то на этом отрезке она достигает своего наименьшего значения fнм и наибольшего значения fнб (вторая теорема Вейерштрасса) (рис. 1.19).

y

fнб	y = f (x)

fнм

0

a

b

x

Рис. 1.19. Наибольшее и наименьшее значения непрерывной на отрезке функции

54

x→x0

5. Если	функция	y = f (x) непрерывна на			отрезке [a; b] и
f (a) = A, f	(b) = B , то для любого числа С, заключенного между А
и B, найдется такая точка с [a;				b], что f (c) = C (теорема Коши
о промежуточном значении) (рис. 1.20).
	y
	B			y = f (x)
	C
	A
	0	a	c	b	x
	Рис. 1.20. Промежуточные значения
	непрерывной на отрезке функции
Точки разрыва функции и их классификация
Если для функции y = f (x),				определенной по крайней мере

в некоторой проколотой окрестности точки x0 , не выполняется хотя бы одно из условий критерия непрерывности, то точка называется

точкой разрыва функции.

Точкиразрывафункцииклассифицируются следующимобразом.

Точка x0 называется точкой:
1) устранимого разрыва функции y = f (x), если в этой точке
существуют односторонние конечные пределы f (x0 −0) и f (x0 +0),
они равны между собой: f (x0 − 0) = f (x0 + 0), но сама функция
y = f (x) не определена в точке x0 или определена, но ее значение
неравно одностороннимпределам: f (x0 − 0) = f (x0	+ 0) ≠ f (x0 );
2) конечного разрыва (скачка) функции y = f	(x), если в этой
точке существуют конечные односторонние пределы f (x0 − 0) и
f (x0 + 0), но они не равны между собой: f (x0	− 0) ≠ f (x0 + 0)
(рис. 1.22, точка x = 0 );

3)бесконечного разрыва (скачка) функции y = f (x), если в этой точке хотя бы один из односторонних пределов бесконечен

(рис. 1.23, точка x1 = −4 );

4)несуществования, если не существует lim f (x).1

55

Если в точке устранимого разрыва функцию доопределить или значение сделать равным односторонним пределам, то функция в этой точке станет непрерывной.

	Пример 1. Исследовать на непрерывность в точке x = 0 функ-
цию f (x)= sin x .
			x
	Решение. Здесь x0 = 0 –				точка разрыва: в этой точке функ-
ция		не определена,		существуют		односторонние	пределы
f (x		−	0)= f (−0)= lim sin x =1 и f (x			+ 0)= f (+0)= lim sin x =1,
0			x→−0	x	0	x→+0	x
равные между собой. Точка					x0 = 0 является точкой устранимого

разрыва. Если эту функцию доопределить в точке x = 0 , то полу-

	sin x		, если x ≠ 0,
ченная функция		x		станет в точке	x0 = 0
	f (x) =
		1,	если x = 0

непрерывной (см. рис. 1.21).

y

1

–3π –2π	–π	0	π	2π	3π	x
Рис. 1.21. График функции y =				sin x
				x
Пример 2. Найти точки разрыва и определить их тип для
x +1,	если x < 0,
	если 0 ≤ x < 2,
функции f (x) = x2 −1,
	если x ≥ 2.
5 − x,

Решение. Функция f (x) определена и непрерывна на интервалах (−∞; 0), (0; 2) и (2; +∞), т. к. на каждом из этих интервалов она задана элементарными функциями (свойство 2). Следовательно,

56

точками разрыва данной функции могут быть только те точки, в ко-

торых функция меняет свое аналитическое задание, т. е. точки x1 = 0
и x2 = 2. Найдем односторонние пределы функции в точке x1 = 0:
f (0 − 0) = lim	f (x) = lim	(x +1) =1,
x→0−0	x→0−0	(
f (0 + 0) = lim	f (x) = lim		x2	−1 = −1.
x→0+0	x→0+0			)

Таккакодносторонниепределысуществуютиконечны, нонеравнымеждусобой, тоточка x1 =0 является точкойконечногоразрыва.

Для точки x2 = 2 находим:

f (2 − 0) = lim	f (x) = lim		(x2	−1)= 3;
x→2−0		x→2−0
f (2 + 0) = lim	f (x)	= lim	(5 − x) = 3, f (2) = (5 − x)			x=2 = 3.
x→2+0		x→2+0		f (2 − 0)= f (2 + 0)= f (2). Следова-
Таким образом,		имеем

тельно, в точке x2 = 2 функция является непрерывной. График данной функции изображен на рис. 1.22.

y

	3
	1
–1	0	1	2	3	5	x
	–1

x +1, если x < 0,

Рис. 1.22. График функции f (x) = x2 −1, если 0 ≤ x < 2,

5 − x, если x ≥ 2

Пример 3. Найти точки разрыва функции и определить их тип:

−3x,		если x ≥ −1,
f (x)= x		, если x < −1.
x + 4

57

Решение. Функция f (x)				на интервалах			(−∞; − 4), (−4;−1) и
(−1; +∞) определена и непрерывна, т. к. она задана элементарными
функциями (свойство 2).
В точке x2 = −4 функция не определена,							значит, точка x2 = −4
является точкой разрыва. Определим ее тип:
f (−4 − 0)= lim	f (x)		= lim	x		= +∞;
				x +	4
x→−4−0	x		x→−4−0
f (−4 + 0)= lim			= −∞.
	x + 4
x→−4+0
Следовательно,		в точке x2 = −4 функция терпит бесконечный
разрыв.
В точке x1 = −1		функция меняет свое аналитическое задание,

следовательно, в этой точке возможен разрыв. Найдем односторонние пределы:

	f (−1 − 0)= lim		f (x)= lim	x	= −1	;
				x + 4
		x→−1−0	x→−1−0		3
	f (−1 + 0)=	lim	f (x)= lim	(−3x)= 3,		f (−1)= (−3x)		x=−1 = 3.
		x→−1+0	x→−1+0
	Так как	f (−1 − 0)≠ f (−1 + 0), то точка x1 = −1 является точ-

кой конечного разрыва (рис. 1.23).

y

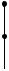3

		1
–4	–1
	0	1	x

	−3x, если x ≥ −1,
Рис. 1.23. График функции		x
	f (x) =		, если x < −1
	x + 4

58

Точки устранимого и конечного разрывов называют точками разрыва I рода.

Функция, которая на любом конечном интервале имеет конечное число разрывов I рода, называется кусочно-непрерывной

(на этом интервале).
Если хотя бы один из односторонних пределов f (x0 − 0) или
f (x0 + 0) не существует (рис. 1.24, точка x1 = 0 ) или равен беско-
нечности, то точки разрыва называют точками разрыва II рода.
Пример. Найти точки разрыва функции и определить их тип:
f (x)= sin 1 .
x	f (x)=sin 1 определена для всех значений x,
Решение. Функция
	x
за исключением x = 0 .	Точка x = 0 есть точка разрыва II	рода,
т. к. при x →0 как справа, так и слева значения функции		sin 1 ,
		x

колеблясь между –1 и +1, не приближаются ни к какому числовому значению. Другими словами, односторонние пределы не существуют.

y

1

–1	–1	0	1	1	x
π	2π		2π	π

–1

Рис. 1.24. График функции f (x) = sin 1x

59

1.3.2.Вопросы для самоконтроля

1.Что называется приращением функции y = f (x) в точке x0?

2.Дать определение непрерывности функции в точке x0.

3.Вчемсостоитсвязьмеждунепрерывностьюфункциивточкеx0

иее приращением в данной точке?

4.Дать определение непрерывной функции в точке x0 слева (справа).

5.Сформулировать критерий непрерывности в точке x0.

6.Сформулировать свойства функций, непрерывных в точке.

7.Сформулировать свойства функций, непрерывных на отрезке.

8.Какая точка называется точкой разрыва?

9.Какая точка называется точкой: устранимого, конечного, бесконечного разрыва?

10.Какие точки разрывов называют точками разрыва I рода?

11.Какие точки разрывов называют точками разрыва II рода?

1.3.3.Практический минимум

Исследовать на непрерывность в указанных точках следую-

щие функции:

1.

f (x) =

x +3

; x = −1, x = 3.

2. f (x) =

x +3

; x

= 2, x

= 3.

x +1

1

2

x − 2

1

2

3.

f (x) = 3x + 2

; x = −3, x = 2.

4. f (x) =

x + 2

; x

= 0, x

=1.

x2 −1

x2 − 4

1

2

1

2

1

1

5.

f (x) = 2

x−1

−1 ; x = 2, x =1.

6. f (x) = 2

−1 ; x =5, x = 4.

x−4

1

2

1

2

7.

f (x) =

x −1

; x = 0, x =1.

8.

f (x) =

x −1

; x

= 0, x

=1.

x2 −1

x −1

1

2

1

2

1

1

9.

f (x) = 2

x+1

;

x

= 0,

x

= −1.

10.

f (x) = 5x ;

x

= 0, x = −1.

1

2

1

2

11.

f (x) =

3

;

x

=2,

x =1.

12.

f (x) =

1+ x3

;

x

= −1,

x

=1.

1

1

2

1+ x

1

2

1+2x−1

13.

f (x) =

x2 −4

;

x

=−2, x =2.

14. f (x) =

x2 −4x +3

; x =1, x

=2.

x −2

1

2

x2 +3x −4

1

2

60