Лекции

2. Перестановки

8 января 2014 г. 0:00

Опр.

- все перестановки на множестве из элементов.

Свойства

группа:

Опр.

получается из транспозицией

Теорема
В группе	перестановок можно расположить так, чтобы каждая следующая

получалась из предыдущей с помощью одной транспозиции. Начинать можно с любой. доказательство (по индукции)

Б.И: n=2 (1,2) (2,1)

Ш.И:

Опр.

образует инверсию, если - число инверсий

Опр.

Перестановка называется чётной (нечётной), если количество инверсий в ней чётно (нечётно)

Теорема Транспозиция меняет чётность перестановки доказательство

1)

2)при перестановке не соседних элементов необходимо совершить нечётное количество перестановок соседних элементов.

Замеч.

Алгебра 1 Стр.41

3 и 4. Определение определителя порядка n. Определитель транспонированной матрицы. Свойства определителя матрицы.

10 января 2014 г.

18:30

Опр.

определителем матрицы А называется число из F, равное

Свойства

1)

2)

3)если в определителе есть нулевая строка, то определитель равен 0

4)Определитель матрицы с двумя одинаковыми строками равен 0

5)если есть две пропорциональные строки, то определитель равен 0

6)если к какой-либо строке прибавить другую, умноженную на число, то определитель не изменится

7)если в определителе строки поменять местами, то он изменит знак на противоположный

8)определитель транспонированной матрицы равен определителю исходной

Опр.
Минор	- определитель подматрицы М из матрицы А, из которой
взяты i-тые строки и j - тые столбцы.
Опр.
Дополнительный минор (к минору)		- то, что останется после

вычёркивания из матрицы строк и столбцов, на которых лежат элементы исходного минора.

Опр.

Алгебраическое дополнение (к минору)

Лемма
Пусть	, тогда произведение минора	на алгебраическое
дополнение	в определителе	является суммой
слагаемых этого определителя с нужными знаками.
доказательство
1. если угловой минор размера m
сумма индексов =		- чётна при

Алгебра 1 Стр.42

любом

m! перестановок

(n-m)! перестановок

перемножим: m!(n-m)!

перестановки записаны по порядку, значит имеет инверсию тогда и только тогда, когда имеет инверсию либо , либо

2.если минор взят не угловой, то нужно поменять строки и столбцы местами так, чтобы он стал угловым. При этом нужно учитывать смену знака на минус при

каждой смене строки или столбца. Теорема Лапласа

произведений всевозможных миноров, выбранных в зафиксированном m ( ) строках (столбцах) на алгебраические дополнения.

доказательство - число слагаемых в одном произведении минора на алгебраическое

дополнение.

есть n столбцов, сколько вариантов выбора m столбцов из n столбцов? итого

Следствие

m=1 - разложим по строке выбираем i-тую строку.

Алгебра 1 Стр.43

5. Определитель полураспавшейся матрицы

11 января 2014 г.

17:23

Опр.
Полураспавшаяся матрица - матрица	, у которой либо	, либо

Определитель такой матрицы

Алгебра 1 Стр.44

6. Определитель произведения матриц

11 января 2014 г.

17:24

Теорема определитель произведения матриц одного размера равен произведению определителей

доказательство

Алгебра 1 Стр.45

7. Обратимость матрицы, критерий обратимости

11 января 2014 г.

17:24

Опр.
Матрица	называется обратной к матрице , если	.
Теорема

- обратима доказательство

определитель единичной матрицы не может быть равным нулю. Формула нахождения обратной матрицы

, тогда

. является транспонированной матрицей

дополнений к числам исходной матрицы. Способ нахождения обратной матрицы №2

- элементарными преобразованиями довести это к тому, чтобы в левой части стояла , а в правой полученная обратная матрица.

Алгебра 1 Стр.46

8. Правило Крамера

11 января 2014 г.

21:44

Теорема Крамера

- система линейных уравнений, где A - квадратная матрица всех коеффициентов при неизвестных, а b - столбец значений, которые принимают уравнения.

Тогда система имеет одно решение, если , в противном случае она не имеет решений,

либо имеет бесконечно много решений. решение:

, где - это определитель матрицы, у которой i-тый столбец поменяли на

столбец b. доказательство

по определению обратной матрицы.

Алгебра 1 Стр.47

9. Комплексные числа. Матричная модель. Алгебраическая форма комплексного числа.

11 января 2014 г.

23:15

Опр. (матричная модель комплексного числа)

называется комплексным числом, множество комплексных чисел

обозначается

Теорема

- поле доказательство

-группа.

1.ассоциативность по сложению

2.существует нейтральный элемент

3.обратный элемент

4.коммутативность

-группа

1.ассоциативность

2.нейтральный элемент

3.обратный элемент существует

4.коммутативность

5.дистрибутивность (св. матриц)

Опр.

Опр. (алгебраическая формула комплексного числа)
, где	- действительная часть	- мнимая часть

Опр.

Пусть тогда - сопряжённое

Алгебра 1 Стр.48

Свойства сопряжённых чисел Пусть

1.

2.

3.

4.

5.

Алгебра 1 Стр.49

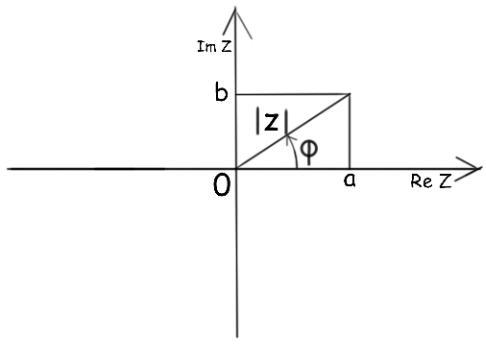
10. Тригонометрическая форма комплексного числа. Формула Муавра.

12 января 2014 г.

0:12

Опр.

Комплексная плоскость

- аргумент Z

Следствие

Формула Муавра если , то

Формула Эйлера

Алгебра 1 Стр.50