6.2. Алгебраический критерий устойчивости Гурвица

Пусть дано характеристическое уравнение системы вида

a₀ pⁿ + a₁ p^n-1 + a₂ p^n-2 + … + a_n-1 p + a_n = 0 при a₀ > 0. (6.2)

Гурвиц предложил алгебраический критерий, который основан на построении специальных определителей характеристического уравнения (6.2), называемых определителями Гурвица. Они составляются по следующим правилам:

1) по главной диагонали выписывают все коэффициенты от a₁доa_nв порядке возрастания индекса;

2) дополняют столбцы определителя вверх от диагонали с коэффициентами последовательно возрастающими, а вниз – с последовательно убывающими индексами;

3) на место коэффициентов, индексы которых большеnи меньше 0, ставят нули.

В соответствии с этими правилами, определитель Гурвицаn-го порядка для уравнения (6.2) имеет вид

. (6.3)

Определители Гурвица более низкого порядка являются диагональными минорами _n, например, приn = 3

₁ = a₁;;.

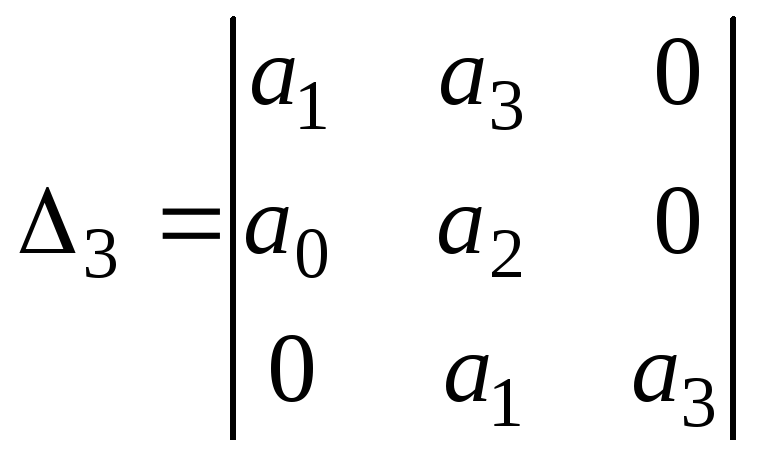Поскольку в последнем столбце определителя _nстоят нули, за исключениемa_n,то

_n = a_n_n–1. (6.4)

Критерий Гурвица формулируется следующим образом: для устойчивости АСУ необходимо и достаточно, чтобы все определители Гурвица ₁,₂, …,_nбыли положительными и при этом выполнялось условиеa₀> 0.

➢ Пример 12.1. Пусть АСУ описывается уравнением второго порядка, тогда характеристическое уравнение имеет вид

a₀ p² + a₁p + a₂ = 0,

а определитель Гурвица .

Условие устойчивости

a₀ > 0; ₁ = a₁ > 0; ₂ = a₂₁ = a₂ a₁ > 0.

Поскольку a₁> 0, должно выполняться условиеa₂> 0.

Таким образом, для устойчивости системы второго порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были положительными.

2. Пусть АСУ описывается ДУ третьего порядка, характеристическое уравнение которого имеет вид

a₀ p³ + a₁ p² + a₂ p + a₃ = 0,

а определитель Гурвица

.

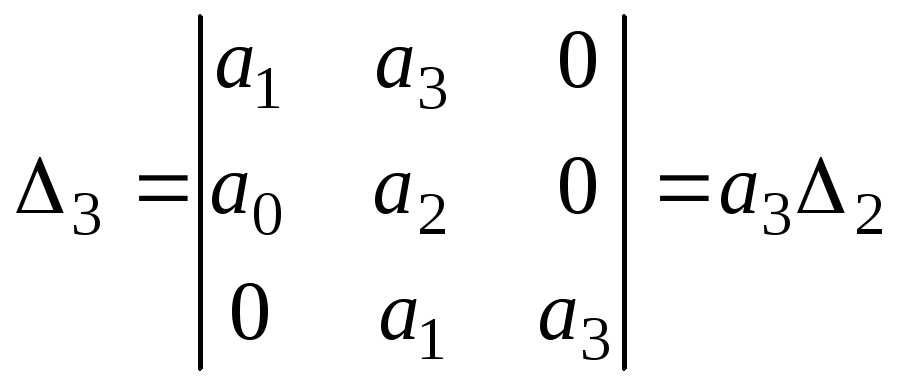Для устойчивой системы имеем

₃ = a₃ ₂ > 0; ;

₁ = a₁ > 0; a₀ > 0.

Следовательно, a₃> 0 иa₂> 0, т.е. условие положительности всех коэффициентов выдерживается. Кроме того, необходимо, чтобыa₁a₂>a₀a₃.

* * *

Таким образом, для уравнений выше второго порядка положительность всех коэффициентов является необходимым условием устойчивости АСУ. Но это условие не является достаточным, так как₂может не быть положительным при положительныхa₀,a₁,a₂,a₃. Условие₂> 0 позволяет в случае неустойчивой системы изменить ее параметры таким образом, чтобы она стала устойчивой.

Для характеристических уравнений высоких степеней (n> 5) анализ влияния коэффициентов на определитель Гурвица резко усложняется. Свободными от этого недостатка являются частотные критерии устойчивости.

6.3. Частотные критерии устойчивости

Эти критерии основаны на анализе расположения тех или иных частотных характеристик на плоскости. При этом достигается:

1) наглядность, так как задача исследования системы любого порядка сводится к изучению плоской кривой;

2) возможность экспериментального определения частотных характеристик системы, что позволяет исследовать такие системы, ДУ которых неизвестны;

3) сравнительно простой анализ влияния того или иного параметра на устойчивость, а также возможность суждения о качестве переходного процесса.

Частотные критерии можно разделить на две группы: первые предназначены для исследования замкнутой системы – критерий Михайлова (он применяется обычно для сложных систем); вторые – для исследования устойчивости замкнутой системы по частотной характеристике разомкнутой системы – критерий Найквиста (используется, когда размыкание системы приводит к существенным упрощениям частотной функции).

Критерий устойчивости Михайлова.Пусть дано уравнение замкнутой системыY(p) = W(p)X(p), гдеW(p) = В(p)/А(p) – передаточная функция замкнутой системы. Тогда ДУ системы, преобразованное по Лапласу,

A(p)Y(p) = B(p)X(p).

Характеристический полином этого уравнения имеет вид

A(p) = a₀ pⁿ + a₁ p^n – 1 + … + a_n – 1p + a_n.

В соответствии с основной теоремой алгебры этот полином можно разложить на множители:

A(p) = a₀(p – p₁)(p – p₂) … (p–p_n), (6.5)

где p₁, …,p_n– корни характеристического уравненияA(p) = 0.

Выражение(6.5)действительнопри любых значенияхp, в частности приp = j. Тогда (6.5) можно переписать так:

A(j) = a₀(j – p₁)(j – p₂) … (j–p_n). (6.6)

Выражение (6.6) называется кривой Михайлова и обычно обозначаетсяD(j) = = A(j). Каждый сомножитель выражения (6.6) отображается на комплексной плоскости вектором, конец которого лежит на мнимой оси (рис.6.4).

В основу критерия Михайлова положен принцип аргумента: произведение комплексных чисел имеет аргумент, равный сумме аргументов всех его сомножителей.

В нашем случае при изменении от –до+векторы сомножителей (j–p_i),поворачиваются на угол. Если корни лежат в левой части полуплоскости, то изменение угла будет положительным, если в правой, – то отрицательным (вектор (j–p_i) поворачивается против часовой стрелки в левой полуплоскости и по часовой стрелке – в правой).

Запишем выражение (6.6) в показательной форме. Учтем, что , где;.

Тогда

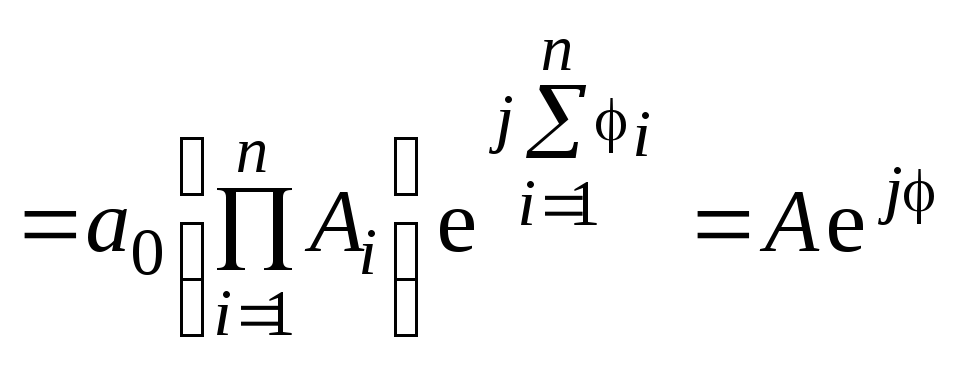. (6.7)

Из (6.7) вытекает, что изменение аргумента вектора Михайлова D(j) равно сумме изменений аргумента каждого сомножителя выражения (6.7), т.е. изменение аргумента

.

Если все корни характеристического уравнения расположены слева от мнимой оси (т.е. система устойчива), то изменение каждого из сомножителей равно +, а изменение аргумента произведения всех сомножителейargD(j) = +n.

Если хотя бы один корень будет расположен в правой полуплоскости (система неустойчива), то изменение аргумента вектора Михайлова argD(j) = +(n– 2).

Заметим, что при измененииот –до+кривая Михайлова симметрична относительно оси абсцисс, что позволяет ограничиться изучением кривой в диапазоне измененияот 0 до+.Тогда условие устойчивости системы по Михайлову можно записать в виде

. (6.8)

Годограф кривой Михайлова при изменении от 0 додляустойчивых систем при различных значениях n иллюстрирует рис.6.5.

В соответствии с (6.8) критерий Михайлова формулируется следующим образом: для того, чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при изменении от 0 довектор МихайловаD(j) повернулся на угол.

Рассматривая расположениеD(j) на комплексной плоскости, условие устойчивости можно сформулировать иначе: чтобы система была устойчива, необходимо и достаточно, чтобы годограф вектораD(j) прошел на комплексной плоскости последовательноn квадрантов в положительном направлении (против часовой стрелки), не проходя через начало координат. Если годограф проходит через начало координат, то система находится на границе устойчивости.

Расположение годографа на комплексной плоскости для различных систем иллюстрируетсярис.6.6.

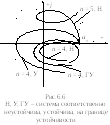
Критерий устойчивости Найквиста.Заметим, что частотная функция системW(j) на комплексной плоскости может бытьпредставлена как вектор и при непрерывномизмененииконец вектораW(j) будет скользить по некоторой кривой, представляющейграфическое изображениеАФЧХ системы (годограф вектора).

Имеем Y(p) = W(p)X(p), где– АФЧХ замкнутой системы;– АФЧХ разомкнутой системы.

Тогда [1 + W_p(p)]Y(p) = W_p(p)X(p), илиA(p)Y(p) = B(p)X(p).

Характеристическое уравнение замкнутой системы: 1 + + W_p(p) = 0 илиA_p(p) + B_p(p) = 0, гдеA_p(p) – характеристический полином разомкнутой системы.

В реальных системах степень полинома B_p(p) меньше степени полиномаA_p(p) вследствие инерционности динамических звеньев. Следовательно, полином {A_p(p) + B_p(p)} имеет ту же степень, что иA_p(p).

При p = j, разложив соответствующие полиномы на множители, имеем

,

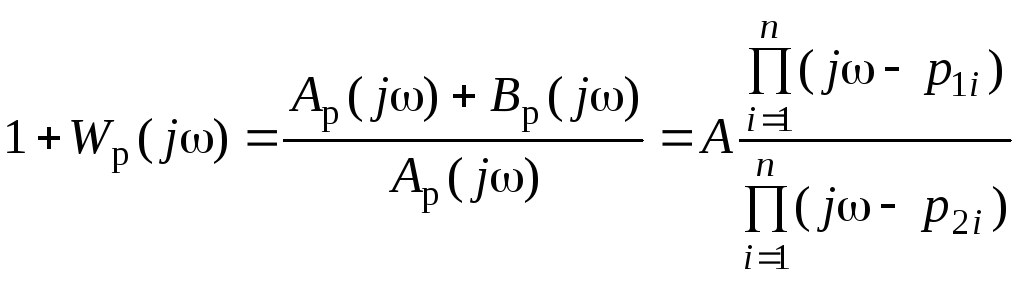где p_1iиp_2i– корни уравненийA_p(j) + B_p(j) = 0 иA_p(j) = 0 соответственно;A– вещественный коэффициент.

В соответствии с первой теоремой Ляпунова, замкнутая система устойчива, если все корниp_1 i лежат в левой полуплоскости. Если разомкнутая система устойчива, то корни уравненияA_p(j) = 0,p_2iтоже лежат в левой полуплоскости. Поскольку при делении комплексных чисел их аргументы вычитаются,arg[1 + W_p(j)] = 0.

Следовательно, что­бы замкнутая система была устойчива, необходимо и достаточно, чтобы годограф вектора {1 + + W_p(j)} не охватывал начало координат прииз­менении  от – до +. При = 0 и присоответственно 1 + W_p(j) = const и  1 + W_p(j)1. Годограф вектора {1 + W_p(j)} представлен нарис.6.7, а.

Если сместить ось ординат вправо на+1,то начало координат в новой системе совпадет с началом вектораW_p(j),а старое началокоординат в новой системе совпадет с точкой(–1;j0) (рис.6.7,б).

Таким образом, критерий Найквиста можно сформулировать следующим образом: чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала точку с координатами (–1; j0).

Заметим, что обратное утверждение является только необходимым, но недостаточным условием неустойчивости системы.

➢   Пример 13. 1. Пусть разомкнутая система является апериодическим звеном второго порядка. Тогда

.

Если T₁ = 0, то АФЧХ имеет вид, показанный нарис.6.8, а,еслиT₁0, то АФЧХ имеет вид, показанный на рис.6.8,б.

Поскольку АФЧХ разомкнутой системы при любых T_i> 0 (i = 1, 2) не пересекает отрицательную полуось абсцисс, система всегда устойчива.

2. Пусть

.

Тогда АФЧХ имеет вид, показанный на рис.6.8, в, и при определенных параметрах, например при увеличенииk, может охватить точку(–1;j0). При этом система потеряет устойчивость.

3. Если последовательно с инерционными звеньями включитьинтегрирующее звено с частотной характеристикой, то умножение вектора АФЧХ, представленного, например, частотной функцией предыдущего примера, на векторс аргументом, равным, означает поворот всех векторовW_p(j) на угол–/2 с одновременным делением на(рис.6.8,г).

Таким образом, АФЧХ приближается к точке (–1; j0) и, следовательно, включение интегрирующего звена в разомкнутую цепь системы уменьшает запас ее устойчивости и увеличивает склонность системы к колебаниям.

4. В случае последовательного включения с инерционными звеньями звена с запаздыванием с АФЧХ W_ (j) = e^–jполучим

W_p(j) = W_p2(j)e^–j = ,

АФЧХ которой представлена на рис.6.8, д.

Как видно из рисунка, введение звена с запаздыванием так же, как и в предыдущем случае, снижает запас устойчивости системы.