§14. Классификация линий второго порядка на проективной плоскости

Пусть на проективной плоскости относительно репера линя второго порядказадается уравнением:.

Левая часть уравнения представляет собой квадратичную форму , определенную на трехмерном векторном пространстве, ненулевые векторы которого порождают точки проективной плоскости. Известно, что заменой базиса, квадратичную форму всегда можно привести к нормальному виду

,

где равныили 0.

При этом ранг и индекс квадратичной формы не зависят от способа приведения её к каноническому виду.

Новый базис векторного пространства порождает новый проективный репер на плоскости, относительно которого линия будет задаваться уравнением

. (_*)

В (*) возможны случаи.

1. Все коэффициенты отличны от нуля ().

а) одного знака.

Уравнение можно привести к виду:.

не содержит ни одной вещественной точки.

–нулевая кривая.

б) разных знаков.

Уравнение можно привести к виду:.

–овальная кривая.

2. Один из коэффициентов равен нулю ().

а) ненулевые коэффициенты одного знака.

Уравнение можно привести к виду:.

–пара мнимых прямых.

б) ненулевые коэффициенты разных знаков.

Уравнение можно привести к виду:.

–пара различных вещественных прямых.

3. Два коэффициента равны нулю ().

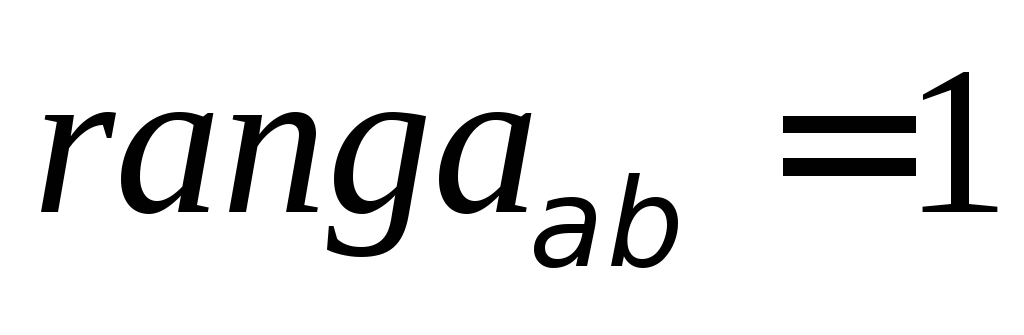Уравнение имеет вид:.

–пара совпавших прямых.

Таким образом, имеем пять типов линий второго порядка на проективной плоскости:

− нулевая и овальная кривые – невырожденные кривые, так как ;

− пара мнимых прямых, пара различных вещественных прямых, пара совпавших прямых – вырожденные кривые, так как .

§15. Овальные линии второго порядка

Т е о р е м а Штейнера. Пусть –проективное, но не перспективное отображение пучка на пучок ,.Множество всех точек пересечения соответствующих прямых является овальной линией второго порядка, проходящей через точки и .

С л е д с т в и е. Прямые иявляются касательными кв точкахи.

Справедлива также

Т е о р е м а, обратная теореме Штейнера. Если и− две точки овальной кривой, то соответствиемежду пучками прямыхП и П, при котором соответствующие прямые пересекаются в точках на линии , касательной в точкесоответствует прямая, а прямойсоответствует касательная в точке, является проективным, но не перспективным отображением пучка на пучок.

Теорема Штейнера позволяет дать геометрическое определение овальной линии второго порядка при помощи проективного, но не перспективного отображения одного пучка прямых на другой.

Обратная теорема устанавливает, что центры этих пучков можно выбирать на овальной кривой произвольно.

С л е д с т в и е 1. Если на плоскости даны пять точек , ни какие три из которых не лежат на одной прямой, то существует единственная овальная кривая второго порядка, проходящая через эти точки.

С л е д с т в и е 2. Если на плоскости даны четыре точки общего положения и прямая, проходящая через точку, то существует единственная овальная кривая второго порядка, проходящая через точки, для которой− касательная в точке.

С л е д с т в и е 3. Если на плоскости даны три точки , не лежащие на одной прямой, и две прямыеи, проходящие соответственно через точкии, и не проходящие через две другие точки, то существует единственная овальная кривая, проходящая через эти три точки, для которой прямаяявляется касательной в точке, а прямая− касательной в точке.

Из доказательства следствия 1 получаем способ построения с помощью одной линейки скольких угодно точек окружности, заданной пятью различными токами.

У п р а ж н е н и е. Пользуясь одной линейкой построить еще одну точку окружности, заданной пятью точками.