
- •§2. -Мерное аффинное пространство
- •§3. Аффинная система координат
- •§4. -Мерные плоскости
- •§5. Уравнения -мерных плоскостей
- •§6. Определение некоторых фигур аффинного пространства
- •Лекция 2.-мерное евклидово (точечное) пространство §7. Евклидово векторное пространство
- •§8. Евклидово -мерное точечное пространство
- •Раздел VI. Проективная геометрия Лекция 1.Проективное n-мерное пространство. Модели проективной прямой и плоскости
- •§1. Центральное проектирование. Предмет проективной геометрии
- •§2. Аксиоматическое определение проективного пространства. Модели проективной прямой и проективной плоскости
- •Лекция 2. Проективные реперы на прямой и плоскости. Уравнение прямой на проективной плоскости §3. Проективные координаты
- •§4. Однородные аффинные координаты
- •§5. Уравнение прямой на проективной плоскости
- •Лекция 3. Принцип двойственности. Теорема Дезарга §6. Принцип двойственности. Теорема Дезарга
- •Лекция 4. Сложные отношения точек и прямых. Гармонические четверки точек и прямых в полном четырехвершиннике §7. Сложное отношение четырех точек прямой
- •§8. Сложное отношение четырех прямых пучка
- •§9. Гармонические четверки
- •Лекция 5. Проективные отображения. Проективные преобразования. Предмет проективной геометрии §10. Проективные преобразования плоскости
- •§11. Проективные отображения прямых и пучков
- •Лекция 6. Квадрики на проективной плоскости. Полюсы и поляры §12. Линии второго порядка на проективной плоскости
- •§13. Полюсы и поляры. Поляритет
- •§14. Классификация линий второго порядка на проективной плоскости
- •§15. Овальные линии второго порядка
- •Лекция 7. Аффинная и евклидова геометрии с проективной точки зрения §16. Проективная модель аффинной плоскости
- •§17. Проективная модель евклидовой плоскости
- •Раздел VII. Топология Лекция 1. Топологическое пространство. Индуцированная топология. Топологические подпространства §1. Метрические пространства
- •§2. Определение и примеры топологических пространств
- •§3. Индуцированная топология. Топологическое подпространство
- •§4. Замкнутые множества
- •§5. Окрестности. Типы точек. Замыкание
- •Лекция 2. Непрерывные отображения и гомеоморфизмы. Предмет топологии. Связность и компактность как основные инварианты топологического пространства §6. Непрерывность и гомеоморфизм
- •§7. Примеры топологических инвариантов
- •Лекция 3. Замкнутые поверхности в трехмерном пространстве и их классификация §8. Понятие поверхности. Замкнутые поверхности
- •§9. Ориентируемость поверхности. Эйлерова характеристика
- •§10. Топологические свойства проективной плоскости
- •Литература
§5. Уравнения -мерных плоскостей
Пусть
в
![]() -мерном
аффинном пространстве
-мерном
аффинном пространстве![]() задана аффинная система координат
задана аффинная система координат![]() .
.
![]() -плоскость
задана точкой
-плоскость
задана точкой
![]() и направляющим подпространством
и направляющим подпространством![]() с базисом
с базисом![]() .
.
Точка
![]() принадлежит плоскости
принадлежит плоскости![]() тогда и только тогда, когда
тогда и только тогда, когда![]() ,
то есть тогда и только тогда, когда
,
то есть тогда и только тогда, когда![]() или
или![]() .
Получилипараметрические
уравнения
.
Получилипараметрические
уравнения
![]() -плоскости
в
-плоскости
в
![]() -мерном
аффинном пространстве (вспомните
параметрические уравнения прямой и
плоскости в геометрическом пространстве).
-мерном
аффинном пространстве (вспомните
параметрические уравнения прямой и
плоскости в геометрическом пространстве).
Из курса алгебры известна теорема о задании подпространства векторного пространства с помощью системы линейных однородных уравнений
Т
е о р е м а. Пусть
дана система
![]() независимых линейных однородных
уравнений
независимых линейных однородных
уравнений
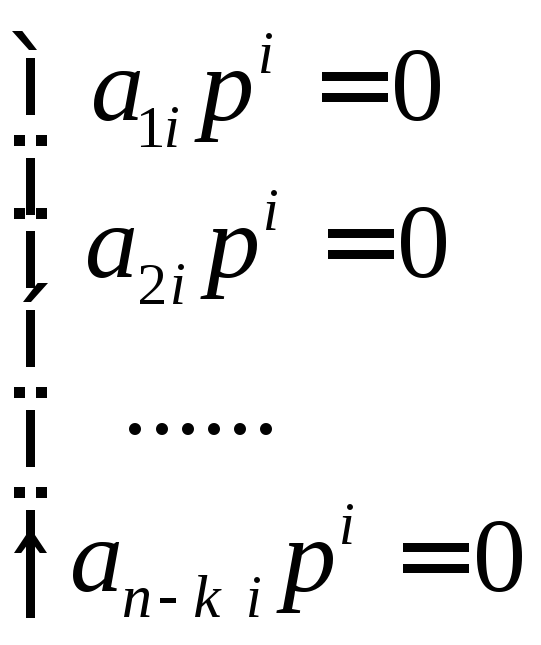
с
![]() неизвестными
неизвестными![]() .
Множество всех векторов
.
Множество всех векторов![]()
![]() -мерного
векторного пространства
-мерного
векторного пространства![]() ,
координаты которых удовлетворяют этой
системе, является
,
координаты которых удовлетворяют этой
системе, является![]() -мерным
векторным подпространством пространства
-мерным
векторным подпространством пространства![]() .
.
Итак,
пусть векторное подпространство
![]() задано системой
задано системой![]() независимых линейных однородных
уравнений. Точка
независимых линейных однородных
уравнений. Точка![]() принадлежит плоскости
принадлежит плоскости![]() тогда и только тогда, когда координаты
вектора
тогда и только тогда, когда координаты
вектора![]() удовлетворяют системе линейных однородных
уравнений, задающих
удовлетворяют системе линейных однородных
уравнений, задающих![]() .
Отсюда имеем
.
Отсюда имеем

систему
![]() независимых линейных уравнений –общие
уравнения
независимых линейных уравнений –общие
уравнения
![]() -плоскости.
-плоскости.
Частные случаи:
Прямая на плоскости (
 )
– одно линейное уравнение.
)
– одно линейное уравнение.Плоскость в трехмерном пространстве (
 )
– одно линейное уравнение.
)
– одно линейное уравнение.Прямая в трёхмерном пространстве (
 )
– система двух независимых линейных
уравнений.
)
– система двух независимых линейных
уравнений.Гиперплоскость в
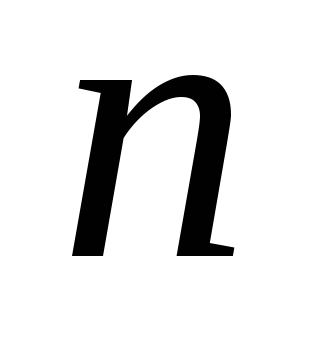 -мерном
пространстве (
-мерном
пространстве ( )
– одно линейное уравнение.
)
– одно линейное уравнение.
Таким
образом, любая
![]() -плоскость
может рассматриваться как пересечение
-плоскость
может рассматриваться как пересечение![]() гиперплоскостей.
гиперплоскостей.
О п р е д е л е н и е. Две плоскости называются пересекающимися, если они имеют хотя бы одну общую точку.
Если две плоскости пересекаются, то их пересечение есть плоскость, направляющее подпространство которой является пересечением направляющих подпространств этих плоскостей.
Если
в
![]() -мерном
аффинном пространстве плоскости
-мерном
аффинном пространстве плоскости![]() и
и![]() таковы, что
таковы, что![]() ,
где
,
где![]() – размерность пересечения направляющих
подпространств, то плоскости
– размерность пересечения направляющих
подпространств, то плоскости![]() и
и![]() пересекаются (рассмотрите случай двух
плоскостей, прямой и плоскости в
геометрическом пространстве).
пересекаются (рассмотрите случай двух
плоскостей, прямой и плоскости в
геометрическом пространстве).
О п р е д е л е н и е. Две плоскости называются параллельными, если они не имеют общих точек и направляющее подпространство одной из них содержится в направляющем подпространстве другой.
О п р е д е л е н и е. Две плоскости называются скрещивающимися, если они не имеют общих точек и не параллельны.
Если сумма размерностей плоскостей больше либо равна размерности пространства, то эти плоскости не могут быть срещивающимися (в геометрическом пространстве две прямые могут быть скрещивающимися, а прямая и плоскость не могут быть скрещивающимися).
§6. Определение некоторых фигур аффинного пространства
О
п р е д е л е н и е. Пусть
![]() три точки одной прямой. Число
три точки одной прямой. Число![]() называетсяпростым
отношением точек
называетсяпростым
отношением точек
![]() ,
если
,
если![]() .
.
Т
е о р е м а 1. Для
любого действительного числа
![]() на прямой
на прямой![]() существует единственная точка
существует единственная точка![]() такая, что
такая, что![]() .
.
О
п р е д е л е н и е. Точка
![]() лежит между точками
лежит между точками![]() и
и![]() (
(![]() ),
если
),
если![]() .
.
Из
теоремы 1 следует, что между точками
![]() и
и![]() лежит бесконечно много точек.
лежит бесконечно много точек.
Т
е о р е м а 2. Если
![]() ,
то
,
то![]() .
.
О
п р е д е л е н и е. Отрезком
с концами
![]() и
и![]() называется фигура, состоящая из точек
называется фигура, состоящая из точек![]() и
и![]() и всех точек, лежащих между ними.
и всех точек, лежащих между ними.
Т
е о р е м а 3. Отрезок
![]() есть множество всех точек
есть множество всех точек![]() таких, что
таких, что![]() .
.
О
п р е д е л е н и е. Лучом
![]() называется фигура состоящая из точек
отрезка
называется фигура состоящая из точек
отрезка![]() и всех точек
и всех точек![]() таких, что
таких, что![]() .
.
О
п р е д е л е н и е. Фигура, состоящая из
всех точек
![]() таких, что
таких, что![]() где
где![]() и
и![]() – линейно независимая система векторов,
называется
– линейно независимая система векторов,
называется
![]() -мерным
параллелепипедом, натянутым на точку
-мерным
параллелепипедом, натянутым на точку![]() и векторы
и векторы![]() (при
(при
![]() имеем отрезок, при
имеем отрезок, при![]() – параллелограмм).
– параллелограмм).
