§2. Определение и примеры топологических пространств

О п р е д е л е н и е. На непустом множестве задана топологическая структура (топология), если задано семейство подмножеств множества, удовлетворяющее условиям

1. ;

2. Объединение любого числа элементов из также принадлежит.

3. Пересечение конечного числа элементов из также принадлежит.

Непустое множество с заданной на нем топологией называется топологическим пространством.

Элементы семейства называютсяоткрытыми множествами.

Примеры топологических пространств

1. Метрическое пространство.

2. Евклидова плоскость с естественной топологией: открытым является любое множество, которое вместе с каждой своей точкой содержит открытый круг с центром в этой точке.

3. , – семейство всех подмножеств множества. Заданная топология называетсядискретной.

4. , . Задаваемая топология называетсяантидискретной.

Из приведенных примеров следует, что на любом непустом множестве можно задать топологию и на одном и том же множестве можно определять различные топологии.

§3. Индуцированная топология. Топологическое подпространство

Пусть – топологическок пространство,– подмножество множества.

Семейство определяет топологию на:

1. и , так как,и.

2. , так как .

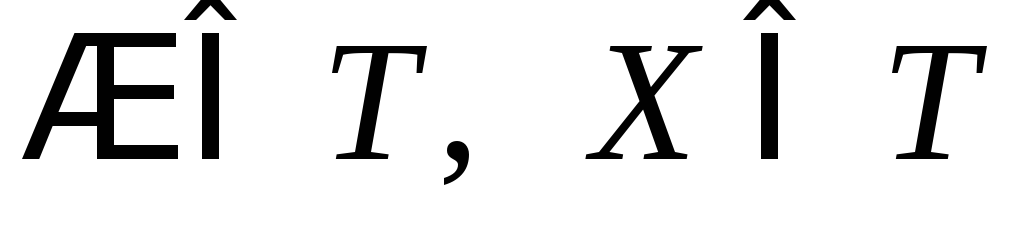3. , так как .

Топология, определяемая на множестве семейством, называетсяиндуцированной топологией; топологическое пространство называетсятопологическим подпространством пространства .

У п р а ж н е н и е. Проверьте, что на евклидовой плоскости семейство множеств, гдеопределяет топологию. Опишите открытые множества в индуцированной топологии на множестве.

§4. Замкнутые множества

Пусть – топологическое пространство. Подмножествомножестваназываетсязамкнутым множеством, если его дополнение доявляется открытым множеством.

У п р а ж н е н и е. Определить все замкнутые множества относительно топологии, определяемой на евклидовой плоскости семейством множеств, где.

Т е о р е м а. ( о свойствах замкнутых множеств). Замкнутые множества топологического пространства обладают следующими свойствами:

. Множества имножество являются замкнутыми множествами.

. Объединение конечного числа замкнутых множеств является замкнутым множеством.

. Пересечение любого числа замкнутых множеств является замкнутым множеством.

Из теоремы следует:

1. Множества являются одновременно и открытыми и замкнутыми.

2. Существуют множества, которые не являются ни открытыми, ни замкнутыми.

3. Часто оказывается удобным задавать топологию на множестве путем выделения семейства замкнутых множеств, удовлетворяющих свойствам.

§5. Окрестности. Типы точек. Замыкание

Пусть – топологическое пространство.

Окрестностью точки называется любое открытое множество, содержащее эту точку.

Точка называетсяточкой прикосновения множества , если любая окрестность точкиимеет хотя бы одну общую точку с.

Замыканием множества называется множество всех его точек прикосновения.

Т е о р е м а. (о свойствах замыканий). Замыкание множества обладает следующими свойствами:

. .

. .

. .

. .

Доказательство свойств . Не вызывает затруднений. Остановимся на доказательстве свойства.

. Сначала покажем, что замыкание множества– это замкнутое множество. Для этого достаточно показать, что множествоявляется открытым. Для любой точкиследует, что эта точка не принадлежит, то есть существует окрестностьточки, не имеющая общих точек с. Тогда эта окрестность не будет иметь общих точек с множеством(предположите противное). Следовательно,и значитможно представить как объединение таких окресностей для всех точек этого множества. Множествоявляется открытым множеством., а значитзамкнутым множеством.

. Далее покажем, что если множество замкнутое, то оно совпадает со своим замыканием. Действительно, если множествозамкнутое, то множествоявляется открытым и является окрестностью каждой своей точки. Так как, то точки множестване являются точками прикосновения множества, то есть все точки прикосновения множествасодержатся в:. Учитывая свойство, получаем.

Из пунктов следует справедливость свойства.

Из свойств следуетещё один способ топологизации множества. Каждому подмножеству множествапоставим в соответствие некоторое подмножество, которое назовем замыканием, с соблюдением свойств. Тогда во множествес такой структурой назовем замкнутыми те подмножества, которые совпадают со своим замыканием. Эти подмножества будут удовлетворять свойствам, следовательно, имеем топологию на( такой способ определения топологии был предложен Куратовским, 1922 г.).

Точка называетсяграничной точкой множества , если любая окрестность этой точки содержит как точки принадлежащие, так и точки не принадлежащие.

Множество всех граничных точек множества называется егограницей .

Очевидно, что граничная точка является точкой прикосновения и множества и множества, следовательно, то есть множествовсеч граничных точек является замкнутым множеством.

Имеем , то есть само топологическое пространство не имеет границы.

Точка называетсявнутренней точкой множества , если существует окрестность этой точки, содержащаяся в . Множествовсех внутренних точек множестваназывается еговнутренностью.

Т е о р е м а. Замыкание множества является объединением его внутренних и граничных точек: .

С л е д с т в и я:

1. , .

2. Множество замкнутое тогда и только тогда, когда оно содержит свою границу.

Можно доказать следующие свойства внутренностей

. .

. .

. .

. .

Поставив каждому подмножеству множествав соответствие некоторое подмножество, с соблюдением свойств, то есть определив операцию взятия внутренности, можно на множествезадать топологию: открытым назовем множество, которое совпадает со своей внутренностью ( такой способ определения топологии был предложен П.С Александровым, 1925 г.).