
- •§2. Уравнение плоскости
- •§3. Условие параллельности плоскости и вектора
- •§4. Взаимное расположение двух плоскостей
- •§5. Геометрический смысл знака четырехчлена плоскости
- •§6. Расстояние от точки до плоскости
- •Лекция 2. Прямая в пространстве §7. Уравнение прямой в пространстве
- •§8. Взаимное расположение прямых. Расстояние между прямыми в пространстве
- •Лекция 3 - 4. Поверхности второго порядка в пространстве §9. Поверхности второго порядка. Метод сечений
- •§10. Цилиндрические поверхности
- •§11. Конические поверхности второго порядка. Конические сечения
- •§12. Поверхности вращения
- •§13. Сжатие пространства к плоскости
- •§14. Эллипсоид
- •§15. Гиперболоиды
- •§16. Параболоиды
- •§17. Прямолинейные образующие поверхностей второго порядка
- •Раздел IV. Геометрические преобразования плоскости и пространства Лекция 1. Отображения, виды отображений
- •§1. Отображение и преобразование множеств
- •§2. Группа преобразований плоскости
- •Лекция 2. Движения плоскости, их геометрические свойства §3. Движения плоскости, их свойства
- •§4. Формулы движений
- •§5. Примеры движений
- •Лекция 3. Классификация движений плоскости §6. Теорема Шаля
- •Лекция 4. Подобия плоскости, их геометрические свойства. Классификация подобий §7. Гомотетия как пример преобразования подобия
- •§8. Свойства подобий
- •Лекция 5. Аффинные преобразования плоскости, их геометрические свойства §9. Аффинные преобразования, их свойства
- •§10. Перспективно-аффинные преобразования
- •§11. Группа аффинных преобразований, её подгруппы. Эрлангенская программа ф. Клейна
- •Лекция 6. Движения пространства, их классификация §12. Движения пространства
- •Литература
§13. Сжатие пространства к плоскости
О п р е
д е л е н и е. Отображение пространства
в себя, при котором каждой точке
![]() соответствует точка
соответствует точка![]() такая,
что
такая,
что![]() ,
где
,
где![]() ,
,![]() – ортогональная проекция точки
– ортогональная проекция точки![]() на данную плоскость
на данную плоскость![]() ,
называетсясжатием
пространства к плоскости
,
называетсясжатием
пространства к плоскости
![]() с коэффициентом
с коэффициентом![]() .
.
Несложно
найти формулы
сжатия к плоскости
![]() :
:
![]() .
.
§14. Эллипсоид
О п р е д е л е н и е. Поверхность, полученная вращением эллипса вокруг его оси симметрии, называется эллипсоидом вращения.
Пусть
в пространстве задана прямоугольная
система координат
![]() и в плоскости
и в плоскости![]() в репере
в репере![]() эллипс задан каноническим уравнением
эллипс задан каноническим уравнением![]() .
Чтобы получить эллипсоид вращения с
осью
.
Чтобы получить эллипсоид вращения с
осью![]() ,
достаточно рассмотреть линию, заданную
уравнением
,
достаточно рассмотреть линию, заданную
уравнением![]() .
.
Поверхность,
полученная при вращении этой линии
вокруг оси
![]() ,
будет задаваться уравнением
,
будет задаваться уравнением![]() .
.
О п р е д е л е н и е. Поверхность, полученная из эллипсоида вращения путем сжатия к плоскости, проходящей через ось вращения, называется эллипсоидом.
Выполнив
сжатие к плоскости
![]() ,
получимканоническое
уравнение эллипсоида:
,
получимканоническое
уравнение эллипсоида:
![]() .
.
Самостоятельно исследовать методом сечений и построить эллипсоид.
§15. Гиперболоиды
О п р е д е л е н и е. Поверхность, полученная вращением гиперболы вокруг её мнимой оси, называется однополостным гиперболоидом вращения.
Пусть
в пространстве задана прямоугольная
система координат
![]() и в плоскости
и в плоскости![]() в репере
в репере![]() гипербола задана каноническим уравнением
гипербола задана каноническим уравнением![]() .
Чтобы получить однополостный гиперболоид
вращения, достаточно рассмотреть одну
ветвь гиперболы, заданную уравнением
.
Чтобы получить однополостный гиперболоид
вращения, достаточно рассмотреть одну
ветвь гиперболы, заданную уравнением![]() .
.
Поверхность,
полученная при вращении этой линии
вокруг оси
![]() ,
будет задаваться уравнением
,
будет задаваться уравнением![]() –каноническое
уравнение однополостного гиперболоида
вращения.
–каноническое
уравнение однополостного гиперболоида
вращения.
О п р е д е л е н и е. Поверхность, полученная из однополостного гиперболоида вращения путем сжатия к плоскости, проходящей через ось вращения, называется однополостным гиперболоидом.
Выполнив
сжатие к плоскости
![]() ,
получимканоническое
уравнение однополостного гиперболоида:
,
получимканоническое
уравнение однополостного гиперболоида:
![]() .
.
Самостоятельно исследовать методом сечений и построить однополостный гиперболоид.
О п р е д е л е н и е. Поверхность, полученная вращением гиперболы вокруг её действительной оси, называется двуполостным гиперболоидом вращения.
Пусть
в пространстве задана прямоугольная
система координат
![]() и в плоскости
и в плоскости![]() в репере
в репере![]() гипербола задана каноническим уравнением
гипербола задана каноническим уравнением![]() .
Чтобы получить двуполостный гиперболоид
вращения, достаточно рассмотреть точки
гиперболы, расположенные в полуплоскости
.
Чтобы получить двуполостный гиперболоид
вращения, достаточно рассмотреть точки
гиперболы, расположенные в полуплоскости![]() .
Это будут точки, задаваемые уравнением:
.
Это будут точки, задаваемые уравнением:![]() .
.
Поверхность,
полученная при вращении этой линии
вокруг оси
![]() ,
будет задаваться уравнением
,
будет задаваться уравнением![]() – каноническое уравнение двуполостного
гиперболоида вращения.
– каноническое уравнение двуполостного
гиперболоида вращения.
О п р е д е л е н и е. Поверхность, полученная из двуполостного гиперболоида вращения путем сжатия к плоскости, проходящей через ось вращения, называется двуполостным гиперболоидом.
Выполнив
сжатие к плоскости
![]() ,
получимканоническое
уравнение двуполостного гиперболоида:
,
получимканоническое
уравнение двуполостного гиперболоида:
![]() .
.
Самостоятельно исследовать методом сечений и построить двуполостный гиперболоид.
§16. Параболоиды
О п р е д е л е н и е. Поверхность, полученная вращением параболы вокруг её оси, называется параболоидом вращения.
Пусть
в пространстве задана прямоугольная
система координат
![]() и в плоскости
и в плоскости![]() в репере
в репере![]() парабола задана каноническим уравнением
парабола задана каноническим уравнением![]() .
Чтобы получить параболоид вращения,
достаточно рассмотреть одну ветвь
параболы, заданную уравнением
.
Чтобы получить параболоид вращения,
достаточно рассмотреть одну ветвь
параболы, заданную уравнением![]() .
.
Поверхность,
полученная при вращении этой линии
вокруг оси
![]() ,
будет задаваться уравнением
,
будет задаваться уравнением![]() –каноническое
уравнение параболоида вращения.
–каноническое
уравнение параболоида вращения.
О п р е д е л е н и е. Поверхность, полученная из параболоида вращения путем сжатия к плоскости, проходящей через ось вращения, называется эллиптическим параболоидом.
Выполнив
сжатие к плоскости
![]() ,
получимканоническое
уравнение эллиптического параболоида:
,
получимканоническое
уравнение эллиптического параболоида:
![]() .
.
Исследование эллиптического параболоида методом сечений:
Из уравнения следует, что плоскости
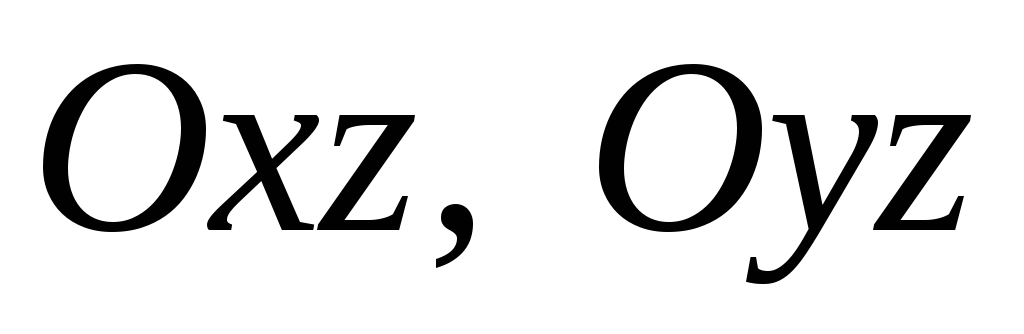 являются плоскостями симметрии, а ось
являются плоскостями симметрии, а ось – осью симметрии.
– осью симметрии.При пересечении эллиптического параболоида с плоскостью
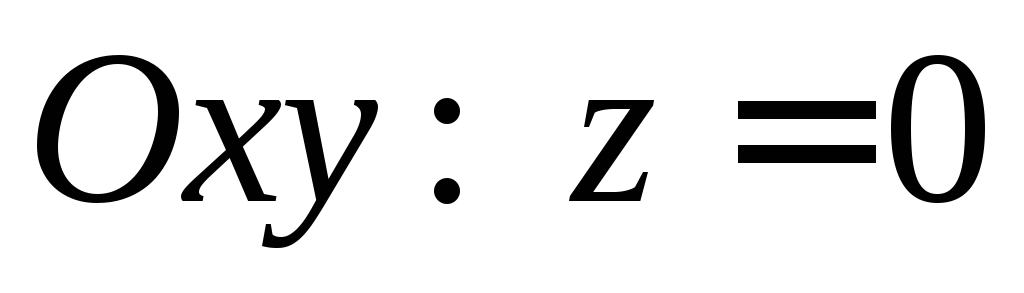 получаем точку
получаем точку – вершина эллиптического параболоида.
– вершина эллиптического параболоида.При пресечении эллиптического параболоида с плоскостью
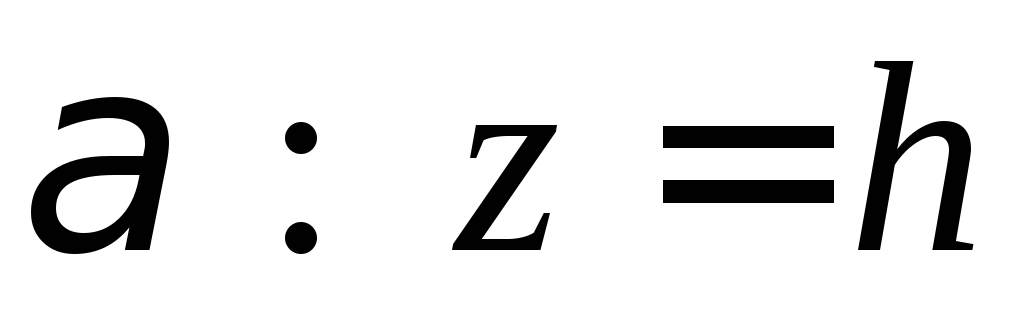 ,
параллельной плоскости
,
параллельной плоскости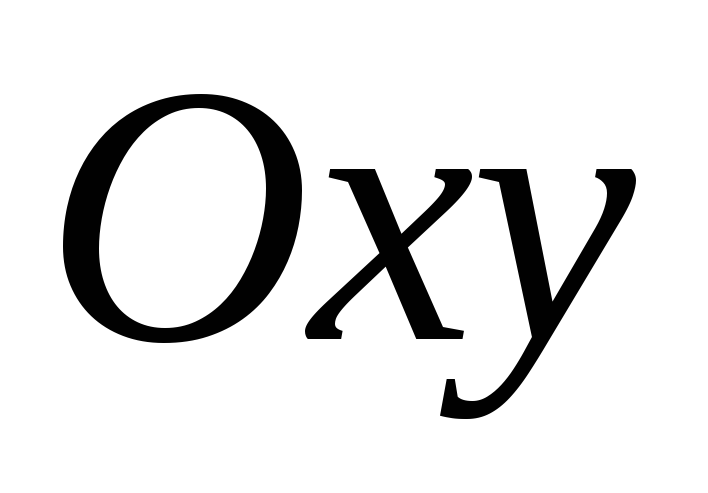 ,
получаем эллипс (
,
получаем эллипс (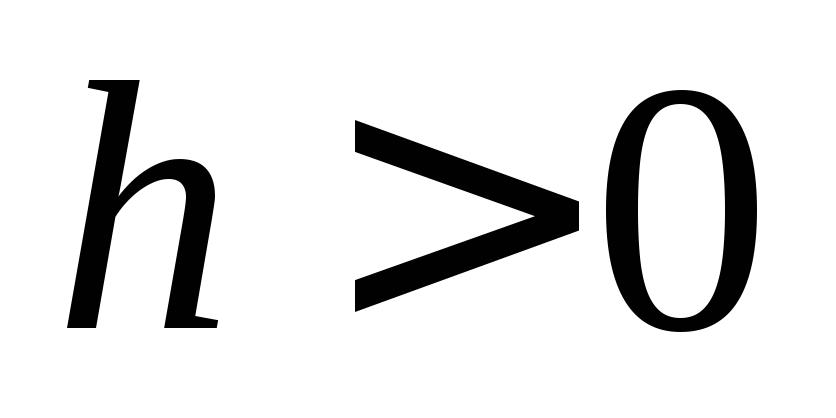 )
или мнимый эллипс (
)
или мнимый эллипс (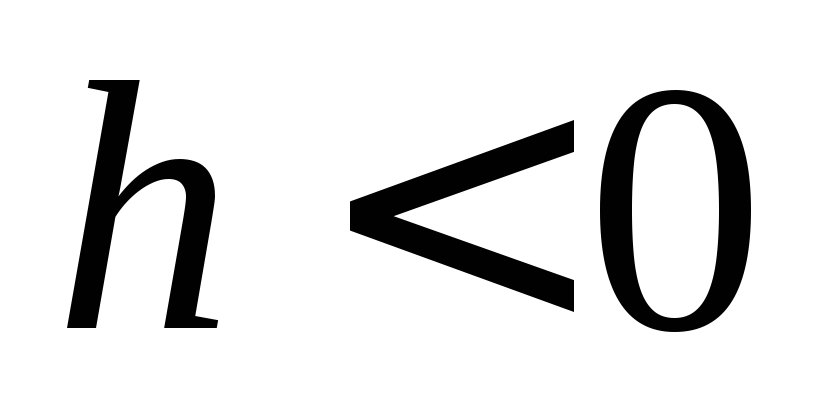 ).
).При пересечении эллиптического параболоида с плоскостью
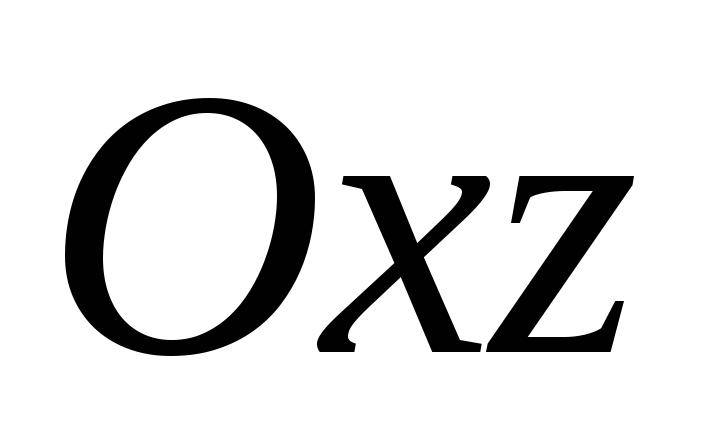 или плоскостями ей параллельными (
или плоскостями ей параллельными (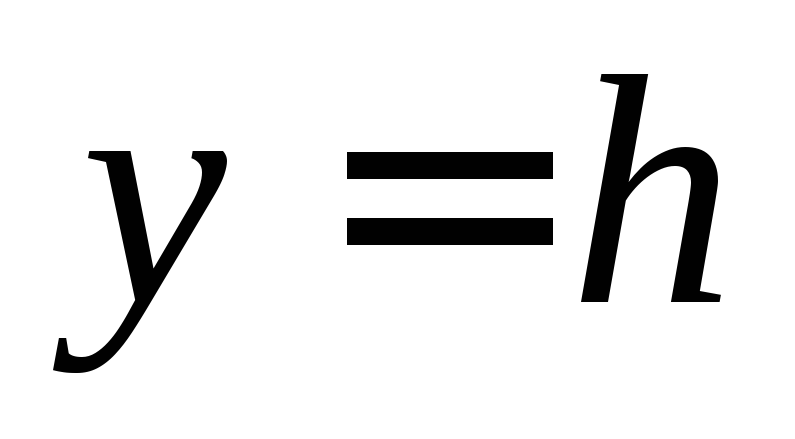 ),
получаем параболы
),
получаем параболы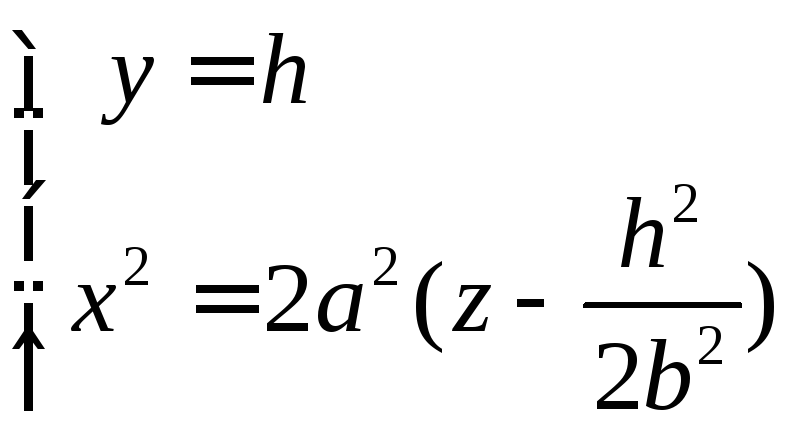 с одним и тем же фокальным параметром
с одним и тем же фокальным параметром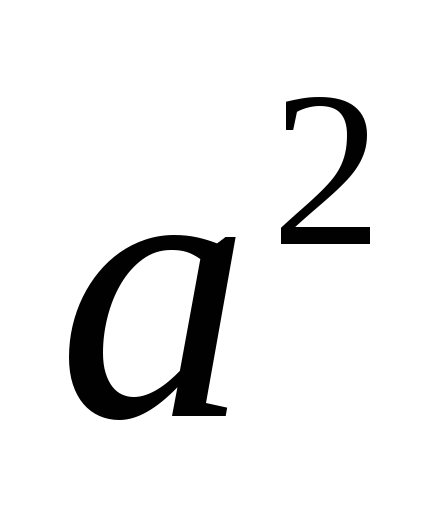 .
То есть это будут одинаковые параболы,
расположенные в параллельных плоскостях.
.
То есть это будут одинаковые параболы,
расположенные в параллельных плоскостях.Аналогично, при пересечении эллиптического параболоида с плоскостью
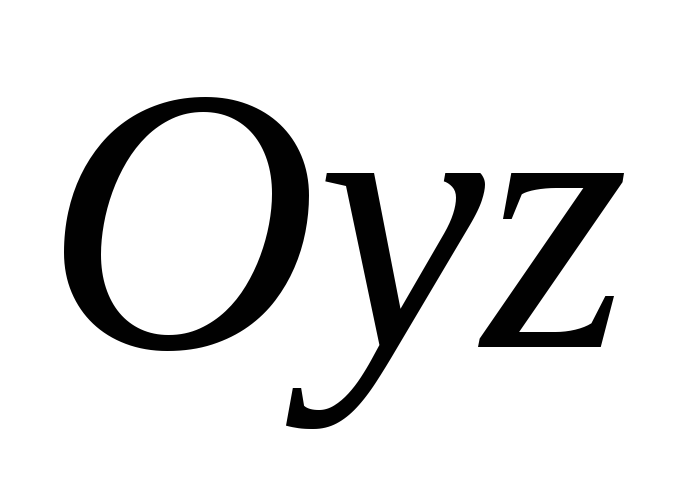 и параллельными ей плоскостями, будем
получать одинаковые параболы с фокальным
параметром
и параллельными ей плоскостями, будем
получать одинаковые параболы с фокальным
параметром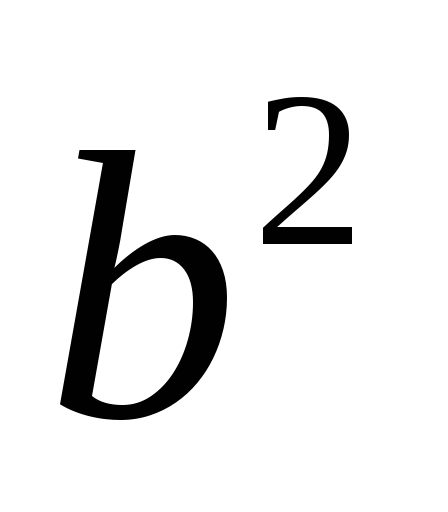 .
.
Из пунктов 4 и 5 исследования эллиптического параболоида методом сечений следует другой способ получения эллиптического параболоида.
Пусть
![]() – две параболы с общей вершиной, общей
осью, расположенные в перпендикулярных
плоскостях, и их ветви направлены в одну
сторону. Тогда, поверхность, полученная
смещением одной параболы параллельно
самой себе так, что её вершина скользит
по другой параболе, будет эллиптическим
параболоидом.
– две параболы с общей вершиной, общей
осью, расположенные в перпендикулярных
плоскостях, и их ветви направлены в одну
сторону. Тогда, поверхность, полученная
смещением одной параболы параллельно
самой себе так, что её вершина скользит
по другой параболе, будет эллиптическим
параболоидом.
Пусть
![]() – неподвижная парабола, а
– неподвижная парабола, а![]() – подвижная парабола. Можно показать,
что координаты любой точки
– подвижная парабола. Можно показать,
что координаты любой точки![]() поверхности Ф, образованной смещением
поверхности Ф, образованной смещением![]() параллельно самой себе так, что её
вершина скользит по параболе
параллельно самой себе так, что её
вершина скользит по параболе![]() ,
и только координаты этих точек будут
удовлетворять уравнению
,
и только координаты этих точек будут
удовлетворять уравнению![]() .
То есть поверхность Ф является
эллиптическим параболоидом.
.
То есть поверхность Ф является
эллиптическим параболоидом.
Если
![]() – две параболы с общей вершиной, общей
осью, расположенные в перпендикулярных
плоскостях, и их ветви направлены в
противоположные стороны, то уравнение
поверхности Ф, полученной смещением
одной параболы параллельно самой себе
так, что её вершина скользит по другой
параболе, будет иметь вид
– две параболы с общей вершиной, общей
осью, расположенные в перпендикулярных
плоскостях, и их ветви направлены в
противоположные стороны, то уравнение
поверхности Ф, полученной смещением
одной параболы параллельно самой себе
так, что её вершина скользит по другой
параболе, будет иметь вид![]() или
или![]() .
Поверхность, задаваемая таким уравнением,
называетсягиперболическим
параболоидом (сечения
плоскостями, параллельными координатным
плоскостям, являются либо гиперболами,
либо параболами).
.
Поверхность, задаваемая таким уравнением,
называетсягиперболическим
параболоидом (сечения
плоскостями, параллельными координатным
плоскостям, являются либо гиперболами,
либо параболами).
