
- •§2. Уравнение плоскости
- •§3. Условие параллельности плоскости и вектора
- •§4. Взаимное расположение двух плоскостей
- •§5. Геометрический смысл знака четырехчлена плоскости
- •§6. Расстояние от точки до плоскости
- •Лекция 2. Прямая в пространстве §7. Уравнение прямой в пространстве
- •§8. Взаимное расположение прямых. Расстояние между прямыми в пространстве
- •Лекция 3 - 4. Поверхности второго порядка в пространстве §9. Поверхности второго порядка. Метод сечений
- •§10. Цилиндрические поверхности
- •§11. Конические поверхности второго порядка. Конические сечения
- •§12. Поверхности вращения
- •§13. Сжатие пространства к плоскости
- •§14. Эллипсоид
- •§15. Гиперболоиды
- •§16. Параболоиды
- •§17. Прямолинейные образующие поверхностей второго порядка
- •Раздел IV. Геометрические преобразования плоскости и пространства Лекция 1. Отображения, виды отображений
- •§1. Отображение и преобразование множеств
- •§2. Группа преобразований плоскости
- •Лекция 2. Движения плоскости, их геометрические свойства §3. Движения плоскости, их свойства
- •§4. Формулы движений
- •§5. Примеры движений
- •Лекция 3. Классификация движений плоскости §6. Теорема Шаля
- •Лекция 4. Подобия плоскости, их геометрические свойства. Классификация подобий §7. Гомотетия как пример преобразования подобия
- •§8. Свойства подобий
- •Лекция 5. Аффинные преобразования плоскости, их геометрические свойства §9. Аффинные преобразования, их свойства
- •§10. Перспективно-аффинные преобразования
- •§11. Группа аффинных преобразований, её подгруппы. Эрлангенская программа ф. Клейна
- •Лекция 6. Движения пространства, их классификация §12. Движения пространства
- •Литература
§17. Прямолинейные образующие поверхностей второго порядка
Прямая
![]() называетсяпрямолинейной
образующей поверхности Ф,
если каждая точка этой прямой принадлежит
поверхности Ф.
называетсяпрямолинейной
образующей поверхности Ф,
если каждая точка этой прямой принадлежит
поверхности Ф.
Образующие цилиндрической и конической поверхностей являются их прямолинейными образующими.
Так как все точки эллипсоида находятся внутри параллелепипеда, то эллипсоид не имеет прямолинейных образующих.
Покажите, что двуполостный гиперболоид и эллиптический параболоид не имеют прямолинейных образующих.
Представив уравнение
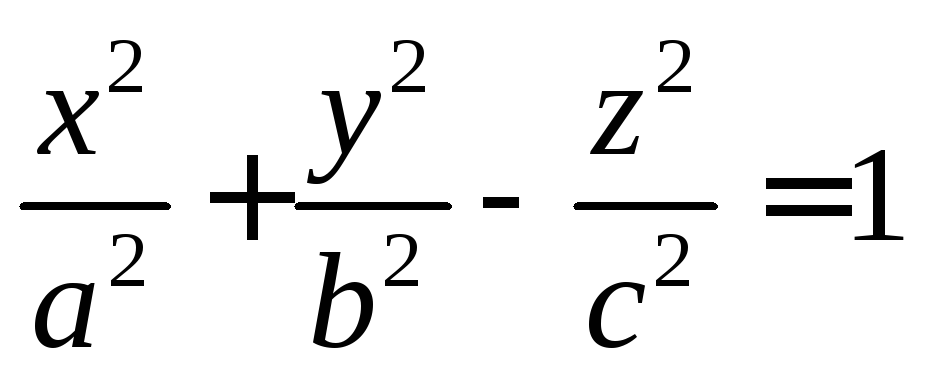 однополостного гиперболоида в виде
однополостного гиперболоида в виде
![]() ,
,
несложно
заметить, что для каждого действительного
числа
![]() каждая из прямых, определяемых уравнениями
каждая из прямых, определяемых уравнениями
 ,
,
целиком лежат на однополостном гиперболоиде, а значит, является прямолинейной образующей.
Таким образом, на однополостном гиперболоиде имеем два семейства прямолинейных образующих, обладающие свойствами:
Через каждую точку поверхности проходит в точности по одной прямолинейной образующей из каждого семейства.
Две прямолинейные образующие одного семейства скрещиваются.
Две прямолинейные образующие разных семейств лежат в одной плоскости.
Аналогично можно показать, что на гиперболическом параболоиде существуют два семейства прямолинейных образующих, обладающие свойствами a-c и свойством
Все прямолинейные образующие одного семейства параллельны одной плоскости.
Раздел IV. Геометрические преобразования плоскости и пространства Лекция 1. Отображения, виды отображений
Раздел преобразования плоскости и пространства является одним из интереснейших и важнейших в курсе геометрии:
он дает аппарат для доказательства многих теорем и решения задач;
это материал для внеурочной работы с учащимися;
теория преобразований позволяет рассматривать с единой точки зрения всё разнообразие геометрических систем.
§1. Отображение и преобразование множеств
Необходимо
вспомнить из вводного курса математики
определения отображения множества
![]() во множество
во множество![]() ,
видов отображений (инъективного,
сюръективного, биективного) и их признаки:
,
видов отображений (инъективного,
сюръективного, биективного) и их признаки:
При инъективном отображении
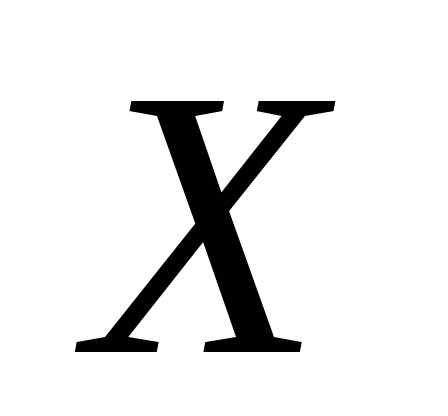 в
в каждый элемент из
каждый элемент из имеет не более одного прообраза.
имеет не более одного прообраза.При сюръективном отображении
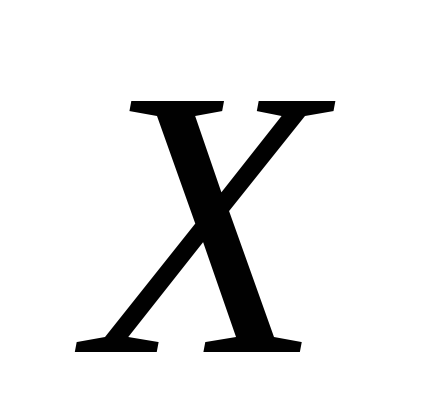 в
в каждый элемент из
каждый элемент из имеет хотя бы один прообраз.
имеет хотя бы один прообраз.При биективном отображении
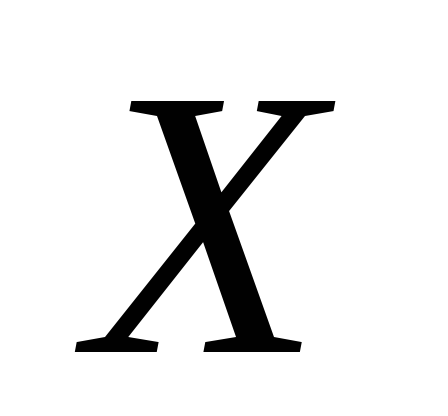 в
в каждый элемент из
каждый элемент из имеет единственный прообраз.
имеет единственный прообраз.
Если
отображение
![]() является биекцией, то существует обратное
ему отображение
является биекцией, то существует обратное
ему отображение![]() ,
при котором
,
при котором![]() ,
если
,
если![]() .
.
Преобразованием
множества
![]() называется биективное отображение
этого множества в себя.
называется биективное отображение
этого множества в себя.
§2. Группа преобразований плоскости
Пусть
![]() – множество всех преобразований
плоскости. На этом множестве можно
определить бинарную операцию (композицию
преобразований
– множество всех преобразований
плоскости. На этом множестве можно
определить бинарную операцию (композицию
преобразований
![]() ):
):![]() – преобразование плоскости, представляющее
собой последовательное выполнение
преобразований
– преобразование плоскости, представляющее
собой последовательное выполнение
преобразований![]() и
и![]() (порядок выполнения преобразований в
записи: справа налево).
(порядок выполнения преобразований в
записи: справа налево).
Т е о р
е м а. Множество
![]() всех преобразований плоскости является
группой относительно композиции
преобразований.
всех преобразований плоскости является
группой относительно композиции
преобразований.
Пусть
![]() некоторая подгруппа группы преобразований
некоторая подгруппа группы преобразований![]() (вспомнить признак подгруппы).Фигура
(вспомнить признак подгруппы).Фигура
![]() называется эквивалентной фигуре
называется эквивалентной фигуре![]() относительно группы
относительно группы
![]() (
(![]() ),
если существует преобразование
),
если существует преобразование![]() ,
что
,
что![]() .
Можно показать, что эквивалентность
фигур относительно группы преобразований
является отношением эквивалентности.
.
Можно показать, что эквивалентность
фигур относительно группы преобразований
является отношением эквивалентности.
Лекция 2. Движения плоскости, их геометрические свойства §3. Движения плоскости, их свойства
Преобразование плоскости, сохраняющее расстояния, называется движением (перемещением) плоскости.
Примеры движений
Тождественное преобразование.
Параллельный перенос.
Параллельным
переносом
![]() на
вектор
на
вектор
![]() называется отображение плоскости в
себя, при котором каждой точке
называется отображение плоскости в
себя, при котором каждой точке![]() плоскости ставится в соответствие точка
плоскости ставится в соответствие точка![]() такая, что
такая, что![]() .
.
Отметим, что параллельный перенос определяется как отображение и, следовательно нужно доказать, что он является преобразованием плоскости (сделайте это самостоятельно).
Имеем
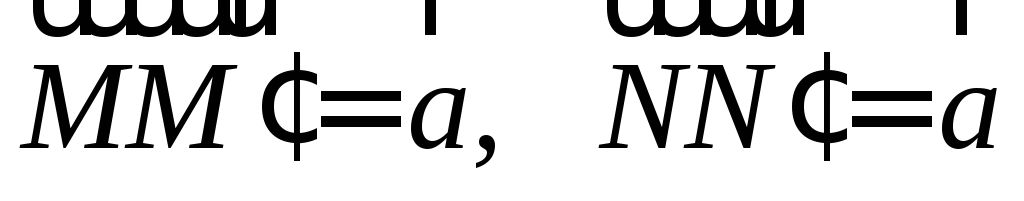 .
Тогда
.
Тогда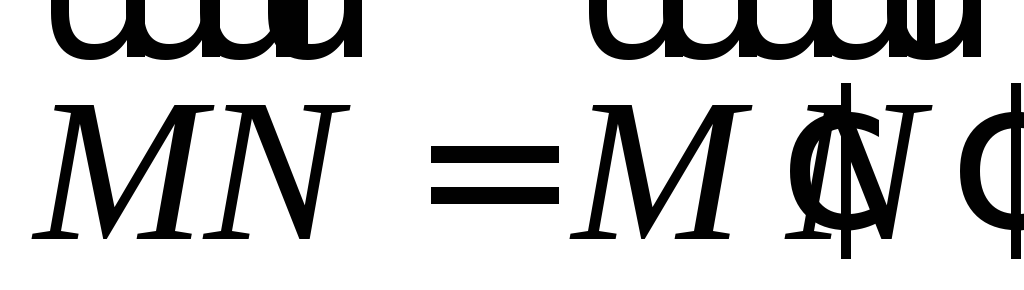 и
и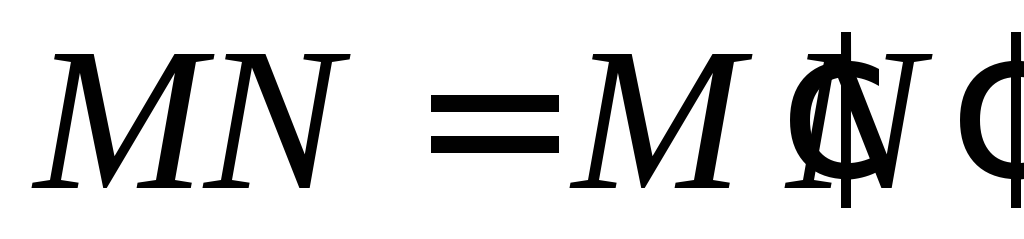 ,
то есть параллельный перенос сохраняет
расстояния, а значит является движением
плоскости.
,
то есть параллельный перенос сохраняет
расстояния, а значит является движением
плоскости.
Центральная симметрия.
Центральной
симметрией
![]() относительно точки
относительно точки
![]() называется отображение плоскости в
себя, при котором каждой точке
называется отображение плоскости в
себя, при котором каждой точке![]() плоскости ставится в соответствие точка
плоскости ставится в соответствие точка![]() такая, что
такая, что![]() .
.
Аналогично нужно показать, что центральная симметрия является преобразованием плоскости.
Из условий
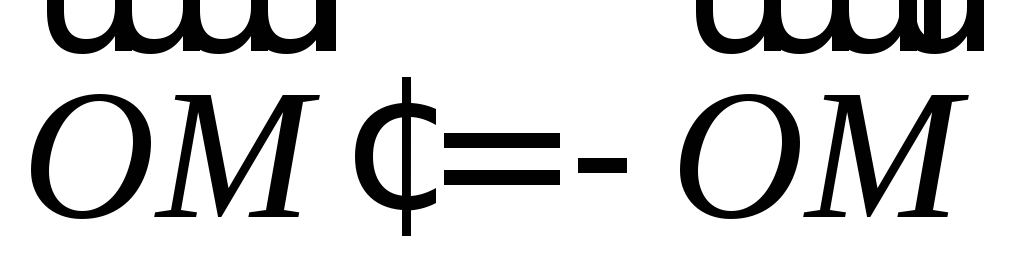 и
и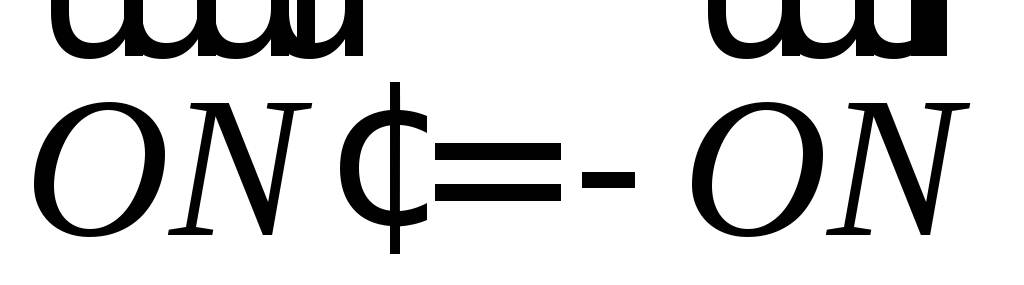 получаем, что
получаем, что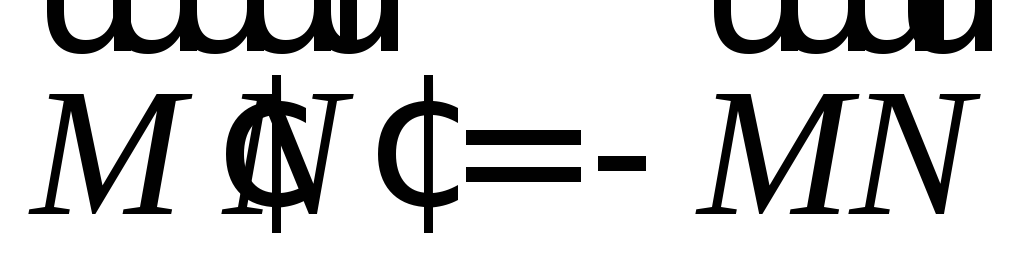 .
Тогда
.
Тогда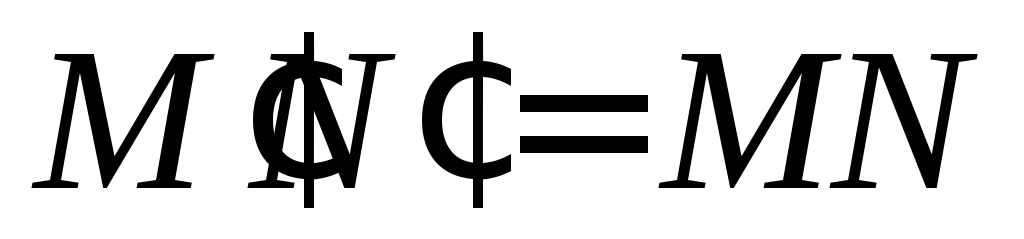 ,
то есть центральная симметрия сохраняет
расстояния, а значит, является движением
плоскости.
,
то есть центральная симметрия сохраняет
расстояния, а значит, является движением
плоскости.
Самостоятельно следует рассмотреть доказательство следующих важных теорем
Т е о р е м а 1. При движении образом репера является репер. Образом оротнормированного репера является ортонормированный репер.
Т
е о р е м а 2. (о
задании движения парой соответствующих
ортонормированных реперов)
Пусть
![]() и
и![]() два ортонормированных репера. Существует
единственное движение плоскости, которое
репер
два ортонормированных репера. Существует
единственное движение плоскости, которое
репер![]() переводит в репер
переводит в репер![]() .
При этом движении каждая точка
.
При этом движении каждая точка![]() с координатами
с координатами![]() в репере
в репере![]() переходит в точку
переходит в точку![]() с теми же координатами в репере
с теми же координатами в репере![]() .
.
Теоремы 1-2 позволяют доказать следующие свойства движений:
Движение переводит прямую в прямую, праллельные прямые в параллельные прямые.
Движение переводит полуплоскость в полуплоскость.
Движение сохраняет простое отношение трех точек прямой, а значит сохраняет отношение «лежать между», а значит переводит отрезок в отрезок, луч в луч, угол в угол.
Движение переводит угол в равный угол, перпендикулярные прямые в перпендикулярные прямые.
Любое движение либо сохраняет ориентацию плоскости (любой репер переводит в одинаково ориентированный с ним репер), либо меняет ориентацию плоскости (любой репер переводит в противоположно ориентированный с ним репер). Отсюда имеем два вида движений: движения I рода (сохраняющие ориентацию плоскости) и движения II рода (меняющие ориентацию плоскости).
