
- •§2. Уравнение плоскости
- •§3. Условие параллельности плоскости и вектора
- •§4. Взаимное расположение двух плоскостей
- •§5. Геометрический смысл знака четырехчлена плоскости
- •§6. Расстояние от точки до плоскости
- •Лекция 2. Прямая в пространстве §7. Уравнение прямой в пространстве
- •§8. Взаимное расположение прямых. Расстояние между прямыми в пространстве
- •Лекция 3 - 4. Поверхности второго порядка в пространстве §9. Поверхности второго порядка. Метод сечений
- •§10. Цилиндрические поверхности
- •§11. Конические поверхности второго порядка. Конические сечения
- •§12. Поверхности вращения
- •§13. Сжатие пространства к плоскости
- •§14. Эллипсоид
- •§15. Гиперболоиды
- •§16. Параболоиды
- •§17. Прямолинейные образующие поверхностей второго порядка
- •Раздел IV. Геометрические преобразования плоскости и пространства Лекция 1. Отображения, виды отображений
- •§1. Отображение и преобразование множеств
- •§2. Группа преобразований плоскости
- •Лекция 2. Движения плоскости, их геометрические свойства §3. Движения плоскости, их свойства
- •§4. Формулы движений
- •§5. Примеры движений
- •Лекция 3. Классификация движений плоскости §6. Теорема Шаля
- •Лекция 4. Подобия плоскости, их геометрические свойства. Классификация подобий §7. Гомотетия как пример преобразования подобия
- •§8. Свойства подобий
- •Лекция 5. Аффинные преобразования плоскости, их геометрические свойства §9. Аффинные преобразования, их свойства
- •§10. Перспективно-аффинные преобразования
- •§11. Группа аффинных преобразований, её подгруппы. Эрлангенская программа ф. Клейна
- •Лекция 6. Движения пространства, их классификация §12. Движения пространства
- •Литература
Лекция 3. Классификация движений плоскости §6. Теорема Шаля
З
а д а ч а 1. Доказать, что композиция двух
осевых симметрий с пересекающимися
осями есть поворот вокруг точки пресечения
на угол в два раза больший, чем угол
между осями, и направленный от первой
оси ко второй:
![]() .
.
С л е д с т в и е. Любой поворот можно представить в виде композиции осевых симметрий с пересекающимися осями, и таких разложений бесконечно много.
Ответьте на вопрос: «Как выбирать оси таких осевых симметрий?»
З
а д а ч а 2. Доказать, что композиция двух
осевых симметрий с параллельными осями
есть параллельный перенос на вектор,
перпендикулярный осям, направленный
от первой оси ко второй, длина которого
равна удвоенному расстоянию между
осями:
![]() .
.
С л е д с т в и е. Любой параллельный перенос можно представить в виде композиции двух осевых симметрий с параллельными осями, и таких разложений бесконечно много.
Ответьте на вопрос: «Как выбирать оси таких осевых симметрий?»
Т е о р е м а 1. (о разложении движения в композицию осевых симметрий). Всякое движение можно представить в виде композиции не более трех осевых симметрий.
Д
о к а з а т е л ь с т в о. Идея доказательства
состоит в следующем. Пусть
![]() движение плоскости. Выберем произвольный
ортонормированный репер
движение плоскости. Выберем произвольный
ортонормированный репер![]() .
Тогда
.
Тогда![]() так же ортонормированный репер. Почему?
так же ортонормированный репер. Почему?
Пара
ортонормированных реперов
![]() и
и![]() однозначно определяет движение. Таким
образом, если покажем существование
композиции не более трех осевых симметрий,
переводящей репер
однозначно определяет движение. Таким
образом, если покажем существование
композиции не более трех осевых симметрий,
переводящей репер![]() в репер
в репер![]() ,
то эта композиция будет совпадать с
движением
,
то эта композиция будет совпадать с
движением![]() .
.
В
случае, когда начала реперов совпадают,
репер
![]() перейдет в репер
перейдет в репер![]() в результате композиции симметрии
относительно серединного перпендикуляра
к отрезку
в результате композиции симметрии
относительно серединного перпендикуляра
к отрезку![]() и симметрии относительно прямой
и симметрии относительно прямой![]() .
.
Если
точки
![]() и
и![]() не совпадают, то при симметрии относительно
серединного перпендикуляра к отрезку
не совпадают, то при симметрии относительно
серединного перпендикуляра к отрезку![]() репер
репер![]() перейдет в репер
перейдет в репер![]() ,
имеющий с репером
,
имеющий с репером![]() общее начало. По предыдущему случаю
репер
общее начало. По предыдущему случаю
репер![]() переходит в репер
переходит в репер![]() в результате двух осевых симметрий.
Тогда репер
в результате двух осевых симметрий.
Тогда репер![]() перейдет в репер
перейдет в репер![]() в результате трех осевых симметрий.
в результате трех осевых симметрий.
Т е о р е м а Ш а л я. Любое движение плоскости является либо параллельным переносом, либо поворотом, либо осевой симметрией, либо скользящей симметрией.
Д
о к а з а т е л ь с т в о. По предыдущей
теореме движение
![]() можно представить в виде композиции не
более трех осевых симметрий. Возможны
случаи:
можно представить в виде композиции не
более трех осевых симметрий. Возможны
случаи:
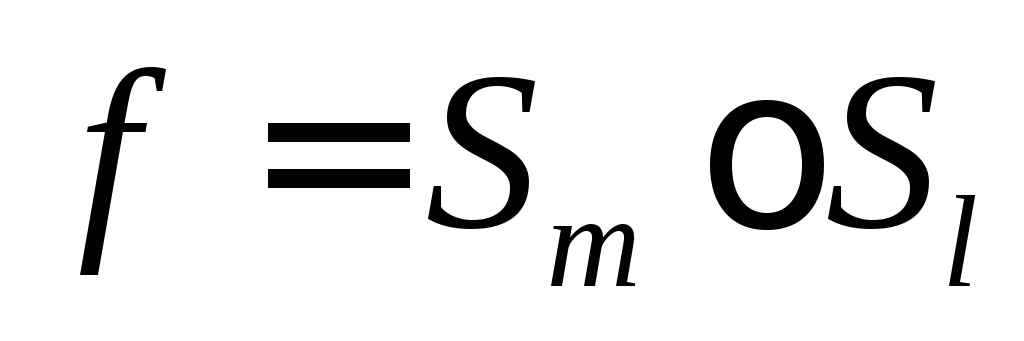
 ,
тогда
,
тогда
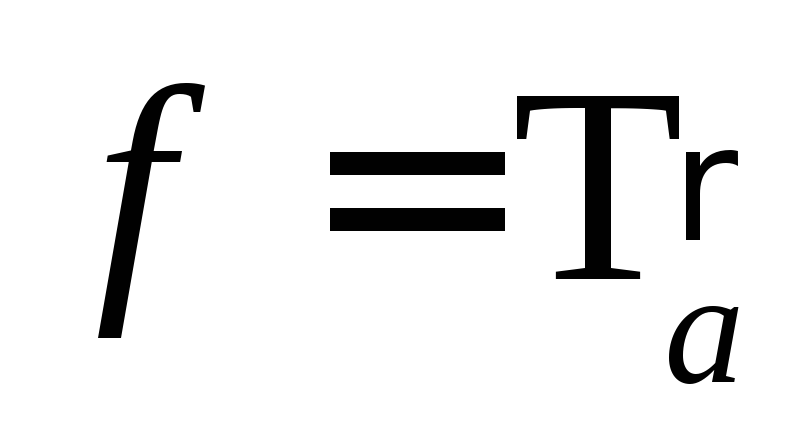 ;
; ,
тогда
,
тогда 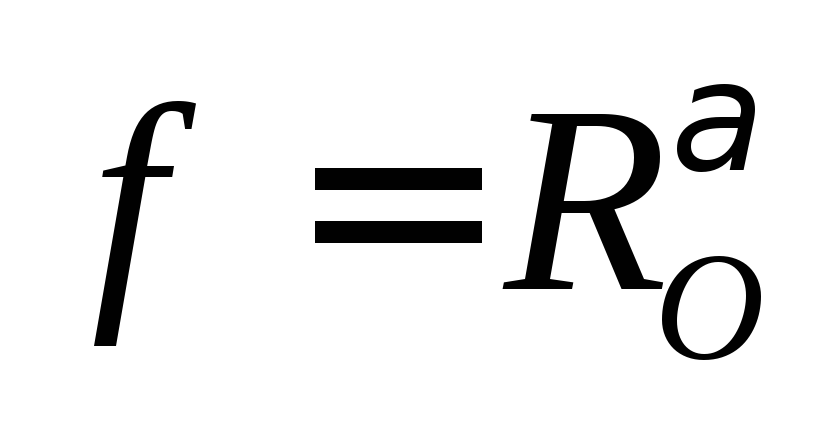 .
.

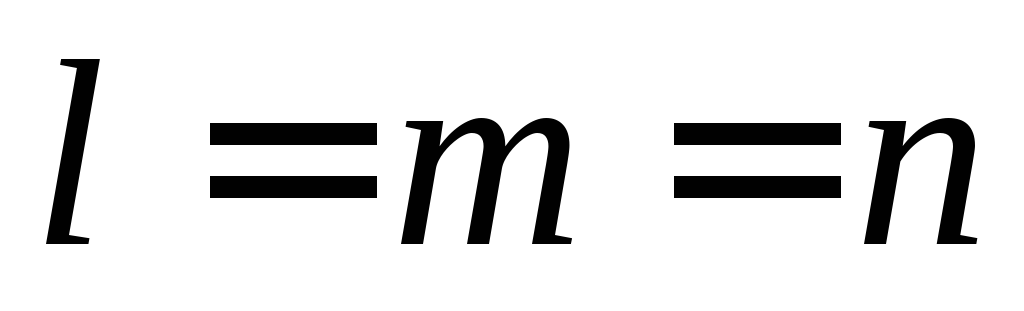 ,
тогда
,
тогда 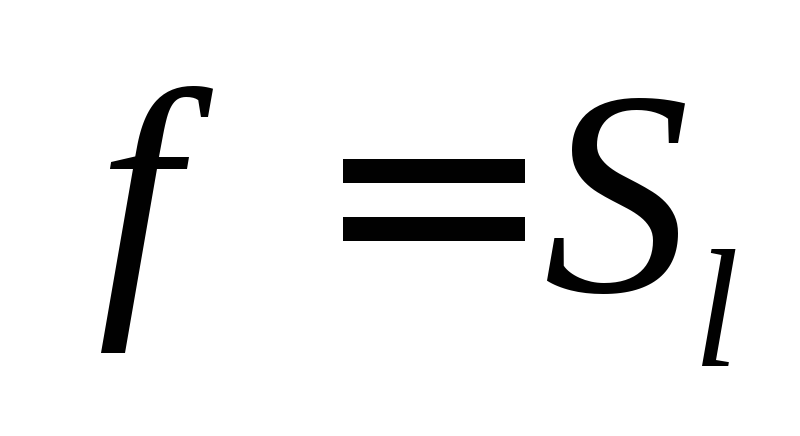 ;
;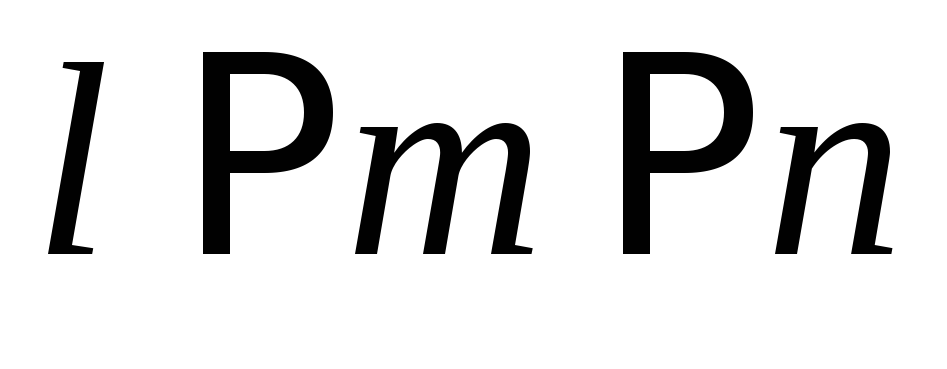 ,
тогда
,
тогда 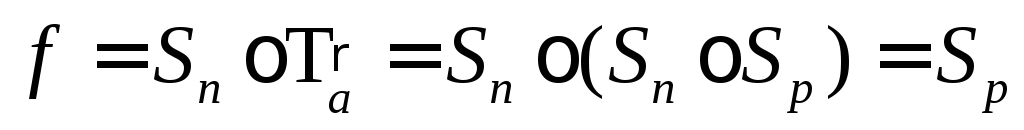 ;
;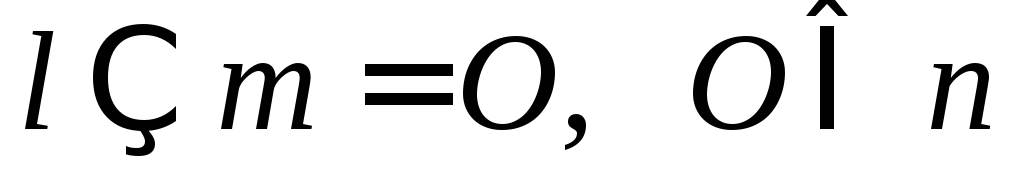 ,
тогда
,
тогда
![]() ;
;
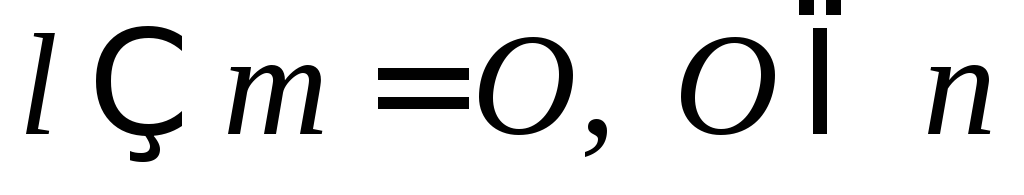 ,
тогда
,
тогда
![]() ,
где
,
где
![]() .
.
Тогда
![]() ,
где
,
где![]() .
Таким образом,
.
Таким образом,![]() ,
где
,
где![]() и, следовательно
и, следовательно![]() .
.
Теорема доказана.
Множество
![]() всех движений плоскости является группой
относительно композиции преобразований.
Подгруппами этой группы являются
множество Т всех параллельных переносов,
множество
всех движений плоскости является группой
относительно композиции преобразований.
Подгруппами этой группы являются
множество Т всех параллельных переносов,
множество![]() всех движений первого рода.
всех движений первого рода.
Фигуры
![]() и
и![]() называются конгруэнтными,
если они эквивалентны относительно
группы
называются конгруэнтными,
если они эквивалентны относительно
группы
![]() всех движений плоскости. Примерами
конгруэнтных фигур являются два
треугольника, соответственные стороны
которых равны, два эллипса (две гиперболы),
соответственные полуоси которых равны,
две параболы, фокальные параметры
которых равны.
всех движений плоскости. Примерами
конгруэнтных фигур являются два
треугольника, соответственные стороны
которых равны, два эллипса (две гиперболы),
соответственные полуоси которых равны,
две параболы, фокальные параметры
которых равны.
Лекция 4. Подобия плоскости, их геометрические свойства. Классификация подобий §7. Гомотетия как пример преобразования подобия
О
п р е д е л е н и е. Подобием
с коэффициентом
![]() называется преобразование плоскости,
при котором все расстояния умножаются
на
называется преобразование плоскости,
при котором все расстояния умножаются
на![]() .
.
Примеры подобий
Любое движение является подобием с коэффициентом
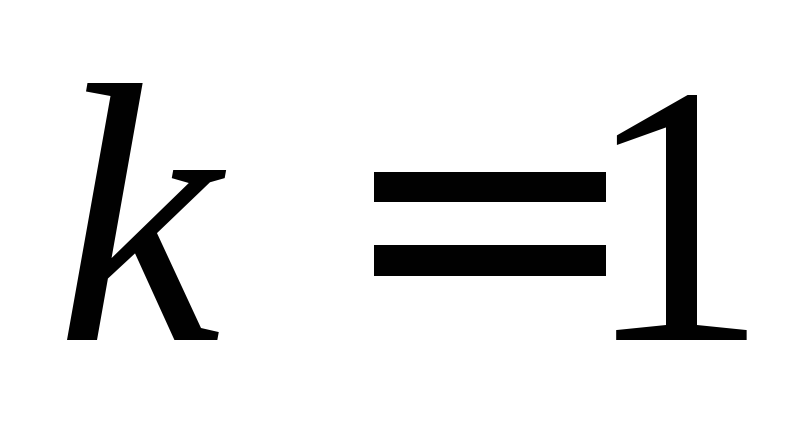 .
.Гомотетией
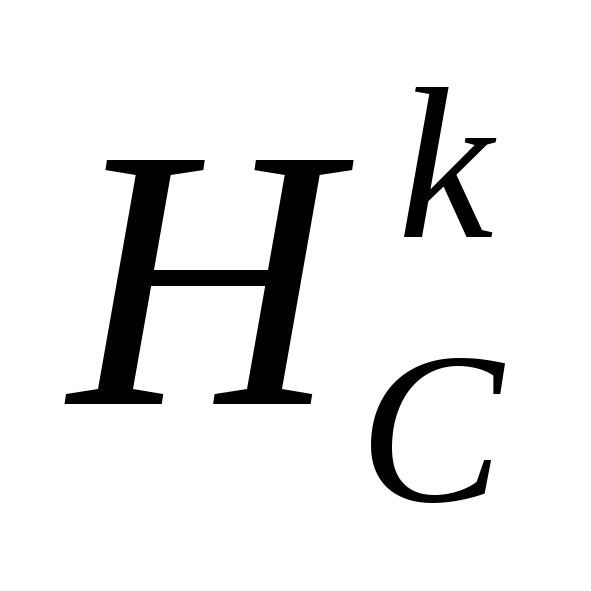 с центорм
с центорм и коэффициентом
и коэффициентом
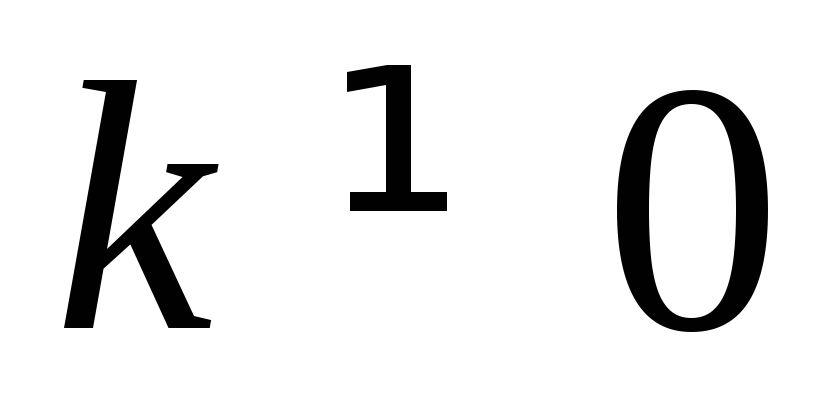 называется отображение плоскости в
себя, при котором каждой точке
называется отображение плоскости в
себя, при котором каждой точке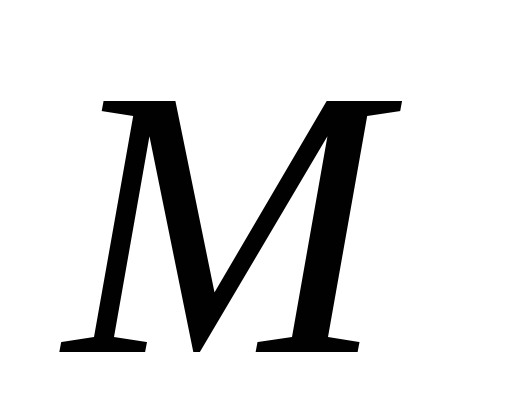 ставится в соответствие точка
ставится в соответствие точка такая, что
такая, что .
.
Проверить, что гомотетия является биективным отображением, а значит, является преобразованием плоскости.
Для
любых двух точек
![]() и их образов
и их образов![]() при гомотетии имеем
при гомотетии имеем![]() .
Тогда
.
Тогда![]() и
и![]() ,
то есть гомотетия с коэффициентом
,
то есть гомотетия с коэффициентом![]() является подобием с коэффициентом
является подобием с коэффициентом![]() .
.
Из
условия
![]() получаемформулы
гомотетии
получаемформулы
гомотетии
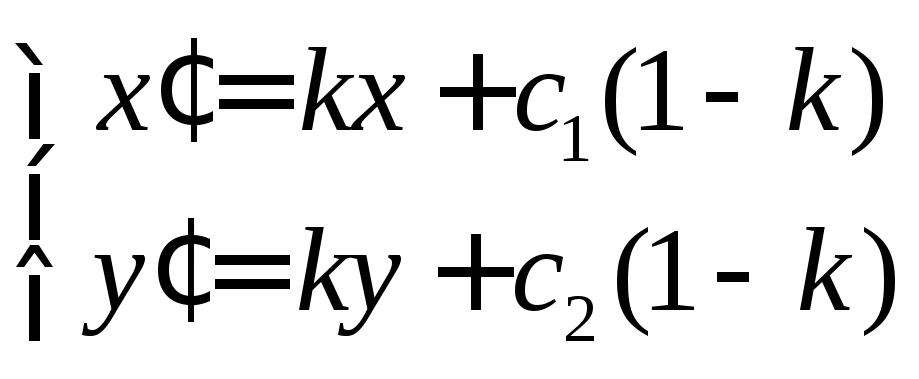 ,
,
позволяющие доказать свойства гомотетии:
При гомотетии прямая, не проходящая через центр гомотетии, переходит в параллельную ей прямую, а прямая, проходящая через центр гомотетии – в себя.
Гомотетия сохраняет простое отношение трех точек прямой, а значит, сохраняет отношение «лежать между» и отрезок переводит в отрезок, луч в луч, угол в угол.
Гомотетия переводит угол в равный угол (Почему?).
Гомотетия сохраняет ориентацию плоскости. Для доказательства этого свойства находим по формулам гомотетии координаты точек, определяющих репер
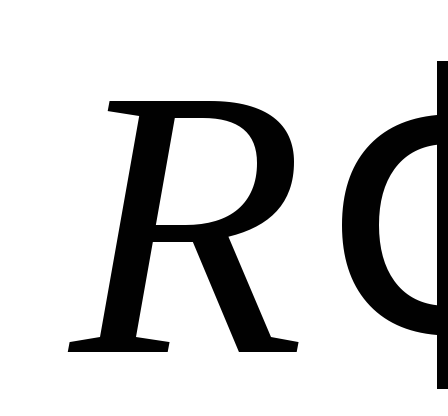 – образ репера
– образ репера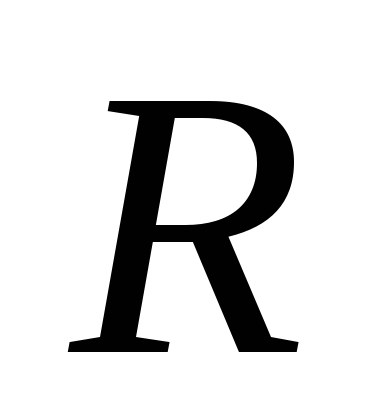 при гомотетии. Затем находим координаты
базисных векторов репера
при гомотетии. Затем находим координаты
базисных векторов репера и убеждаемся, что определитель матрицы
перехода от базиса репера
и убеждаемся, что определитель матрицы
перехода от базиса репера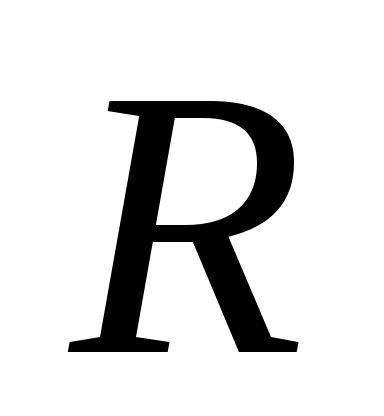 к базису репера
к базису репера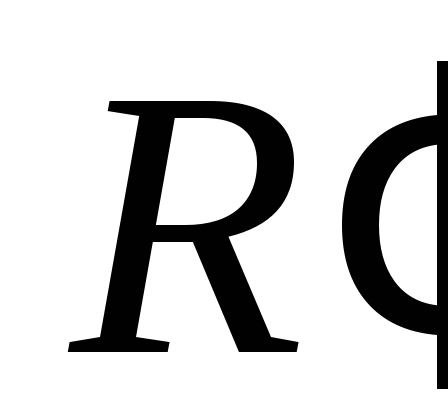 равен
равен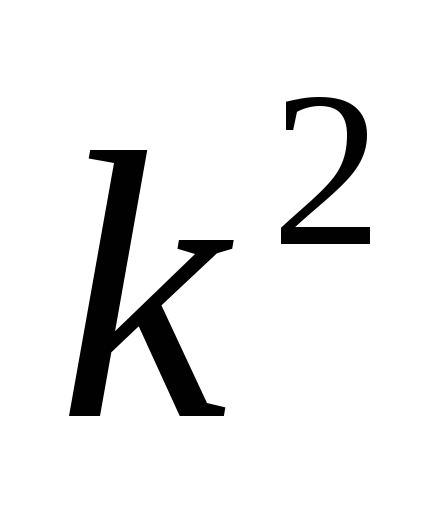 ,
то есть реперы
,
то есть реперы и
и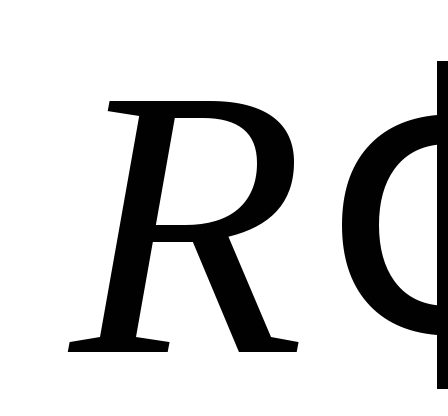 одинаково ориентированы.
одинаково ориентированы.
