Раздел 2. Обработка результатов неравноточных измерений

2.1. Неравноточные измерения и их веса

В практике математической обработки результатов геодезических измерений встречаются случаи, когда приходится анализировать накопленный материал с неодинаковым числом измерений, инструментами разной точности, с различным числом измеряемых величин и различной протяженности, выполненных в разных условиях. Такие измерения можно отнести к неравноточным. Возникает задача определения по результатам неравноточных наблюдений наиболее надежного значения измеряемой величины, оценки точности этих измерений, а также уравнивания различных геодезических сетей.

Достоинство результата измерения, меру его надежности обозначают числом, называемым весом этого измерения, т.е. весом называют степень доверия к результату измерения, выраженную числом.

Чем лучше условия измерения, чем надежнее результат, тем больше его вес, т.е. тем больше наше доверие к нему. Таким образом вес характеризует условия измерения. Но определенным условиям соответствует определенная средняя квадратическая ошибка. Чем меньше средняя квадратическая ошибка, тем надежнее результат, а следовательно, тем больше его вес. Исходя из сказанного, за веса результатов измерений принимают величины обратно пропоциональные квадратам соответствующих им средних квадратических ошибок.

Пусть некоторая величина измерялась неравноточно n раз

x₁, x₂, . . . , x_n;

m₁ , m₂ , . . . , m_n,

тогда веса результатов измерений будут равны

(2.1)

где С - коэффициент пропорциональности, который может быть выбран любым, но одинаковым для данного ряда измерений.

При установлении весов необходимо соблюдать следующие условия: 1) средние квадратические ошибки, по которым определяются веса, должны быть найдены из достаточно большого числа наблюдений;

2) из измерений, по которым вычисляются средние квадратические ошибки, должны быть исключены систематические ошибки.

Cогласно (2.1) при различных значениях С получаем и различные веса, однако соотношение между ними остается неизменным. Отсюда следует, что веса данного ряда измерений являются величинами относительными и их можно одновременно увеличивать или уменьшать в одинаковое число раз.

2.2. Общая арифметическая средина и ее свойства

Пусть дан ряд результатов измерений

x₁ , x₂ , . . . , x_n ;

m₁ , m₂ , . . . , m_n .

Требуется найти наиболее надежное значениеx измеренной величины. Выразим искомую величину в виде линейной функции

(2.2)

где k_i являются некоторой функцией величин m_i и связаны условием

(2.3)

Тогда

(2.4)

Функция приведет нас к надежному результату, если ее средняя квадратическая ошибка будет наименьшей, т. е.

M² = min . (2.5)

Задачу решим по методу Лагранжа

(2.6)

где  - подлежащий определению коэффициент, называемый множителем Лагранжа.

Условие (2.5) определяется точкой экстремума функции Лагранжа .

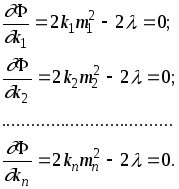(2.7)

Отсюда

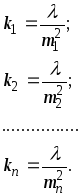(2.8)

Подставив эти значения в уравнение (2.2), получим

(2.9)

Из уравнения (2.8) найдем

(2.10)

С учетом равенства (2.3) определим множитель Лагранжа 

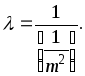(2.11)

Полученное значение  подставим в уравнение (2.9)

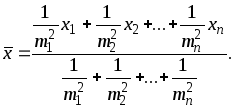(2.12)

Учитывая (2.1), равенство (2.12) можно записать в следующем виде:

(2.13)

Общая арифметическая средина равна сумме произведений каждого неравноточного измерения на его вес, разделенной на сумму весов.

Рассмотрим свойства отклонений от общей арифметической средины. Первое свойство. Алгебраическая сумма произведений отклонений результатов неравноточных измерений от общей арифметической средины на соответствующие веса равна нулю при любом числе наблюдений, т.е.

 pv    . (2.14)

Дан ряд отклонений от арифметической средины с соответствующими весами p_{1 ,} p_{2 , . . . ,} p_n. p₁ v₁ = x₁  x ; p₂ v₂ = x₂  x ; . . . . . . . . . . . . (2.15)

p_n v_n = x_n  x .

Перемножив равенства (2.15) на соответствующие веса и сложив левую и правую части, получим

Cогласно (2.13) будем иметь

следовательно,

(2.16)

Данное свойство можно использовать для контроля вычислений общей арифметической средины.

Второе свойство. Cумма произведений квадратов отклонений результатов неравноточных измерений от общей арифметической средины на соответствующие веса является наименьшей, т.е

[ pvv ] = min (2.17)

Пусть x  x , тогда

(2.18)

Установим связь между отклонениями v и v

(2.19)

В равенстве (2.19) v_i перенесем в правую часть. Затем, умножая на соответствующие веса, возведем в квадрат и почленно сложим

(2.20)

В правой части равенства (2.20) слагаемое 2согласно первому свойству отклонений (2.16). Следовательно, из равенства (2.20) следует, что

(2.21)

Данное свойство подтверждает, что если ошибки результатов неравноточных измерений подчиняются нормальному закону распределения, то наиболее надежным значением является общая арифметическая средина.