1.12. Типовые примеры

1.12.1. Функция произведения непосредственно измеренного аргумента на постоянный коэффициент

Функция имеет следующий вид

(1.50)

где x  величина, измеренная с ошибкой m ;

k  постоянный коэффициент.

Частная производная от функции (1.50) по измеренной величине

Используя равенство (1.47), получим

(1.51)

Cредняя квадратическая ошибка произведения непосредственно измеренной величины на постоянный коэффициент равна произведению этой постоянной на среднюю квадратическую ошибку измеренного аргумента.

1.12.2. Функция линейного вида

Исходная функция представлена следующей зависимостью:

(1.52)

где k_i  некоторые постоянные коэффициенты;

x_i  независимые величины, измеренные со средними квадратическими ошибками m_i.

Находим частные производные функции по независимым аргументам и, подставляя в формулу (1.13), получаем

(1.53)

Если k₁ = k₂ = ... = k_n = 1, то ошибка линейной функции составит

(1.54)

т.е. средняя квадратическая ошибка суммы или разности независимо измеренных величин равна корню квадратному из суммы квадратов ошибок аргументов. Если при этом m₁= m₂ = ...= m_n = 1, то (1.55)

Средняя квадратическая ошибка алгебраической суммы n равноточно измеренных величин в корень квадратный из nраз больше ошибки одного измерения.

Следовательно, накопление ошибок происходит пропорционально корню квадратному из числа измеряемых величин.

1.13. Средняя квадратическая ошибка простой арифметической средины

Дан ряд результатов равноточных измерений одной величины

x_{1 ,} x₂ , . . . , x .

Представим формулу для вычисления простой арифметической средины в виде

x = (1.56)

Согласно (1.47) будем иметь

(1.57)

где m₁ = m₂ = ... = m_n = m . Следовательно, равенство (1.57) примет следующий вид

и окончательно запишем

(1.58)

Итак, средняя квадратическая ошибка простой арифметической средины в корень квадратный раз из числа измерений меньше средней квадратической ошибки одного измерения.

1.14. Формула Бесселя

Выполнив n повторных измерений одной и той же величины, вычислим отклонения результатов этих измерений от арифметической средины

Получим формулу для оценки точности результата измерения через отклонения от арифметической средины, но предварительно рассмотрим свойства отклонений v_i [ 2 ].

Первое свойство. Алгебраическая сумма отклонений результатов равноточных измерений одной и той же величины от простой арифметической средины равна нулю при любом числе измерений. Возьмем ряд отклонений от арифметической средины

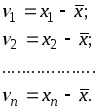( 1.59 )

Суммируя левую и правую части равенства (1.59) , получим

Полученное равенство разделим на n

. (1.60)

Поскольку правая часть равенства (1.60) равна нулю, то и  = 0.

Второе свойство. Сумма квадратов отклонений результатов равноточных измерений от простой арифметической средины меньше суммы квадратов отклонений этих же результатов от любой другой величины, не равной простой арифметической средины, т.е. если x  x , то

[ vv ] < [  ] , (1.61)

где

v_i =x_i - x , _i = x_i - x .

Докажем второе свойство отклонений v_i алгебраическим путем. Вычтем v_i из _i по частям: из правого равенства левое

_i - v_i = x_i - x - x_i + x = x - x = c . (1.62)

Для n числа наблюдений получим ряд отклонений _i

_ v_  c 

_ v_  c  (1.63)

. . . . . . . . .

_n  v_n  c .

Возведем в квадрат равенства (1.63) и, суммируя левую и правую части, получим

[  ] = [ vv ] + nc² + 2c [ v ] . (1.64)

Но член 2c [ v ] = 0 по первому свойству отклонений v_i , тогда

[  ] = [ vv ] + nc² . (1.65)

Из формулы (1.65) следует, что

[  ] > [ vv ]

на положительное число nc² , вне зависимости от того, x большеx, или меньше. Таким образом, при x  x

[ vv ] < [  ], (1.66)

что и требовалось доказать.

Для решения поставленной в начале данного параграфа задачи определим связь между истинными ошибками  _i и отклонениями v_i . Напишем

_i =x_i - X ; v_i = x_i - .

Cоставим разность

. (1.67)

Возведем в квадрат равенства (1.67) и почленно просуммируем

. (1.68)

Согласно первому свойству отклонений имеем

. (1.69)

В равенстве (1.69) левая часть согласно формуле Гаусса равна

. (1.70)

Разность данного равенства соответствует средней квадратической ошибке значения среднего арифметического из результатов измерений, т.е. равнаМ. Тогда с учетом вышеизложенного получим вместо равенства (1.69) следующее

или

.

Откуда средняя квадратическая ошибка результата измерения составит

. (1.71)

Средняя квадратическая ошибка вычисления ошибки согласно формуле (1.71) равна

. (1.72)