2.5. Вычисление ошибки единицы веса

2.5.1. Вычисление ошибки единицы веса при

установлении весов по известным средним

квадратическим ошибкам

Согласно (2.22) и (2.26) имеем

откуда (2.40)

Если при этом известны веса, то ошибку единицы веса можно вычислить по формуле

(2.41)

2.5.2. Вычисление ошибки единицы веса

через истинные ошибки

Дан ряд неравноточных измерений

x₁ , x_{2 , . . . ,} x_n (2.42)

с соответствующими истинными ошибками, весами и средними квадратическими ошибками

₁ , ₂ , . . . , _n ; (2.43) p_{1 ,} p₂ , . . . , p_n ; (2.44) m₁ , m₂, . . . , m_n . (2.45)

Умножим каждый результат ряда (2.42) на получим новый ряд

(2.46)

При увеличении или уменьшении значения x в произвольное число раз изменяются и истинные ошибки в соответствующее число раз

(2.47)

Соответственно

(2.48)

а это согласно (2.41)

(2.49)

Откуда следует, что ряд (2.46) является равноточным со средней квадратической ошибкой  и истинными ошибками (2.47), тогда, использовав формулу Гаусса (1.13), получим

(2.50)

Надежность определения  вычислится

(2.51)

2.5.3. Вычисление средней квадратической ошибки измерения углов в триангуляции

Даны невязки в треугольниках

w₁ , w₂ , . . . , w_n ,

причем

(2.52)

Считая углы равноточно измеренными с весом 1, находим вес p_i функции _i

или p_i =

Так как невязки являются истинными ошибками, воспользуемся формулой (2.50)

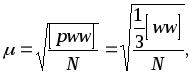
где N - число треугольников сети триангуляции.

Окончательно имеем

(2.53)

Формула (2.53) носит название формулы Ферреро.

2.5.4. Вычисление ошибки единицы веса через отклонения от арифметической средины

Пусть даны результаты неравноточных измерений

x₁ , x₂ , . . . ,x_n ;

p₁ , p₂ , . . . , p_n ,

а также известны истинное значение X и среднее арифметическое x₀. Составим два ряда истинных ошибок и отклонений от арифметической средины

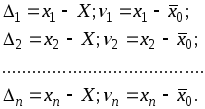(2.54)

Из первого ряда вычтем второй, в результате чего получим

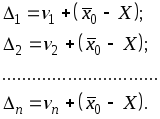(2.55)

Равенства (2.55) возведем в квадрат и умножим на соответствующие веса. Полученные равенства почленно просуммируем и в результате будем иметь

(2.56)

В правой части равенства (2.56) второе слагаемое согласно первому свойству отклонений от общей арифметической средины равно нулю. Cледовательно,

(2.57)

Cогласно (2.50) имеем , а выражение в круглых скобках является средней квадратической ошибкой среднего значения, т.е.

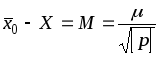(2.58)

или (2.59)

С учетом (2.58) и (2.59) равенство (2.57) примет вид

или

Откуда

(2.60)

Надежность определения  вычислится

. (2.61)