ò

æ

¶u

ö

òò

éæ ¶u ö2

æ

¶u ö2 ù

= -

çϕ(x, y)

dS ÷ +

êç

÷

ç

÷

(6.7.27)

¶n

+ ç

÷ ú dxdy .

∂G

è

ø

G êè

¶x ø

è

¶y ø ú

ë

û

Подставляя (6.7.26) и (6.7.27) в формулу (6.7.25), будем иметь

2

òò

éæ ¶u ö2

æ

¶u ö2

ù

ò

æ

¶z

ö

êç

÷

ç

÷

- 2 fuúdxdy -

çϕ(x, y)

dS ÷ .

(6.7.28)

F [u] =

+ ç

÷

¶n

G

êè

¶x ø

è

¶y ø

ú

∂G è

ø

ë

û

Так как

последнее

слагаемое

в

формуле

(6.7.28)

не

зависит от

функции u , то краевая задача (6.7.13) – (6.7.14) эквивалентна вариационной

задаче для функционала

	òò	éæ ¶u ö2		æ	¶u ö2	ù	(6.7.29)
F[u]=		êç	÷	ç	÷	- 2 fuú dx dy
				+ ç	÷
	G	êè	¶x ø	è	¶y ø	ú
в классе функций Ξ1 .		ë				û
		f = f (x, y) ≡ 0,
В частном случае, если						то получаем уравнение Лапласа

u = 0, причём краевая задача (6.7.13) – (6.7.14) есть известная задача Дирихле. Решением этой задачи, как вытекает из формулы (6.7.29), является функция u

из		класса			Ξ1 ,		минимизирующая	интеграл	Дирихле
	òò	éæ ¶u ö2		æ	¶u ö2 ù
F[u] =		êç	÷	ç	÷	údxdy .	Убедиться в этом	самостоятельно,	выписав
				+ ç	÷
	G	êè	¶x ø	è	¶y ø	ú
		ë				û

уравнение Остроградского для данного функционала.

ИСТОРИЧЕСКАЯ СПРАВКА

Галёркин Борис Григорьевич (1871 – 1945) – выдающийся русский советский математик и инженер. Специалист в области теории упругости. Родился в Полоцке. В 1899 г. окончил Петербургский технологический институт. В 1928 г. Борис Григорьевич был избран членом-корреспондентом, а в 1935 г. действительным членом Академии Наук СССР. Труды Б.Г.Галеркина относятся к проблемам строительной механики и теории упругости. Разработал методы решения дифференциальных уравнений теории упругости. С его именем неразрывно связан метод конечных элементов, применяемый

для численного решения дифференциальных уравнений в частных производных. Предложенная Б. Г. Галёркиным

формула решения уравнений уп-ругого равновесия, содержащая три бигармонические функции, позволила эффективно решить многие пространственные задачи теории упругости. Б. Г. Галёркин – один из создателей теории изгиба упругих пластин.

§8. Метод Ритца численного решения вариационной задачи

Рассмотрим следующий прямой метод приближенного решения вариационной задачи. Выберем функционал следующего вида: F[u] = (Lu,u) − 2( f ,u) , который определим на некотором линейном множестве

114

Ξ = {u}, где L – положительно-определенный линейный оператор; f –

заданная непрерывная функция. Предполагается, что функции класса Ξ удовлетворяют условиям R[u] = ϕ (P) , где R – известный линейный

функционал; ϕ – заданная функция. Построим последовательность достаточно гладких линейно независимых функций u0 (P), u1(P), K, un (P) , где u0 (P) удовлетворяет неоднородным краевым условиям R[u0 ] = ϕ (P) , а функции ui (P), i = 1, 2,K, n – однородным краевым условиям R[ui ] = 0, i =1, 2,K, n . Составим следующую линейную комбинацию:

u(P; c1, c2,

n

Так как R[u] = R[u0 ] + åci ×0 = ϕ

i=1

n

K, cn ) = u0 (P) + åciui (P) . (6.8.1)

i=1

(P), то u Ξ при любых постоянных

c1, c2,K, cn . Приближенное решение нашей вариационной задачи будем искать в виде (6.8.1). Для этого подставляем u(P; c1, c2,K, cn ) в выбранный функционал F[u] = (Lu,u) − 2( f ,u) и получаем

	F[u]= (c1 ,c2 ,K,cn ) ,	(6.8.2)
где	– известная функция, зависящая от n	переменных c1, c2,K, cn .

Подсчитываем коэффициенты c1, c2,K, cn таким образом, чтобы значение F [u] было минимальным. Это приводит к решению следующей системы уравнений:

	∂	=0,	∂	=0,...,	∂	=0.	Таким образом,	вариационная	задача приближенно
	∂c1		∂c2
				∂cn
сводится				к	задаче		об отыскании	безусловного	экстремума функции

(c1, c2 , K, cn ) .

Рассмотрим приведенную выше схему применительно к решению задачи

Дирихле для уравнений Лапласа:
u = 0, (x, y) G	(6.8.3)
u |∂G = f (x, y) ,	(6.8.4)

где ∂G – простой замкнутый контур, ограничивающий конечную область G , a

функция f (x, y) непрерывна на	∂G .		Данная		краевая задача		эквивалентна
следующей вариационной задаче для функционала:						ö2 ù
F[y] =	òò	éæ	¶u ö2	æ	¶u		(6.8.5)
		êç	÷	ç		÷
				+ ç	¶y	÷ ú dxdy ,
	G êè		¶x ø	è		ø ú
		ë				û

в классе функций, имеющих непрерывные частные производные до второго порядка включительно в замкнутой области G + ∂G и удовлетворяющих на границе ∂G краевому условию (6.8.4). Построим конечную систему линейно

независимых функций			(которые называются координатными		функциями)
u (x, y),	u (x, y), ...,	u	n	(x, y) C(2) (G + ∂G) , которые должны удовлетворять
0	1
условия на границе u0 (x, y) |∂G = f (x, y), ui (x, y) |∂G = 0, (i =1, 2,					..., n). Тогда
					115

линейная

комбинация

ϕ(x, y) = u0

n

принадлежит

классу

+ åciui (x, y) ,

i=1

допустимых функций при любых постоянных c1, c2,K, cn . Более коротко:

n

ϕ(x, y) = åciui (x, y),

(6.8.6)

i=0

где c0 = 1. Подставляя выражение (6.8.6) в функционал (6.8.5), получим

F [ϕ] = òò

n

∂ui )2

n

∂ui )2

[(åci

+ (åci

] dxdy .

(6.8.7)

G

i=0

∂x

i=0

∂y

Подберем коэффициенты c1, c2,K, cn так, чтобы функция

F [ϕ]

имела

минимум. Для этого требуется выполнение условий

∂

n

∂u j

∂u j

n

∂u j

∂u j

F[ϕ] = 2

òò[(åci

)

+ (åci

)

] dxdy = 0 , j

=1, 2, ...,

n ,

(6.8.8)

∂с j

∂x

∂x

∂y

∂y

G

i=0

i=0

что приводит к решению системы следующих алгебраических уравнений:

∂u

где [ui ,u j ] = òòG ( ∂xi

ì[u

0

,u ]+c [u ,u ]+...+c

n

[u

n

,u ] =0,

ï

1

1

1 1

1

ï[u0,u2 ]+c1[u1,u2 ]+...+cn[un ,u2 ] =0,

í

.....................................................

ï

ï[u

0

,u

n

]+c [u ,u

n

]+...+c

n

[u

n

,u

n

]=0,

î

1

1

∂u j

+

∂ui

∂u j

)dxdy

причем [ui ,u j ] = [u j ,ui ] .

∂x

∂y

∂y

(6.8.9)

Из линейной

системы (6.8.9) определяются коэффициенты c1, c2,K, cn .		Функция ϕ (x, y) и
будет	являться приближенным решением задачи	Дирихле. Точность

приближения зависит от выбора координатных функций uk (x, y) и от числа этих функций.

ИСТОРИЧЕСКАЯ СПРАВКА

Ритц Вальтер (Ritz Walter) (1878 – 1909) – знаменитый немецкий математик и физик-теоретик. Основные исследования

относятся к решению вариационных задач математической физики. Открыл спектральную формулу (формула Ритца).

Разработал идею вычисления частот непосредственно из энергетического функционала, без решения дифференциальных уравнений. Предложил (1908) мощный прямой метод приближенного решения вариационных задач – метод Ритца. Метод нашел широкое применение в теории колебаний, теории упругости, инженерной механике. Этот метод применяется для

приближённого решения вариационных задач и тех краевых задач математической физики, которые сводятся к вариационным. Строгое теоретическое обоснование метода Ритца дал в 1918 г. известный русский математик И. М. Крылов.

116

Пример. Найти функцию u = u(x, y), гармоническую в области G : x > 0, y > 0, x + y < 1 и удовлетворяющую на границе ∂G : x = 0, y = 0, x + y = 1 условию u | ∂G = x2 + y2 .

Решение. Выберем следующую систему координатных функций: u0 (x, y) = x2 + y2 , u1(x, y) = xy(1− x − y) ,

u2 (x, y) = x2 y(1− x − y) , u3(x, y)= xy2 (1−x− y)K

и составим линейную комбинацию

ϕ(x, y) = x2 + y2 + c1xy(1− x − y) + c2x2 y(1− x − y) + c3xy2 (1− x − y) . (6.8.10)

Легко проверить, что функция ϕ (x, y) удовлетворяет краевому условию ϕ | ∂G = x2 + y2 при любых значениях постоянных c1, c2, c3 .

Для составления системы (6.8.9) подсчитываем коэффициенты при неизвестных c1, c2, c3 и свободные члены:

[u0,u1] = [u1,u0 ] = òò[2x(y − 2xy − y2 + 2y(x − x2 − 2xy)]dxdy,

G

[u0,u2 ] = [u2,u0 ] = òò[2x(2xy − 3x2 y − 2xy2 ) + 2y(x2 − x3 − 2x2 y)]dxdy,

G

[u0 ,u3 ] = [u3 ,u0 ] = òò[2x( y2 − 2xy2 − y3 ) + 2y(2xy − 2x2 y − 3xy2 )]dxdy,

G

[u1,u1] = òò[(y − 2xy − y2 )2 + (x − x2 − 2xy)2 ]dxdy,

G

[u1,u2 ] = [u2 ,u1] = òò[(y − 2xy − y2 )(2xy − 3x2 y − 2xy2 ) +(x − x2 − 2xy)(x2 − x3 − 2x2 y)]dxdy,

G

[u1,u3 ] = [u3 ,u1] = òò[(y − 2xy − y2 )(y2 − 2xy2 − y3 ) +(x − x2 − 2xy)(2xy − 2x2 y − 3xy2 )]dxdy,

G

[u2 ,u2 ] = òò(2xy − 3x2 y − 2xy2 )2 + (x2 − x3 − 2x2 y)2 ]dxdy,

G

[u2 ,u3] = [u3,u2 ] = òò[(2xy − 3x2 y − 2xy2 )( y2 − 2xy2 − y3) +

G

+ (x2 − x3 − 2x2 y)(2xy − 2x2 y − 3xy2 ]dxdy,

[u3,u3] = òò[( y2	− 2xy2 − y3)2 + (2xy − 2x2 y − 3xy2 )2 ]dxdy.
G	= [u1,u1], a12 = [u1,u2 ], a13 = [u1,u3 ], a21 = [u2 ,u1],
Введём обозначения a11

a22 = [u2 ,u2 ], a23 = [u2 ,u3 ], a31 = [u3,u1] , a32 = [u3 ,u2 ], a33 = [u3 ,u3 ], b1 = [u0 ,u1],

b2 = [u0 ,u2 ],

b3 = [u0 ,u3 ].

Получаем

следующую

систему линейных

алгебраических

уравнений

(СЛАУ):

A × C = B , где

A = [ai j ,i =

1,3, j = 1,3] ,

C = [c ,c

2

,c

]T , B = [b ,b

2

,b ]T .

1

3

1

3

117

Значения коэффициентов при неизвестных c1, c2, c3 считает следующий

скрипт MatLab:

1.% подсчет коэффициентов при координатных функциях

2.syms x y u k;

3.% u(1),u(2),u(3),u(4) - система координатных функций

4.u(1) = x^2+y^2; u(2) = x*y*(1-x-y);

5.u(3) = x^2*y*(1-x-y); u(4) = x*y^2*(1-x-y);

6.% k - таблица коэффициентов при неизвестных

7.for i=1:4

8.for j=i:4

9.% k(j,i) = k(i,j) - элемент таблицы

10.k(j,i)=int(int(diff(u(i),'x')*diff(u(j),'x')+diff(u(i),'y')*diff(u(j),'y'),'y',0,1-x),'x',0,1);

11.k(i,j) = k(j,i);

12.end; end;

13.disp('Значения коэффициентов при неизвестных:');

14.disp(k);

Решив	систему,	находим	c1 ≈ 4,6667;	c2 = c3 ≈ −2,3333.	Подставляя
найденные	значения	величин	c1, c2, c3 в	формулу (6.8.9)	и получаем

приближенное формульное решение нашей задачи:

ϕ(x, y) = x2 + y2 + xy(1− x − y)[4,6667 − 2,3333(x + y)].

Следующий скрипт MatLab визуализирует полученное методом Ритца решение:

%визуализация решения, полученного методом Ритца

1.clear all;

2.format long;

3.x=[0:.02:1];

4.y=[0:.02:1];

5.[X,Y]=meshgrid(x,y); % задаём сетку

6.for i=1:length(x)

7.for j=1:length(y)

8.if (y(j)<=1-x(i)) % вычисляем значения, которые попадают в заданную область

9.Z(i,j)=x(i).^2+y(j).^2+x(i)*y(j)*(1-x(i)-y(j))...

10.*(4.6667-2.3333*(x(i)+y(j)));

11.else

12.Z(i,j)=NaN;

13.end; end; end;

14.surf(X,Y,Z); % визуализируем решение

15.title ('\bfRitc method') % заголовок графика

16.xlabel('x'); ylabel('y'); zlabel('z(x,y)'); v = axis; % границы осей

17.da = daspect; % масштаб осей

18.da(1:2) = min(da(1:2)); % min из двух

19.daspect(da) % выравняли масштаб осей

20.axis(v); % оставили границы

21.colormap(gray) % выбрали палитру

22.grid on % показали сетку

23.box on % показали внешний контур

118

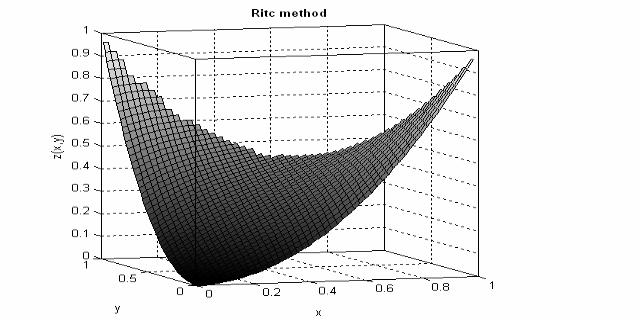
График полученного решения совпадает с графиком, приведенным в §4:

119

Глава 6. Линейные эллиптические дифференциальные уравнения второго порядка в частных производных

ОПЕРАТОР ЛАПЛАСА В КРИВОЛИНЕЙНЫХ СИСТЕМАХ КООРДИНАТ. ТИПЫ КРАЕВЫХ ЗАДАЧ ДЛЯ ОПЕРАТОРА ЛАПЛАСА. КОРРЕКТНОСТЬ ЗАДАЧ ДЛЯ ОПЕРАТОРА ЛАПЛАСА. ПОСТРОЕНИЕ РЕШЕНИЯ ВНУТРЕННЕЙ ЗАДАЧИ ДИРИХЛЕ НА КРУГЕ. АНАЛИЗ РЕШЕНИЯ ЗАДАЧИ ДИРИХЛЕ. ИНТЕГРАЛЬНАЯ ФОРМУЛА ПУАССОНА. ОСНОВЫ ВАРИАЦИОННОГО МЕТОДА РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ. МЕТОД РИТЦА ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ ДИРИХЛЕ.

§1. Оператор Лапласа в криволинейных системах координат

Выпишем оператор Лапласа в R2 в декартовой прямоугольной системе координат:

Du =	¶2u	+	¶2u.	(6.1.1)
	¶x2		¶y2

Выпишем параболические, гиперболические и эллиптические уравнения общего вида, используя дифференциальные операторы первого порядка.

Градиент: grad = (¶∂x , ¶∂y , ¶∂z ). Дивергенция: div = ¶∂x + ¶∂y + ¶∂z . Ротор:

	i		j
rot a =	¶	¶
	¶x		¶y
	ax		a y

k

¶¶z = [a = az

æ	¶a	z		¶a y ö
ç			-		÷
(ax ,a y ,az )]=ç	¶y			¶z	÷ i
è					ø

+æ ¶az - ¶ax ö ç ÷ j è ¶x ¶z ø

æ ¶a y			¶a	x	ö
ç		-			÷
+ç	¶x		¶y		÷k.
è					ø

Параболическое уравнение примет вид: α ×ut/ - div(β × grad(u)) + γ ×u = f , где α,β ,γ – некоторые известные функции из R; гиперболическое уравнение будет иметь вид: α ×utt′′- div(β × grad(u)) + γ ×u = f , где α,β ,γ – некоторые известные функции из R; эллиптическое уравнение: - div(β × grad(u)) + γ ×u = f ,

где β ,γ – некоторые известные функции из R. Оператор задачи

Штурма –

Лиувилля

примет

вид

- div(β × grad(u)) + γ ×u = α ×λu,

где

α,β ,γ

–

коэффициенты.

В приложениях важную роль играет набла Ñ– оператор Гамильтона. Он

вводится либо как

символический

вектор

Ñ =

∂

i +

∂

j +

∂

k ,

либо

как

¶y

¶z

¶x

дифференциальный

оператор:

æ

¶u

, ¶u ,

¶u

ö

В

физических

Ñu = grad u = ç

÷.

ç

¶x

¶y

¶z

÷

è

ø

приложениях часто применяется следующая запись: grad u = Ñu;

div a = (Ñ,a);

rot(a)=[Ñ,a].

Выпишем оператор Лапласа

в двумерном случае в полярной системе

координат.

Напомним,

что

переход из

полярных

координат R2

в

прямоугольные декартовы задается соотношениями: x= ρcosϕ , y = ρsinϕ . Переход из декартовых координат R2 в полярные задается соотношениями:

95

ρ =

ϕ = arctg

y

.

x2 + y2

,

Вычисляем

полную

производную:

∂u

∂u

∂ρ

∂u

∂ϕ

x

=

×

+

×

.

¶x

¶x

¶ϕ

¶ρ

¶x

Подсчитываем:

∂ρ = (

)

¢

1

x

=

ρ cosϕ

= cosϕ ,

x2 + y2

=

× 2x =

¶x

x

2 x2 + y2

x2 + y2

ρ

¶ϕ

æ

y

ö

¢

1

æ

y ö

1

æ

ρsinϕ

ö

æ

sinϕ

ö

sinϕ

= çarctg

÷

=

×ç-

÷

=

ç-

÷ = cos2

ϕç-

÷ = -

.

¶x

x

2

x

2

2

ρ

2

2

2

ϕ

ρ

è

øx

1+

æ y ö

è

ø

1

+tg ϕ è

cos

ϕ ø

è

ρ cos

ø

ç

÷

è x ø

Получаем

∂u

=

∂u

× cosϕ -

∂u

×

sinϕ

.

¶x

¶ϕ

¶ρ

ρ

Вычисляем полную производную

∂u

=

∂u

×

∂ρ

+

∂u

×

∂ϕ

. Подсчитываем:

¶y

¶ρ

¶y

¶y

¶ϕ

∂ρ = (

)

¢

1

y

=

ρ sinϕ

= sinϕ ,

x2 + y

2

=

× 2y =

¶y

y

2 x2 + y2

x2 + y2

ρ

¶ϕ

æ

y

ö ¢

1

1

1

1

= cos2

ϕ ×

1

cosϕ

= çarctg

÷

=

×

=

×

=

.

¶y

x

æ y

ö2

x

ρ cosϕ

ρ cosϕ

ρ

è

øy

2

1

+

ç

÷

1+ tg

ϕ

è x

ø

Получаем

∂u

=

∂u

×sinϕ +

∂u

×

cosϕ

.

¶y

¶ϕ

¶ρ

ρ

Теперь вычислим вторую производную

¶2u

. Введем обозначение

¶x2

∂u

¶2u

¶ρ

¶ϕ

F =

d æ ¶u

ö

¶F

¶F

¶F

, тогда

¶x2

=

ç

÷

=

1

=

1

×

+

1

×

,

¶x

¶x

¶x

¶ϕ

¶x

1

dx è ¶x

ø

¶ρ

¶F

æ

¶u

× cosϕ -

¶u

sinϕ

ö

¢

¶2u

×cosϕ -

æ

¶2u

sinϕ

¶u

sinϕ

ö

1

= ç

×

÷

=

ç

×

-

×

÷,

2

2

¶ρ

è ¶ρ

¶ϕ ρ ø

ρ

¶ρ

ç

¶ϕ¶ρ ρ

¶ϕ ρ

÷

è

ø

¶F

æ ¶u

×cosϕ -

¶u

sinϕ ö ¢

æ

¶2u

×cosϕ -

¶u

×sinϕ

ö

æ

¶2u sinϕ

¶u

cosϕ ö

1

ç

÷

ç

÷

=ç

×

÷

=

2 ×

+

×

¶ϕ

¶ϕ

ρ

ç

¶ρ¶ϕ

¶ρ

÷

-ç

¶ϕ

ρ

¶ϕ

ρ

÷.

è ¶ρ

ø

è

ø è

ø

ϕ

Получаем

¶2u = ¶2u ×cos2 ϕ - ¶x2 ¶ρ2

+	¶2u	×	sin2	ϕ	+	¶u
	¶ϕ 2		ρ 2			¶ϕ

¶2u

×

sinϕ cosϕ

+

¶u

×

sinϕ cosϕ

-

¶2u

×

cosϕsinϕ

+

¶u

×

sin2 ϕ

+

¶ϕ¶ρ

ρ

¶ϕ

ρ2

¶ρ¶ϕ

ρ

¶ρ

ρ

×cosϕ sinϕ .

ρ2

96

Теперь вычислим вторую производную

¶2u

.

Введем обозначение

¶y2

∂u

¶2u

d

æ

¶u

ö

¶F

¶F

¶ρ

¶F

¶ϕ

F =

, тогда

2

=

ç

÷ =

2

=

2

×

+

2

×

,

2

¶y

¶y

dy

ç

¶y

÷

¶y

¶ρ ¶y ¶ϕ ¶y

è

ø

¶F

æ

¶u

×sinϕ +

¶u

cosϕ

ö

¢

¶2u

×sinϕ +

æ

¶2u

cosϕ

¶u

cosϕ

ö

2

=

ç

×

÷

=

ç

×

-

×

÷,

2

2

¶ρ

è ¶ρ

¶ϕ ρ

øρ

¶ρ

ç

¶ϕ¶ρ ρ

¶ϕ ρ

÷

è

ø

¶F

æ ¶u

¶u

cosϕ ö ¢

æ

¶2u

¶u

ö

æ

¶2u

cosϕ

¶u

sinϕ ö

2

ç

÷

ç

÷

= ç

×sinϕ +

×

÷

=

×sinϕ +

×cosϕ

2 ×

-

×

¶ϕ

¶ϕ

ρ

ç

¶ρ¶ϕ

¶ρ

÷ +ç

¶ϕ

ρ

¶ϕ

ρ

÷.

è¶ρ

ø

è

ø è

ø

Получаем

ϕ

cosϕsinϕ

cosϕsinϕ

sinϕcosϕ

cos2 ϕ

¶2u

=

¶2u

×sin2 ϕ +

¶2u

×

-

¶u

×

+

¶2u

×

+

¶u

×

+

¶y2

¶ρ2

¶ϕ¶ρ

¶ϕ

¶ρ¶ϕ

ρ

ρ2

ρ

¶ρ ρ

+

¶2u

×

cos2 ϕ

-

¶u

×

sinϕ cosϕ

.

¶ϕ2

ρ 2

¶ϕ

ρ 2

Подставляя и приводя подобные, окончательно получаем

Du =

¶2u

+

1

×

¶u

+

1

×

¶2u

.

(6.1.2)

¶ρ 2

ρ

¶ρ

ρ 2

¶ϕ 2

Замечание. Самостоятельно получить запись оператора Лапласа в

R3 в

цилиндрической и сферической системах координат соответственно:

Du =

¶2u

+

1

×

¶u

+

1

×

¶2u

+

¶2u

,

¶ρ 2

¶ϕ2

¶z2

ρ ¶ρ ρ 2

Du =

¶2u

+

¶u

×

2

+

¶2u

×

1

+

¶u

×

cosθ

+

¶2u

×

1

.

¶ρ 2

¶ρ

ρ

¶ϕ 2

ρ 2 sin 2 θ

¶θ

ρ 2 sinθ

¶θ 2

ρ 2

§2. Типы краевых задач для оператора Лапласа

Задача Дирихле: краевая задача с граничным условием 1-го рода

Условие Дирихле: на границе области задана некоторая функция. Внутренняя задача Дирихле:

	ì	¶	2	u		1
	ïDu =				+
		¶ρ 2				ρ
	í
	ï			u(1,ϕ
	î

	×	¶u	+	1	×	¶2u	=0,ρÎ[0,1],	(6.2.1)
		¶ρ		ρ 2		¶ϕ 2
	)= g(ϕ),ϕÎ[0,2π ].

Помимо внутренней задачи Дирихле можно рассмотреть следующую задачу Дирихле, которая носит название внешней задачи Дирихле:

ì

¶

2

u

1

¶u

1

¶

2

u

=0, ρ ³1,

ïDu =

+

×

+

×

(6.2.2)

¶ρ2

ρ 2

¶ϕ2

í

ρ ¶ρ

ï

u(1,ϕ)= g(ϕ),ϕÎ[0,2π ].

î

97

Задачу Дирихле можно рассматривать и на кольце:

ì

¶

2

u

1

¶u

1

¶

2

u

=0,a£ρ £b,

ïDu =

+

×

+

×

¶ρ2

ρ 2

¶ϕ2

ï

ρ ¶ρ

ï

(ϕ),

(6.2.3)

íu(a,ϕ)= g1

ïu(b,κ)= g

2

(ϕ),ϕÎ[0,2π ].

ï

ï

î

Задача Неймана: краевая задача с граничным условием 2-го рода

Для данной краевой задачи на границе области задается производная по внешней нормали ∂∂un . Эта производная эквивалентна вытекающему потоку,

т.е. через границу области задан поток.

Постановка задачи Неймана в декартовой системе координат:

ì

¶

2

u

2

u =0,

ïDu =

+ ¶

ï

¶x

2

¶y

2

(6.2.4)

í

¶u

ï

= g(x,y).

ï

¶n

î

∂G

Пример постановки задачи Неймана в полярной системе координат на

круге:

ì

2

u

1

¶u

1

¶

2

u

ïDu =

¶

+

×

+

×

=0,ρÎ[0,1],ϕÎ[0,2π

];

¶ρ2

ρ 2

ï

ρ ¶ρ

¶ϕ2

(6.2.5)

í

¶u

= g(ϕ),ρ =1,ϕÎ[0,2π ].

ï

ï

¶n

î

∂G

Отметим, что

для

данной

задачи поток тепла направлен внутрь при

ϕ = [0,π ] и наружу при ϕ [π ,2π ].

Отдельно отметим, что задача Неймана для уравнения Лапласа имеет физический смысл только в том случае, когда суммарный поток тепла через границу области равен нулю. На границе должно выполняться соотношение

ò ∂u dS = 0 . В противном случае задача не имеет физического смысла, хотя

∂G ∂n

может иметь математическое решение.

Краевая задача с граничным условием 3-го рода

Рассмотрим задачу с граничным условием смешанного типа. Граничное

условие получено как линейная суперпозиция двух первых типов граничных

условий и имеет следующий вид:	∂u			= −h(u − g) . Здесь u(x, y)	– искомая
	∂n		∂G
функция; g(x, y) – некоторая заданная на границе функция; h –					некоторая

константа, дифференцирование проводится по внешней нормали к ∂G .

Согласно этому условию, поток тепла, втекающий в область через границу, пропорционален разности между искомой температурой u и некоторой заданной температурой g . Это означает при k > 0 следующее. Если

98

температура u на границе области выше температуры окружающей среды, то тепло вытекает из области. Если температура u на границе соответственно ниже температуры окружающей среды, то тепло втекает в область.

Это закон теплообмена Ньютона, записанный в производных для стационарной задачи теплообмена.

Если рассмотреть процесс во времени, то получится не стационарное, а

эволюционное уравнение параболического типа ∂∂ut + u = 0 . Поэтому, как

отмечалось ранее, эллиптическое уравнение является стационарным случаем (мгновенным срезом в некоторый момент времени) параболического уравнения.

§3. Корректность задач для оператора Лапласа

Задачи математической физики делятся на корректно и не корректно поставленные. Данному понятию предпошлём понятие устойчивости.

Решение краевой задачи называется устойчивым, если для каждого действительного числа ε > 0 найдется такое действительное число δ (ε ) > 0 , что

при изменении исходных данных задачи на величину по норме, не превосходящей δ , решение задачи в каждой точке внутри области и на границе получит приращение по норме, не превосходящее ε .

Краевая задача поставлена корректно в рассмотренной области, если её решение: существует, единственно, устойчиво.

Задачи, не удовлетворяющие хотя бы одному из этих требований, называются не корректно поставленными.

Пример Адамара. Покажем, что следующая задача Коши для уравнения Лапласа поставлена не корректно:

u =

∂2u +

∂2u

= 0, íìu(x,0)= f (x),

∂x2

∂y2

îu¢y (x,0)= F(x); -¥< x<+¥.

Положим:

f (x) = 0;

F (x) =

1

sin(ax). Тогда решение запишется в виде:

1

1

a

1

1

(ea y -e−a y ).

u (x, y)=

sin(ax)×

Положим

теперь f (x) = 0, F (x) = 0. Тогда

1

a2

2

2

2

решение:

u2 (x, y) = 0.

Теперь

оценим

отклонение

начальных данных и

отклонение получившихся решений:

= 1

Sup

f

1

(x) − f

2

(x)

= 0;

Sup

F (x) − F (x)

;

x

x

1

2

a

u (x, y)−u

1

sin(ax)(ea y −e−a y )

=

1

(ea y −e−a y ).

Sup

2

(x,y)

= Sup

x,y³0

1

x,y³0

2a2

2a2

99

Отсюда следует, что при сколь угодно малом отклонении начального условия α , отклонения соответствующих решений могут быть сколь угодно велики. Задача не обладает свойством устойчивости. Задача является не корректно поставленной.

§4. Схема решения внутренней задачи Дирихле на круге

Рассмотрим следующую задачу Дирихле на круге:

ì

¶

2

u

1

¶u

1

¶

2

u

= 0, ρ Î[0;1]

ïDu =

+

×

+

×

(6.4.1)

¶ρ2

ρ

¶ρ

í

ρ2

¶ϕ2

ï

u(1,ϕ) = g(ϕ); ϕ Î[0,2π ] .

î

I этап. Будем искать решение методом разделения переменных, полагая

u(ρ,ϕ) = F (ϕ) × R(ρ) ,

(6.4.2)

Подставляя (6.4.2) в уравнение (6.4.1) , получим

¢¢

1

¢

1

¢¢

,

ρ2

F(ϕ) × R (ρ) + ρ

×F(ϕ) × R (ρ) +

×F (ϕ) × R(ρ) = 0

или

ρ

2

¢¢

¢¢

¢

F (ϕ) = -

× R

(ρ) + ρ × R (ρ)

.

(6.4.3)

F(ϕ)

R (ρ)

В силу независимости правой и левой частей (6.4.3) друг от друга, приравниваем их к некоторой константе μ и получаем следующую систему

двух линейных однородных дифференциальных уравнений:
			¢¢								(6.4.4)
		F		(ϕ) - μ ×F(ϕ) = 0,
		ρ	2	¢¢	¢						(6.4.5)
				× R (ρ) + ρ × R (ρ) + μ × R(ρ) = 0.
Исследуем константу разделения μ . Решаем уравнение (6.4.4).
Выписываем характеристический полином: p2 - μ = 0 . Полином имеет два
корня: p1 =		и p2 = -				. Решение уравнения (6.4.4) примет следующий вид:
	μ				μ
		F(ϕ) = A× e					μ	ϕ + B ×e−	μ	ϕ .	(6.4.6)
Пусть μ > 0. Анализируя (6.4.6),									видим, что функция F(ϕ)		не является

периодической. Исключаем				μ > 0 из дальнейшего рассмотрения. Пусть μ = 0.
Тогда уравнение	(6.4.4)			′′
			имеет вид Φ (ϕ) = 0 , интегрируя которое, получим
F(ϕ) = C ×ϕ + D ,	где	C ,	D	– константы. Исключаем	μ = 0	из дальнейшего
рассмотрения. Пусть		μ < 0.		Полагаем μ = -λ2, λ Î R .	Тогда	решение (6.4.4)
представимо в виде
	F(ϕ) = A×cosλϕ + B ×sin λϕ .					(6.4.7)

Данное решение согласуется с физическим смыслом задачи (6.4.1). II этап. Формируем задачу Штурма – Лиувилля, полагая μ =-λ 2, λÎR :

ρ 2 ×R ¢¢( ρ ) + ρ ×R ¢( ρ ) - λ2 ×R ( ρ ) = 0,	(6.4.8)
R(1)= g (ϕ)/Φ(ϕ).	(6.4.9)
Решаем дифференциальное уравнение (6.4.8),	которое называется

100

уравнением Эйлера. Оно является линейным обыкновенным однородным

дифференциальным			уравнением второго порядка с				непостоянными
коэффициентами.	Сделаем подстановку			R(ρ) = ρ	n		¢	n−1	,
						. Поскольку R (ρ)=n×ρ
¢¢	n−2	,	′		′′
R (ρ) = n ×(n -1) × ρ			то, вписывая R (ρ) и R (ρ) в уравнение (6.4.8),
получаем ρ2 × n ×(n -1) × ρn−2 + ρ × n × ρn−1 - λ 2× ρn = 0 , или, что то же самое:
			n 2- λ 2= 0.				(6.4.10)
Находим корни уравнения (6.4.10):				n = ± λ	( λ = ± n).		Поскольку корни

действительные и кратность каждого корня равна единице, общее решение уравнения (6.4.8) будет иметь следующий вид:

R n (ρ) = C × ρn + D × ρ −n .	(6.4.11)
Для определенности можно ограничиться	только положительными

значениями n , так как в силу произвола выбора констант C, D отрицательные

значения n новых частных решений не дают. Поскольку ищется решение конечное в круге G = {0 ≤ ρ ≤ 1, ϕ[ 0 ,2р ] }, в формуле (6.4.11) положим D = 0 ,

т.е. R n (ρ) = C× ρ n .

Подставляя (6.4.7) и (6.4.11) в представление (6.4.2), окончательно

получаем		(ρ,ϕ) = F		(ϕ) × R (ρ) = (A× cos(nϕ) + B ×sin(nϕ)) × ρ n .
u	n		n		(6.4.12)
				n
Функция (6.4.12) будет элементарным решением уравнения (6.4.1).
III Этап. Решение краевой задачи (6.4.1) будем искать в виде следующего
ряда:				∞
		u(ρ, ϕ) = A 0 + å(An cosnϕ + Bn sin nϕ)ρ n .			(6.4.13)
				n=1

Подберём произвольные постоянные An и Bn так, чтобы удовлетворялось

краевое условие задачи (6.4.1). Подставляя в равенство (6.4.13)									ρ =1, получаем
				g(ϕ) = A 0 +		∞			(6.4.14)
						å (An cos nϕ + Bn sin nϕ) .
						n=1
Потребуем, чтобы ряд (6.4.14)						являлся рядом Фурье функции g(ϕ) на
интервале (0, 2π ) с коэффициентами						An , Bn :
1		2π				1		2π
A0 =		ò0		g(ϕ) dϕ, An =				ò0g(ϕ)cos(nϕ)dϕ,n=1,2,....
	2π						π
			1		2π
	Bn =				òg(ϕ)sin(nϕ)dϕ,n=1,2,... .				(6.4.15)
			π
				0

Окончательно получаем, что ортогональный ряд (6.4.13) с коэффициентами, определёнными (6.4.15), доставляет формальное решение краевой задаче (6.4.1).

Теорема. Если функция g (ϕ) на окружности ∂G = { ρ = 1, ϕ [ 0 ,2р ] }

дважды непрерывно дифференцируема, имеет кусочно-непрерывную третью производную, то существует единственное решение u(ρ,ϕ) граничной задачи

101

Дирихле (6.4.1). Функция u(ρ,ϕ) , определяемая абсолютно и равномерно сходящимся рядом (6.4.13), в котором коэффициенты An и B n вычисляются по

формулам (6.4.15), имеет непрерывные вторые производные по совокупности переменных ρ , ϕ . Причем возможно почленное дифференцирование ряда (6.4.13) по ρ и по ϕ дважды. При этом полученные ряды сходятся абсолютно и равномерно на G = { ρ [0 ,1] , ϕ[ 0 ,2р ] }.

Задачи для решения. Решить эллиптическую краевую задачу Дирихле ρ [0 ,1], ϕ[0 , 2π ] с проверкой решения:

u=0, 1. u(1,ϕ)=2.

u=0,

4. u(1,ϕ)=1+sinϕ.

		u =0,				u =0,
	2.	u(1,ϕ)=sinϕ.				3. u(1,ϕ)=cosϕ.
		u =0,				u =0,
	5. u(1,ϕ)=sinϕ +		1		6.
				cosϕ.		u(1,ϕ)=1+sinϕ +sin2ϕ.
			2

Приведем скрипт в ToolBox PDE среды MATLAB решения задачи Дирихле, заданной на треугольной области G : x > 0, y > 0, x + y < 1 и

удовлетворяющую на границе области ∂G : x = 0, y = 0, x + y = 1 условию

u |∂G = x2 + y2 (отдельно отметим, что в §8 эта же задача будет решена методом Ритца).

1.%решение эллиптической задачи Дирихле для треугольной области

2.clear all;

3.format long;

4.syms x y z D2zx2 D2zxy D2zy2; % переменные

5.LapL=D2zx2+D2zy2; % левая часть уравнения Лапласа

6.LapR=0; % правая часть уравнения Лапласа

7.zc=x^2+y^2; % граничное условие

8.[p,e,t]=initmesh('triangleg','hmax',0.025); % формируем FEM-сетку

9.np=size(p,2); % число узлов

10.nel=size(t,2); % число элементов

11.fprintf('Число узлов сетки разбиения np=%d\n',np);

12.fprintf('Число конечных элементов nel=%d\n',nel);

13.da=daspect; % текущие масштабы осей

14.da(1:2)=min(da(1:2)); % выравняли масштабы

15.daspect(da);

16.% --------------задание граничных условий--------------------------------

17.s{1}='function [q,g,h,r]=boundmem(p,e,u,time)'; % заголовок

18.s{2}='nb=size(e,2);'; % определили размерности

19.s{3}='q=zeros(1,nb); g=zeros(1,nb);'; % задали массивы условий Неймана

20.s{4}='h=ones(1,2*nb); r=zeros(1,2*nb);'; % задали массивы условий Дирихле

21.s{5}='xb=[p(1,e(1,:)),p(1,e(2,:))];'; % столбец координат x

22.s{6}='yb=[p(2,e(1,:)),p(2,e(2,:))];'; % столбец координат y

23.zcf=subs(zc,{x,y},{sym('xb'),sym('yb')}); % формула для подстановки

24.s{7}=['r=' vectorize(zcf) ';'];

25.disp('Текст файла граничных условий boundmem.m:')

26.fprintf('%s\n',s{:})

27.fid = fopen ('C:\MATLAB701\work\boundmem.m', 'w' );

102

28.fprintf(fid,'%s\n',s{:});

29.fclose(fid); % закрываем файл

30.% --------задание функций, входящих в дифференциальное уравнение--------

31.a=eval(subs(LapL,{z,D2zx2,D2zxy,D2zy2},{1,0,0,0}));

32.c11=-eval(subs(LapL,{z,D2zx2,D2zxy,D2zy2},{0,1,0,0}));

33.c12=-eval(subs(LapL,{z,D2zx2,D2zxy,D2zy2},{0,0,1,0}));

34.c22=-eval(subs(LapL,{z,D2zx2,D2zxy,D2zy2},{0,0,0,1}));

35.c=[c11;c12;c12;c22];

36.fp = subs(LapR,{x,y},{p(1,:),p(2,:)}); % f в узлах

37.if (length(fp)>1)

38.f = (fp(t(1,:))+fp(t(2,:))+fp(t(3,:)))/3; % f в ц.т. конечных элементов

39.else

40.f = 0; end;

41.%-------------------Визуализируем решение-------------------------------

42.u = assempde('boundmem',p,e,t,c,a,f); % решили

43.pdeplot(p,e,t,'xydata',u,'zdata',u,'mesh','on','colorbar','off'); % рисуем

44.title ('\bfFEM method') % заголовок

45.xlabel('x'); ylabel('y'); zlabel('z(x,y)');

46.v = axis; % границы осей

47.da = daspect; % масштаб осей

48.da(1:2) = min(da(1:2)); % min из двух

49.daspect(da) % выравняли масштаб осей

50.axis(v); % оставили границы

51.colormap(gray) % выбрали палитру

52.grid on % показали сетку

53.box on % показали внешний контур

1.% функция описания геометрии области, на которой строится решение

2.function [x,y]=triangleg(bs,s)

3.% Описывает геометрические данные для треугольной области

4.% NE=TRIANGLEG возвращает количество граничных участков

5.% D=TRIANGLEG(BS) возвращает матрицу с одной колонкой для каждого

6.% граничного участка, определенного в BS

7.% [X,Y]=TRIANGLEG(BS,S) возвращает координаты граничных точек

8.% BS определяет граничные участки и S соответствующие

9.% значения параметра BS может быть скаляром

10.nbs=3;

11.if nargin==0,

12.x=nbs; % количество граничных участков

13.return

14.end;

15.d=[

16.0 0 0 % начальное значение параметра

17.1 1 1 % конечное значение параметра

18.0 0 0 % номер левосторонней области

19.1 1 1 % номер правосторонней области

20.];

21.bs1=bs(:)';

22.if nargin==1,

23.x=d(:,bs1);

24.return

25.end;

26.x=zeros(size(s));

103

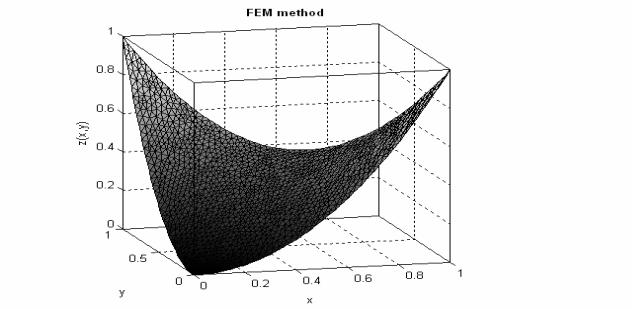
27.y=zeros(size(s));

28.[m,n]=size(bs);

29.if m==1 && n==1,

30.bs=bs*ones(size(s)); end;

31.if ~isempty(s),

32.ii=find(bs==1); % граничный участок 1

33.if length(ii)

34.x(ii)=interp1([d(1,1),d(2,1)],[0 1],s(ii));

35.y(ii)=interp1([d(1,1),d(2,1)],[1 0],s(ii)); end;

36.ii=find(bs==2); % граничный участок 2

37.if length(ii)

38.x(ii)=interp1([d(1,2),d(2,2)],[1 0],s(ii));

39.y(ii)=interp1([d(1,2),d(2,2)],[0 0],s(ii)); end;

40.ii=find(bs==3); % граничный участок 3

41.if length(ii)

42.x(ii)=interp1([d(1,3),d(2,3)],[0 0],s(ii));

43.y(ii)=interp1([d(1,3),d(2,3)],[0 1],s(ii));

44.end; end;

Ниже приведена визуализация полученного решения:

§5. Анализ решения задачи Дирихле. Интегральная формула Пуассона

Если граничное условие g(ϕ) уже представимо конечным числом

слагаемых своего разложения в тригонометрический ряд Фурье, то решение задачи Дирихле выписывается почти автоматически. Пусть дана задача:

u = 0,

u (1,ϕ ) =1+ sin ϕ + 12 sin 3ϕ + cos 4ϕ .

Тогда решение данной задачи будет иметь следующий вид:

	u(ρ,ϕ) =1+ ρ ×sinϕ +	1	ρ3 ×sin 3ϕ + ρ 4	×cos4ϕ , поскольку в данном случае
		2
	104

граничные условия g (ϕ )

уже разложены в тригонометрический ряд Фурье со

следующими коэффициентами:

a0 =1,

a1

= 0,

a2

= 0, a3

= 0,

a4

=1,

2π

a5 = 0,

1

1

g(ϕ)dϕ

b1 =1, b2 =0,

b3 =

, b4 =0, ... .

Отметим,

что

коэффициент a0

=

ò0

2

2π

является средним значением функции g (ϕ ) .

Выпишем решение задачи Дирихле, заданной на круге произвольным

радиусом R :

ρ ön

∞

æ

u(ρ,ϕ) = å

ç

÷ (an cos(nϕ) + bn sin(nϕ)) .

n=0

è

R ø

Подставим формулы (6.4.15) для подсчета коэффициентов an и bn.

Получаем следующее представление:

1

2π

1

∞ æ ρ

ön 2π

u(ρ,ϕ) =

ò g(ϕ)dϕ +

åç

÷

× òg(ϕ)(cos(nα) ×cos(nϕ) + sin(nα) ×sin(nϕ))dα =

2π

0

π n=1è R

ø

0

1 2π

ì

∞

æ ρ

ön

ü

=

í1 + 2 å

ç

÷

(cos (ϕ - α ) )ýg(α )dα .

2π ò0 î

n=1

è R

ø

þ

Преобразуем выражение, стоящее в фигурных скобках:

]=

∞ æ

ρ ön

∞ æ

ρ ön

in(ϕ−α)

+ e

−in(ϕ−α)

1+ 2åç

÷ cosn(ϕ -α) =1+ åç

÷

[e

n=1è

R ø

n=1è

R ø

∞ éæ =1+ åêç n=1ëè

=

ρ

n

ρ

n

ρ

ei(ϕ −α )

ρ

e−i (ϕ−α )

e

÷ + ç

e

÷

ú =1+

R

+ R

=

i(ϕ −α ) ö

æ

−i(ϕ −α ) ö

ù

R

ø

è

R

ø û

ρ

i(ϕ −α )

ρ

−i(ϕ −α )

1

-

e

1-

e

ρ ö2

R

R

æ

1 - ç

÷

R 2 - ρ 2

è

R ø

=

.

1 - 2

ρ

cos( ϕ - α )

æ

ρ ö2

R 2 - 2 ρ R cos( ϕ - α ) + ρ 2

+ ç

÷

R

è

R ø

Окончательно получаем

2р

é

2

R

- ρ

ù

u(ρ , ϕ ) = 1 ò g(α ) ê

2

2

2 ú dα .

0

ë

2π

R

- 2 ρ R cos(ϕ - α ) + ρ

û

Данное выражение называется интегральной формулой Пуассона.

Получено еще одно представление решения внутренней задачи Дирихле.

Замечание: Отметим,

что

выражение

R 2 − ρ 2

часто

R 2 − 2 ρ R cos (ϕ − α )+ ρ 2

называют ядром Пуассона.

105

ИСТОРИЧЕСКАЯ СПРАВКА

Пуассон Симеон Дени (1781 – 1840) – выдающийся французский математик, физик, механик. Член Парижской Академии наук. С 1816 г. – профессор в Сорбонне. В двухтомном курсе механики Пуассон развил идеи Ж. Лагранжа и П. Лапласа. Пуассон

основательно разработал многие разделы математической физики, дал решения многих задач электростатики и магнитостатики. Предложил общие

методы интегрирования дифференциальных уравнений теории упругости. Существенное значение имеют работы Пуассона, посвященные уравнениям в конечных разностях, дифференциальным уравнениям с частными производными, вариационному исчислению, ортогональным рядам.

§6. Задача оптимального управления эллиптической системой

Приведем результат поиска оптимального управления в задаче управления дифференциальным уравнением эллиптического типа. Задачи

такого типа часто встречаются в практических приложениях управления установившимися процессами.

Пусть дано дифференциальное уравнение

	∂2 z	+	∂2 z	+	∂2 z	= F(x, z, u) ,	(6.6.1)
	∂x2		∂x2		∂x2
1			2		3
где нелинейная функция					F непрерывна по		x = (x1, x2 , x3 ) в области D

трёхмерного евклидова пространства и дважды непрерывно дифференцируема по совокупности переменных z и u , где u – некоторый r -мерный параметр, принимающий всевозможные значения из некоторой ограниченной области U

(открытой или замкнутой) r -мерного евклидова пространства.
Пусть S достаточно гладкая граница области D . Потребуем,			чтобы
искомая функция z(x, y) удовлетворяла условию
	dz	+ hz = f (x) при x S ,	(6.6.2)
	dn

где n – направление внешней нормали, h – положительная постоянная, а f (x)

– ограниченная кусочно-непрерывная на S функция.

Функцию u = u(x) , определённую в области D , будем называть

допустимой, если её значения расположены в U и она может иметь лишь конечное число поверхностей, линий и точек разрыва. Потребуем, чтобы в

окрестности любой точки поверхности разрыва можно было ввести невырожденное преобразование координат ξi = ξi (x), i = 1, 2, 3 , такое, что эта

поверхность переходит в кусок плоскости ξ3 = 0 . Вставляя такую допустимую

106

	функцию в уравнение (6.6.1), получим			∂2 z		∂2 z		∂2 z
	z = F(x, z, u(x)),		≡		+		+		.	(6.6.3)
				∂x2		∂x2		∂x2
				1		2		3
	Это уравнение уже не содержит параметра. Согласно условиям,
	наложенным на F и u(x) ,	его правая часть является кусочно-непрерывной
	функцией. Поверхности	i , i=1,K,k ,	разрыва управления u(x)							разбивают
	область D на конечное число подобластей,				в каждой из которых правая часть

уравнения (3) непрерывна. Под решением краевой задачи (6.6.3), (6.6.2) будем понимать функцию z = z(x) , которая удовлетворяет уравнению (6.6.3), условию

(6.6.2) и некоторым дополнительным условиям гладкости на i . Будем

предполагать, что заданные функции в уравнениях (6.6.1) и условиях (6.6.2), кроме перечисленных выше свойств, удовлетворяют ещё условиям, при которых каждой допустимой функции u = u(x) соответствует единственное

решение рассматриваемой краевой задачи (6.6.3), (6.6.2). Это решение будем называть решением, соответствующим допустимой функции u = u(x) .

Пусть задан функционал

I = òòα (x)z(x)dS + òòòβ (x)z(x)dx ,

S D

где α (x) и β (x) – интегрируемые со своим квадратом функции, определённые

соответственно в областях S и D .

Ставится задача: среди всех допустимых функций найти такую, что соответствующее ей решение уравнения (6.6.1), удовлетворяющее условию (6.6.2), реализует минимум (максимум) функционала I .

Функцию u(x) , для которой функционал I достигает своего минимума

(максимума), будем называть минимизирующей (максимизирующей) функцией.

Пусть u(x) – некоторая допустимая функция, а z(x) – соответствующее

ей решение уравнения (6.6.3) с граничным условием (6.6.2). Введём функцию ω (x), определив её как решение сопряженного уравнения

ω = ∂F(x, z(x), u(x))ω − β (x)

∂z

с граничным условием

ddnω + hω = α(x) при x S ,

где α (x) и β (x) – функции, входящие в определение функционала I .

(6.6.4)

(6.6.5)

Данными соотношениями функция ω (x) определяется однозначно и

оказывается интегрируемой с квадратом по области D . Таким образом, каждая допустимая функция u(x) однозначно определяет пару функций z(x) и ω(x).

Введём обозначение (гамильтониан системы)

H (ω(x), z(x), u, x) = ω(x)F(x, z(x), u) .

107

(6.7.1) y Ξ ,

Будем говорить, что допустимая функция	u = u(x)	удовлетворяет
условию максимума, если
H (ω (x), z(x), u(x), x)(=) Sup H (ω (x), z(x), u, x) ,		(6.6.6)
u U
где z(x) и ω(x) – решения краевых задач (6.6.3),	(6.6.2) и	(6.6.4), (6.6.5),
соответствующие допустимой функции u = u(x) .	Символ	(=) означает

равенство, справедливое во всех точках области D , за исключением, быть может, множеств точек нулевой меры. Условие минимума определяется аналогично.

Сформулируем следующую теорему.

Принцип максимума (А. И. Егорова) Для того чтобы допустимая функция была минимизирующей (максимизирующей), необходимо, чтобы она удовлетворяла условию максимума (минимума).

Хотя принцип максимума формально не даёт достаточных условий существования минимизирующих (максимизирующих) функций, он служит практическим инструментом для их отыскания, поскольку уравнения (6.6.1), (6.6.4), (6.6.6) вместе с граничными условиями (6.6.2), (6.6.5) образуют полную

систему отношений для определения искомых функций и соответствующих им решений краевой задачи (6.6.1), (6.6.2).

Таким образом, рассмотренная вариационная задача сводится к решению

эллиптических дифференциальных уравнений в частных производных с соответствующими граничными условиями.

§7. Основы вариационного метода решения краевых задач

Пусть в области G с границей ∂G дано линейное дифференциальное уравнение – обыкновенное или в частных производных. Требуется найти решение y этого уравнения, удовлетворяющее на границе ∂G заданным

линейным однородным (краевым) условиям. Левую часть уравнения можно рассматривать как линейный оператор L , определённый на множестве Ξ функций, обладающий непрерывными производными нужного порядка в G + ∂G и удовлетворяющий данным краевым условиям на ∂G . Таким образом,

наша краевая задача сводится к решению операторного уравнения

Ly = f (P),

f (P) – известная функция (которую мы будем считать непрерывной) и

причём функция y на границе ∂G удовлетворяет краевому условию
	R[y] = 0 ,		(6.7.2)
где	R – известный линейный оператор более низкого порядка. Заметим, что
неоднородная краевая задача
	Ly = f (P),		(6.7.3)
	R[y] = ϕ (P) ,	P ∂G ,	(6.7.4)
где	ϕ ( P ) – известная функция,	сводится к однородной, если	положить

y = z + y1 , где z – новая неизвестная функция и y1 , удовлетворяющая краевому

108

условию (4): R[ y1]=ϕ (P) . Действительно, из формул (6.7.3) и (6.7.4) получаем Lz = f (P) − Ly1 и R[z]=0. Функцию y1 обычно нетрудно найти подбором.

Идея вариационного подхода состоит в том, что краевая задача (6.7.1), (6.7.2) заменяется эквивалентной задачей об отыскании функции, доставляющей экстремум (обычно минимум) некоторому функционалу.

Вариационные методы решения краевых задач неразрывно связаны с именами Б. Г. Галеркина, В. Ритца, И. Г. Бубнова, которые предложили численные процедуры приближённого решения соответствующих задач. Приведём две важные для дальнейшего теоремы.

Теорема 1. Пусть L – самосопряженный линейный оператор, положительно-определенный в классе функций Ξ . Тогда операторное уравнение (6.7.1) при наличии краевого условия (6.7.2) в классе Ξ не может иметь двух решений. Если решение краевой задачи (6.7.1) – (6.7.2) существует, то оно единственно.

Доказательство. Предположим, что краевая задача (6.7.1) – (6.7.2) имеет два решения y1 и y2 ,

Ly1 = f (P) , R[y1] = 0 ,	(6.7.5)
Ly2 = f (P) , R[y2 ] = 0.	(6.7.6)

Вычитая из уравнений (6.7.5) соответствующие уравнения (6.7.6), в силу

линейности	оператора L и	функционала	R	получим	L( y1 − y2 ) = 0 ,
R[y1 − y2 ] = 0 , т.е. ( y1 − y2 ) Ξ .		Умножая первое		из полученных		равенств
скалярно на разность (y1 − y2 ) , будем иметь
	(L( y1 − y2 ),(y1 − y2 )) = 0.					(6.7.7)
Так как по	условию оператор L положительный в классе				Ξ и	функция
( y1 − y2 ) Ξ ,	то из формулы (6.7.7) следует		(y1 − y2 ) ≡ 0 , т.е.		y1 ≡ y2 , что и
требовалось доказать.
Теорема 2. Пусть L – самосопряженный оператор, положительно-
определенный в классе Ξ , а F[ y] – функционал вида
	F [ y] = (Ly, y) − 2( f , y) ≡ ò(Ly − 2 f ) y dω ,					(6.7.8)
		ω
где f = f (P)	– правая часть уравнения (6.7.1).

Если краевая задача (6.7.1) – (6.7.2) с однородными граничными условиями имеет решение y , то это решение даёт минимум функционалу F[ y] .

Если в классе Ξ существует функция y , дающая минимум функционалу

(6.7.9), то эта функция является решением уравнения (6.7.1).
Доказательство. Пусть y	есть решение краевой задачи (6.7.1) – (6.7.2),
т.е. Ly = f (P) и R[y] = 0. Заменяя	f (P) через Ly в формуле (6.7.8), получим
F [ y] = (Ly, y) − 2(Ly, y) .		(6.7.9)
Пользуясь симметричностью оператора L , получаем:
(Ly, y) = ( y, Ly) = (Ly, y) .
		109

Поэтому

F[y] = (Ly, y) - (Ly, y) - (Ly, y) = (Ly, y - y) -[(Ly, y) - (Ly, y)] - (Ly, y) =

= (Ly, y - y) - (Ly, y - y) - (Ly, y) = (L( y - y),(y - y)) - (Ly, y) . (6.7.10)

В правой части формулы (6.7.10) только первое слагаемое является переменным. Очевидно, (y - y)ÎX , поэтому в силу положительности

оператора L получаем (L( y - y),(y - y)) ³ 0. Следовательно, функционал F[ y]

достигает своего наименьшего значение для тех и только тех допустимых функций y , для которых имеет месть равенство (L( y - y),(y - y)) = 0 . Отсюда

на основании определения положительного оператора получаем y - y º 0, т.е. y ≡ y .

Заметим, что из формулы (6.7.10) следует, что наименьшее значение

функционала F[ y] равно Fmin (y) = F[ y] = -(Ly, y) .
Пусть	существует функция y	из класса X ,	дающая	минимум
функционалу (6.7.8). Это значит, что для любой функции			y1 X и достаточно
близкой к y	справедливо следующее неравенство:
	F[y1] - F[y] ³ 0.
Положим η = ( y1 - y)ÎX и рассмотрим семейство функций
	y = y + αη ,			(6.7.11)
где α – числовой параметр. Очевидно,		при любом α функции y		являются
допустимыми и при достаточно малом | α | выполнено неравенство
	DF = F[y] - F[y] ³ 0 .

На основании формулы (6.7.8), выполняя тождественные преобразования,

получаем

DF = (Ly, y) - 2( f , y) - (Ly, y) + 2( f , y) =
= (Ly, y) - 2(Ly, y) + 2(Ly - f , y) - 2(Ly - f , y) + (Ly, y) =
= (Ly, y) - 2(Ly, y) + 2(Ly - f , y - y) + (Ly, y) ³ 0 .	(6.7.12)

Отсюда, используя преобразование (6.7.10) и формулу (6.7.11), находим

DF = ((L( y - y),(y - y)) - (Ly, y) + 2(Ly - f , y - y) = α 2 (Lη,η) + 2α(Ly - f ,η) ³ 0 .

Левая часть данного неравенства представляет собой квадратный трехчлен относительно параметра α , причём этот трёхчлен не может менять знака. Следовательно, соответствующее квадратное уравнение заведомо не имеет действительных различных корней и, значит, обладает неположительным дискриминантом: (Ly - f ,η)2 - (Lη,η) × 0 £ 0. Отсюда (Ly - f ,η)2 = 0. Таким

образом, ωò(Ly − f )η dω = 0 для любой функции η ÎX . В силу произвола выбора

функции η отсюда следует, что Ly - f º 0 , т.е. Ly º f . Таким образом, y есть решение нашей краевой задачи.

110

ИСТОРИЧЕСКАЯ СПРАВКА

Бубнов Иван Григорьевич (1872 – 1919) – выдающийся русский инженер и математик. Основоположник строительной механики корабля, создатель первых боевых подводных лодок России. Окончил Морское инженерное училище в Кронштадте (1891), Морскую академию (1896).

Профессор Политехнического института и Николаевской морской академии. В своих работах И. Г. Бубнов

математически исследовал вопросы упругости и прочности судов. Разработал метод нахождения приближенного решения операторного уравнения, который применил к решению ряда задач теории упругости. Этот метод был усовершенствован Б. Г. Галеркиным и сейчас называется методом Бубнова – Галеркина.

Рассмотрим приведенный выше подход применительно к краевым задачам для уравнений Пуассона и Лапласа. Пусть дано уравнение Пуассона

			− u = f (x, y), f (x, y) C(G) .			(6.7.13)
		Требуется найти решение уравнения, непрерывное в замкнутой области
		= G È ¶G	и удовлетворяющее на границе ∂G этой области			краевому
	G
условию					∂G = ϕ (P),
			u			(6.7.14)
где P = (x, y)			и ϕ(P) – заданная непрерывная функция. Предположим вначале,
что ϕ (P) ≡ 0 , т.е.
			u		∂G = 0,	(6.7.15)

и будем решать однородную краевую задачу (6.7.13), (6.7.15). Покажем, что в классе функций Ξ = {u(x)}, непрерывных в G вместе со своими первыми и

вторыми производными и обращающихся на контуре ∂G в нуль, оператор Lu = − u самосопряжен и положителен.

Пусть u Ξ и v Ξ . Составим выражение

é

æ

¶2u ¶2u ö

æ

¶2v ¶2v öù

(Lu,v) - (Lv,u) = òò

ç

2

+

2

÷

ç

2 +

÷

ê- vç

¶x

¶y

÷

+ uç

¶x

¶y

2 ÷údxdy =

G

ë

è

ø

è

øû

é

¶2v

¶

æ

¶v

ö

¶u ¶v

¶2u

¶

æ

¶u

ö

¶v ¶u

=

êu

2

=

çu

÷

-

, - v

2

= -

çv

÷ +

,

¶x

¶x

¶x

¶x

¶x

¶x

¶x

¶x ¶x

ë

è

ø

¶x è

ø

¶2v

¶

æ

¶v ö

¶u ¶v

¶2u

¶

æ

¶u ö

¶v ¶u ù

u

2

=

çu

÷ -

, - v

2

= -

çv

÷ +

ú

=

¶y

¶y

ç

÷

¶y ¶y

¶y

ç

¶y

÷

è

¶y ø

¶y è

ø

¶y ¶y û

é

¶

æ

¶v

¶u ö

¶

æ

¶v

¶u

öù

òòê

ç

÷ú

=

çu

- v

÷ -

ç- u

+ v

÷ dxdy .

G ë

¶x

è

¶x

¶x

ø

¶y è

¶y

¶y

øû

111

Используя формулу Грина	ò	Pdx + Qdy =	æ	¶Q	-	¶P ö	и используя
			ç			÷
			òò ç	¶x		÷
	∂G		G è			¶y ø

нулевые граничные условия

u

∂G = 0,

v

∂G = 0,

получим, что

(Lu,v) - (Lv,u) =

ò

é

æ

¶v

- v

¶u

ö

æ

¶v

- v

¶u ö

ù

= 0.

(6.7.16)

ê

- çu

÷dx

+ çu

÷dy

ú

ç

¶y

¶y

÷

è ¶x

¶x ø

∂G

ë

è

ø

û

Следовательно, (Lu,v) = (Lv,u) . Поэтому оператор L самосопряжен.

Далее установим, что оператор L является положительно-определенным.

Получаем

æ

¶

2

u

¶

2

u

ö

(Lu,u) = -òòu

ç

+

÷

=

ç

¶x

2

¶y

2

dxdy

G

÷

è

ø

é

¶2u

¶ æ

¶u ö æ

¶u

ö2

¶2u

¶

æ

¶u ö æ

¶u ö2 ù

= ê- u

¶x2

= -

çu

÷

+ ç ÷

, - u

¶y2

= -

çu

÷

+ ç ÷

ú =

ê

¶x è

¶x ø è

¶x

ø

¶y ç

¶y ÷ ç

¶y ÷

ú

è

ø

è

ø

ë

û

é

¶ æ

¶u

ö

¶

æ

¶u

öù

éæ ¶u ö2

æ

¶u

ö2 ù

= -

òòê

çu

÷ +

ç

÷ú

òò

êç

÷

+

ç

÷

G ë

¶x

¶y

çu

¶y

÷

dxdy +

ç

¶y

÷ údxdy .

¶x è

ø

è

øû

G êè

¶x ø

è

ø ú

ë

û

Применяя к первому интегралу формулу Грина, в силу краевых условий

для функции u получим

éæ ¶u ö2

ö2 ù

(Lu,u) = -

ò

æ

- u

¶u

dx + u

¶u

dy

ö

+

òò

+

æ

¶u

ç

÷

êç

÷

ç

÷

ç

¶y

¶x

÷

ç

¶y

÷ údxdy =

∂G è

ø

êè ¶x ø

è

ø ú

ö2 ù

G ë

û

òò

éæ ¶u ö2

æ

¶u

(6.7.17)

=

êç

ç

÷

ú dxdy,

÷ + ç

¶y

÷

G

êè ¶x ø

è

ø ú

ë

û

т.е. (Lu,u) = (-Du,u) ³ 0 . Если (Lu,u) = 0,

то из формулы (6.7.17)

следует, что

∂u

=

∂u

= 0.

Отсюда

u(x, y) = c ,

и

на

основании

краевого

условия

(6.7.15)

¶x

¶y

u(x, y) º 0 .

L

следует

Следовательно,

оператор

является

положительно-

определенным оператором. Таким образом, для краевой задачи (6.7.13) с однородными краевыми условиями (6.7.15) выполнены условия теоремы 2. Следовательно, эта задача эквивалентна вариационной задаче для функционала

F[u] = (Lu,u) - 2(u, f )							(6.7.18)
в классе X функций. В силу формулы (6.7.17) получаем
F[u] =	òò	éæ ¶u ö2		æ	¶u ö2	ù	(6.7.19)
		êç	÷	ç	÷
				+ ç	÷ - 2 fuúdxdy .
	G	êè	¶x ø	è	¶y ø	ú
		ë				û
Рассмотрим теперь уравнение (6.7.13) с неоднородным краевым условием
(6.7.14), и пусть Ξ = {u(x, y)}				–	класс	функций	u C(2) (G + ∂G) ,

1

удовлетворяющих условиям (6.7.14).

112

Следуя

идее

предыдущего

параграфа,

построим

функцию

z = z(x, y) C(2) (G + ∂G) , для которой выполнены краевые условия (6.7.14).

Введём функцию

v(x, y) = u(x, y) − z(x, y) ,

(6.7.20)

где u(x, y) –

решение нашей неоднородной краевой задачи. Тогда функция

ν =ν (x, y) удовлетворяет на контуре ∂G однородному краевому условию

v

∂G = 0

(6.7.21)

и является решением уравнения

Lv = Lu − Lz = f (P) − Lz ,

(6.7.22)

æ

¶

2

z

+ ¶

2

z

ö

– известная функция. Функция v = v(x, y) , являясь

где Lz = -ç

÷

ç

¶x

2

¶y

2

÷

è

ø

решением однородной краевой задачи (6.7.21) – (6.7.22), на основании формулы (6.7.18) даёт наименьшее значение функционалу

F[v] = (Lv,v) − 2(v, f (P) − Lz) .

(6.7.23)

Возвращаясь в последнем равенстве к функции u (см. (6.7.20)) и используя свойства скалярного произведения и линейного оператора L , получим

F[u − z] ≡ F1[u] = (L(u − z),u − z) − 2(u − z, f (P) − Lz) =

= (Lu,u) − 2(u, f ) + (u, Lz) − (z, Lu) + 2(z, f ) − (Lz, z) .

(6.7.24)

Так как последние два члена формулы (6.7.24) не зависят от искомой функции u = u(x, y), то функция u = u (x, y) , дающая наименьшее значение функционалу

(6.7.24), будет минимизировать функционал

F2[u]= (Lu ,u)- 2(u, f )+[( Lz ,u)-(Lu ,z)] .

(6.7.25)

Покажем, что функционал (6.7.25) можно заменить функционалом, не содержащим функцию z . Используя преобразование, применённое в формуле

(6.7.16), имеем

				é	æ	¶u		¶z	ö
	(Lz ,u) -(Lu ,z) =	òò	(zDu -uDz)dz =	ò ê	-ç z		-u		÷dx
					ç	¶y			÷
		G		∂G ë	è			¶y ø

æ	¶u		¶z ö
= ò ç z	¶n	- u		÷dS ,
∂G è			¶n ø

æ	¶u		¶z ö		ù
+ç z	¶x	-u		÷dy ú		=
è			¶x ø		û

где n – внешняя нормаль к ∂G и

∂u

=

∂u

∂y

-

∂u

∂x

,

∂z

=

∂z

∂y

-

∂z

∂x

.

¶n

¶x ¶S

¶y ¶S

¶n

¶x ¶S

¶y ¶S

Отсюда, так как z

∂G = u

∂G = ϕ(x, y) , получаем

æ ¶u

¶z

ö

(Lz,u) - (Lz,u) =

ò ϕ(x, y)ç

¶n

-

÷dS .

(6.7.26)

∂G

è

¶n ø

С другой стороны, на основании формулы (6.7.17) находим

ò

æ

¶u

ö

òò

éæ

¶u ö2

æ

¶u ö2 ù

(Lu,u) = -

çu

dS ÷ +

êç

÷

ç

÷

ú dxdy =

¶n

+ ç

÷

∂G è

ø

G êè

¶x ø

è

¶y ø ú

ë

û

113

ò

æ

¶u

ö

òò

éæ ¶u ö2

æ

¶u ö2 ù

= -

çϕ(x, y)

dS ÷ +

êç

÷

ç

÷

(6.7.27)

¶n

+ ç

÷ ú dxdy .

∂G

è

ø

G êè

¶x ø

è

¶y ø ú

ë

û

Подставляя (6.7.26) и (6.7.27) в формулу (6.7.25), будем иметь

2

òò

éæ ¶u ö2

æ

¶u ö2

ù

ò

æ

¶z

ö

êç

÷

ç

÷

- 2 fuúdxdy -

çϕ(x, y)

dS ÷ .

(6.7.28)

F [u] =

+ ç

÷

¶n

G

êè

¶x ø

è

¶y ø

ú

∂G è

ø

ë

û

Так как

последнее

слагаемое

в

формуле

(6.7.28)

не

зависит от

функции u , то краевая задача (6.7.13) – (6.7.14) эквивалентна вариационной

задаче для функционала

	òò	éæ ¶u ö2		æ	¶u ö2	ù	(6.7.29)
F[u]=		êç	÷	ç	÷	- 2 fuú dx dy
				+ ç	÷
	G	êè	¶x ø	è	¶y ø	ú
в классе функций Ξ1 .		ë				û
		f = f (x, y) ≡ 0,
В частном случае, если						то получаем уравнение Лапласа

u = 0, причём краевая задача (6.7.13) – (6.7.14) есть известная задача Дирихле. Решением этой задачи, как вытекает из формулы (6.7.29), является функция u

из		класса			Ξ1 ,		минимизирующая	интеграл	Дирихле
	òò	éæ ¶u ö2		æ	¶u ö2 ù
F[u] =		êç	÷	ç	÷	údxdy .	Убедиться в этом	самостоятельно,	выписав
				+ ç	÷
	G	êè	¶x ø	è	¶y ø	ú
		ë				û

уравнение Остроградского для данного функционала.

ИСТОРИЧЕСКАЯ СПРАВКА

Галёркин Борис Григорьевич (1871 – 1945) – выдающийся русский советский математик и инженер. Специалист в области теории упругости. Родился в Полоцке. В 1899 г. окончил Петербургский технологический институт. В 1928 г. Борис Григорьевич был избран членом-корреспондентом, а в 1935 г. действительным членом Академии Наук СССР. Труды Б.Г.Галеркина относятся к проблемам строительной механики и теории упругости. Разработал методы решения дифференциальных уравнений теории упругости. С его именем неразрывно связан метод конечных элементов, применяемый

для численного решения дифференциальных уравнений в частных производных. Предложенная Б. Г. Галёркиным

формула решения уравнений уп-ругого равновесия, содержащая три бигармонические функции, позволила эффективно решить многие пространственные задачи теории упругости. Б. Г. Галёркин – один из создателей теории изгиба упругих пластин.

§8. Метод Ритца численного решения вариационной задачи

Рассмотрим следующий прямой метод приближенного решения вариационной задачи. Выберем функционал следующего вида: F[u] = (Lu,u) − 2( f ,u) , который определим на некотором линейном множестве

114

Ξ = {u}, где L – положительно-определенный линейный оператор; f –

заданная непрерывная функция. Предполагается, что функции класса Ξ удовлетворяют условиям R[u] = ϕ (P) , где R – известный линейный

функционал; ϕ – заданная функция. Построим последовательность достаточно гладких линейно независимых функций u0 (P), u1(P), K, un (P) , где u0 (P) удовлетворяет неоднородным краевым условиям R[u0 ] = ϕ (P) , а функции ui (P), i = 1, 2,K, n – однородным краевым условиям R[ui ] = 0, i =1, 2,K, n . Составим следующую линейную комбинацию:

u(P; c1, c2,

n

Так как R[u] = R[u0 ] + åci ×0 = ϕ

i=1

n

K, cn ) = u0 (P) + åciui (P) . (6.8.1)

i=1

(P), то u Ξ при любых постоянных

c1, c2,K, cn . Приближенное решение нашей вариационной задачи будем искать в виде (6.8.1). Для этого подставляем u(P; c1, c2,K, cn ) в выбранный функционал F[u] = (Lu,u) − 2( f ,u) и получаем

	F[u]= (c1 ,c2 ,K,cn ) ,	(6.8.2)
где	– известная функция, зависящая от n	переменных c1, c2,K, cn .

Подсчитываем коэффициенты c1, c2,K, cn таким образом, чтобы значение F [u] было минимальным. Это приводит к решению следующей системы уравнений:

	∂	=0,	∂	=0,...,	∂	=0.	Таким образом,	вариационная	задача приближенно
	∂c1		∂c2
				∂cn
сводится				к	задаче		об отыскании	безусловного	экстремума функции

(c1, c2 , K, cn ) .

Рассмотрим приведенную выше схему применительно к решению задачи

Дирихле для уравнений Лапласа:
u = 0, (x, y) G	(6.8.3)
u |∂G = f (x, y) ,	(6.8.4)

где ∂G – простой замкнутый контур, ограничивающий конечную область G , a

функция f (x, y) непрерывна на	∂G .		Данная		краевая задача		эквивалентна
следующей вариационной задаче для функционала:						ö2 ù
F[y] =	òò	éæ	¶u ö2	æ	¶u		(6.8.5)
		êç	÷	ç		÷
				+ ç	¶y	÷ ú dxdy ,
	G êè		¶x ø	è		ø ú
		ë				û

в классе функций, имеющих непрерывные частные производные до второго порядка включительно в замкнутой области G + ∂G и удовлетворяющих на границе ∂G краевому условию (6.8.4). Построим конечную систему линейно

независимых функций			(которые называются координатными		функциями)
u (x, y),	u (x, y), ...,	u	n	(x, y) C(2) (G + ∂G) , которые должны удовлетворять
0	1
условия на границе u0 (x, y) |∂G = f (x, y), ui (x, y) |∂G = 0, (i =1, 2,					..., n). Тогда
					115

линейная

комбинация

ϕ(x, y) = u0

n

принадлежит

классу

+ åciui (x, y) ,

i=1

допустимых функций при любых постоянных c1, c2,K, cn . Более коротко:

n

ϕ(x, y) = åciui (x, y),

(6.8.6)

i=0

где c0 = 1. Подставляя выражение (6.8.6) в функционал (6.8.5), получим

F [ϕ] = òò

n

∂ui )2

n

∂ui )2

[(åci

+ (åci

] dxdy .

(6.8.7)

G

i=0

∂x

i=0

∂y

Подберем коэффициенты c1, c2,K, cn так, чтобы функция

F [ϕ]

имела

минимум. Для этого требуется выполнение условий

∂

n

∂u j

∂u j

n

∂u j

∂u j

F[ϕ] = 2

òò[(åci

)

+ (åci

)

] dxdy = 0 , j

=1, 2, ...,

n ,

(6.8.8)

∂с j

∂x

∂x

∂y

∂y

G

i=0

i=0

что приводит к решению системы следующих алгебраических уравнений:

∂u

где [ui ,u j ] = òòG ( ∂xi

ì[u

0

,u ]+c [u ,u ]+...+c

n

[u

n

,u ] =0,

ï

1

1

1 1

1

ï[u0,u2 ]+c1[u1,u2 ]+...+cn[un ,u2 ] =0,

í

.....................................................

ï

ï[u

0

,u

n

]+c [u ,u

n

]+...+c

n

[u

n

,u

n

]=0,

î

1

1

∂u j

+

∂ui

∂u j

)dxdy

причем [ui ,u j ] = [u j ,ui ] .

∂x

∂y

∂y

(6.8.9)

Из линейной

системы (6.8.9) определяются коэффициенты c1, c2,K, cn .		Функция ϕ (x, y) и
будет	являться приближенным решением задачи	Дирихле. Точность

приближения зависит от выбора координатных функций uk (x, y) и от числа этих функций.

ИСТОРИЧЕСКАЯ СПРАВКА

Ритц Вальтер (Ritz Walter) (1878 – 1909) – знаменитый немецкий математик и физик-теоретик. Основные исследования

относятся к решению вариационных задач математической физики. Открыл спектральную формулу (формула Ритца).

Разработал идею вычисления частот непосредственно из энергетического функционала, без решения дифференциальных уравнений. Предложил (1908) мощный прямой метод приближенного решения вариационных задач – метод Ритца. Метод нашел широкое применение в теории колебаний, теории упругости, инженерной механике. Этот метод применяется для

приближённого решения вариационных задач и тех краевых задач математической физики, которые сводятся к вариационным. Строгое теоретическое обоснование метода Ритца дал в 1918 г. известный русский математик И. М. Крылов.

116

Пример. Найти функцию u = u(x, y), гармоническую в области G : x > 0, y > 0, x + y < 1 и удовлетворяющую на границе ∂G : x = 0, y = 0, x + y = 1 условию u | ∂G = x2 + y2 .

Решение. Выберем следующую систему координатных функций: u0 (x, y) = x2 + y2 , u1(x, y) = xy(1− x − y) ,

u2 (x, y) = x2 y(1− x − y) , u3(x, y)= xy2 (1−x− y)K

и составим линейную комбинацию

ϕ(x, y) = x2 + y2 + c1xy(1− x − y) + c2x2 y(1− x − y) + c3xy2 (1− x − y) . (6.8.10)

Легко проверить, что функция ϕ (x, y) удовлетворяет краевому условию ϕ | ∂G = x2 + y2 при любых значениях постоянных c1, c2, c3 .

Для составления системы (6.8.9) подсчитываем коэффициенты при неизвестных c1, c2, c3 и свободные члены:

[u0,u1] = [u1,u0 ] = òò[2x(y − 2xy − y2 + 2y(x − x2 − 2xy)]dxdy,

G

[u0,u2 ] = [u2,u0 ] = òò[2x(2xy − 3x2 y − 2xy2 ) + 2y(x2 − x3 − 2x2 y)]dxdy,

G

[u0 ,u3 ] = [u3 ,u0 ] = òò[2x( y2 − 2xy2 − y3 ) + 2y(2xy − 2x2 y − 3xy2 )]dxdy,

G

[u1,u1] = òò[(y − 2xy − y2 )2 + (x − x2 − 2xy)2 ]dxdy,

G

[u1,u2 ] = [u2 ,u1] = òò[(y − 2xy − y2 )(2xy − 3x2 y − 2xy2 ) +(x − x2 − 2xy)(x2 − x3 − 2x2 y)]dxdy,

G

[u1,u3 ] = [u3 ,u1] = òò[(y − 2xy − y2 )(y2 − 2xy2 − y3 ) +(x − x2 − 2xy)(2xy − 2x2 y − 3xy2 )]dxdy,

G

[u2 ,u2 ] = òò(2xy − 3x2 y − 2xy2 )2 + (x2 − x3 − 2x2 y)2 ]dxdy,

G

[u2 ,u3] = [u3,u2 ] = òò[(2xy − 3x2 y − 2xy2 )( y2 − 2xy2 − y3) +

G

+ (x2 − x3 − 2x2 y)(2xy − 2x2 y − 3xy2 ]dxdy,

[u3,u3] = òò[( y2	− 2xy2 − y3)2 + (2xy − 2x2 y − 3xy2 )2 ]dxdy.
G	= [u1,u1], a12 = [u1,u2 ], a13 = [u1,u3 ], a21 = [u2 ,u1],
Введём обозначения a11

a22 = [u2 ,u2 ], a23 = [u2 ,u3 ], a31 = [u3,u1] , a32 = [u3 ,u2 ], a33 = [u3 ,u3 ], b1 = [u0 ,u1],

b2 = [u0 ,u2 ],

b3 = [u0 ,u3 ].

Получаем

следующую

систему линейных

алгебраических

уравнений

(СЛАУ):

A × C = B , где

A = [ai j ,i =

1,3, j = 1,3] ,

C = [c ,c

2

,c

]T , B = [b ,b

2

,b ]T .

1

3

1

3

117

Значения коэффициентов при неизвестных c1, c2, c3 считает следующий

скрипт MatLab:

1.% подсчет коэффициентов при координатных функциях

2.syms x y u k;

3.% u(1),u(2),u(3),u(4) - система координатных функций

4.u(1) = x^2+y^2; u(2) = x*y*(1-x-y);

5.u(3) = x^2*y*(1-x-y); u(4) = x*y^2*(1-x-y);

6.% k - таблица коэффициентов при неизвестных

7.for i=1:4

8.for j=i:4

9.% k(j,i) = k(i,j) - элемент таблицы

10.k(j,i)=int(int(diff(u(i),'x')*diff(u(j),'x')+diff(u(i),'y')*diff(u(j),'y'),'y',0,1-x),'x',0,1);

11.k(i,j) = k(j,i);

12.end; end;

13.disp('Значения коэффициентов при неизвестных:');

14.disp(k);

Решив	систему,	находим	c1 ≈ 4,6667;	c2 = c3 ≈ −2,3333.	Подставляя
найденные	значения	величин	c1, c2, c3 в	формулу (6.8.9)	и получаем

приближенное формульное решение нашей задачи:

ϕ(x, y) = x2 + y2 + xy(1− x − y)[4,6667 − 2,3333(x + y)].

Следующий скрипт MatLab визуализирует полученное методом Ритца решение:

%визуализация решения, полученного методом Ритца

1.clear all;

2.format long;

3.x=[0:.02:1];

4.y=[0:.02:1];

5.[X,Y]=meshgrid(x,y); % задаём сетку

6.for i=1:length(x)

7.for j=1:length(y)

8.if (y(j)<=1-x(i)) % вычисляем значения, которые попадают в заданную область

9.Z(i,j)=x(i).^2+y(j).^2+x(i)*y(j)*(1-x(i)-y(j))...

10.*(4.6667-2.3333*(x(i)+y(j)));

11.else

12.Z(i,j)=NaN;

13.end; end; end;

14.surf(X,Y,Z); % визуализируем решение

15.title ('\bfRitc method') % заголовок графика

16.xlabel('x'); ylabel('y'); zlabel('z(x,y)'); v = axis; % границы осей

17.da = daspect; % масштаб осей

18.da(1:2) = min(da(1:2)); % min из двух

19.daspect(da) % выравняли масштаб осей

20.axis(v); % оставили границы

21.colormap(gray) % выбрали палитру

22.grid on % показали сетку

23.box on % показали внешний контур

118

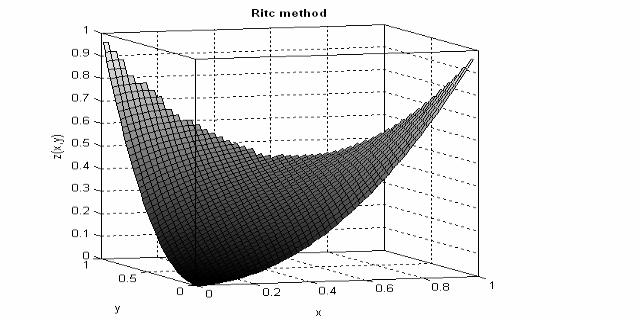
График полученного решения совпадает с графиком, приведенным в §4:

119