t
X (t)=F(t)×F −1(t0 )×X0 +òF(t)×F −1(τ )× f (τ )dτ .	(1.3.8)
t0
В силу теоремы о существовании и единственности	решения

дифференциальной системы, получаем следующее представление для структуры матрицы Коши:

F(t,τ ) = F(t) × F −1(τ ) .

(1.3.9)

ИСТОРИЧЕСКАЯ СПРАВКА

Лагранж Жозеф Луи (Lagrange Joseph Louis) (1736 – 1813) – великий французский математик и механик. Член Парижской Академии Наук, член Берлинской Академии Наук. С 1795 г. был профессором Нормальной школы, с 1797 г. – Политехнической школы. Наиболее важные

труды Лагранжа относятся к вариационному исчислению и аналитической механике. Разработал основные понятия вариационного исчисления, предложил фундаментальный аналитический метод – метод вариаций решения бесконечномерных экстремальных задач. Лагранжу

принадлежат выдающиеся результаты в области математического анализа – формула остаточного члена ряда Тейлора, формула конечных приращений, теория

условных экстремумов конечномерных экстремальных задач. В теории дифференциальных уравнений им построена общая теория особых решений, предложен фундаментальный метод

вариации произвольных постоянных решения нелинейных обыкновенных дифференциальных уравнений и систем уравнений.

§4. Пример использования формулы Коши

Рассмотрим следующее дифференциальное уравнение с дополни-

тельными условиями:	¶2 x	= x + t ,	¶ x(0)	=1, x(0) = 1. Сведем его к задаче Коши
	¶t 2		¶t

для следующей системы дифференциальных уравнений:

ì¶ x = y, ïï ¶t

íï¶ y = x + t, ïî ¶t

ìx(0)=1, íîy(0)=1.

Перепишем систему в матричном виде:

é d

X 1

(t )

ù

éX1

(0) ù

é1ù

ê dt

ú

é0 1

ù

é X

1 (t ) ù

é0

ù

=

êX

(0)ú

.

ê

d

ú

= ê

ú

× ê

ú

+ ê

ú

ê1ú

ê

X 2

(t )

ú

ë1 0

û

ë X

2 (t )û

ët

û

ë

2

û ë û

ê

ú

ë dt

û

Решим ее

по

формуле

Коши.

Для

этого

подсчитаем матрицу

F(t,τ ) = F(t) × F −1(τ ) ,

F(t)

– составлено из векторов ФСР.

Выпишем общее

решение, соответствующее однородной системе уравнений, т.е. найдем векторы ФСР.

11

Общее решение вычисляется через собственные числа и

соответствующие им векторы матрицы A. Получаем:	A× x = λx; Ax - λEx = 0 ;
(A − λ E) x = 0 ; det(A − λE) = 0 . Отсюда: λ2 -1 = 0,	λ1 = 1, λ2 = −1. Найдем

собственный вектор x1 , соответствующий собственному значению λ1 . Для этого

решаем систему линейных алгебраических уравнений (A − л1 E)x1								= 0 . Получаем
x1	é1ù	« λ1	=1.	Для второго вектора аналогично:	x2	=	é	− 1ù	« λ2	= -1.
	= ê ú						ê	ú
	ë1û						ë	1û

Выписываем общее решение соответствующей однородной дифференциальной

системы: x(t) = c

×

é

1ù

× et + c

2

×

é

− 1ù

× e−t .

Переписываем

в

матричной форме

1

ê

ú

ê

ú

ë

1û

ë

1û

éet - e−t ù

éc

ù

относительно c1

и

c2 и

получаем:

х(t) = êet

e−t ú

1

ú . Следовательно,

× êc

ë

û

ë

2

û

	éet - e−t ù				и F −1 (τ ) =	1	é	e−τ
	F(t) = ê	t		−t ú			× ê	τ
			e			2
	ëe			û			ë- e

	получаем	F(t,τ ) =	1	éet−τ + e−(t−τ )
				× ê
			2
				êet−τ - e−(t−τ )
				ë

e−τ ù		. Поскольку F(t,τ ) = F(t) × F −1(τ ) , то
τ	ú
e	û
et−τ - e−(t−τ ) ù
et−τ		ú . Таким образом, матрица
		+ e−(t −τ ) ú
		û

F(t,τ ) Коши (Грина) построена	и можно применить формулу Коши
t		= êé1úù , окончательно
X (t) = F(t,t0 ) × X0 + ò F(t,τ ) × f (τ )dτ .	С учетом того что X0
t0		ë1û

получаем формульное решение задачи Коши:

éX 1(t) ù = êëX 2(t)úû

1

2

é

t

+e

−t

e

t

-e

−t ù

é1ù

t é

e

t−τ

+e

−(t−τ )

e

1

ò

×ê

ú

×ê ú+

×ê

-e−t

2

-e−(t−τ )

êet

et +e−t ú ë1û

êet−τ

ë

û

0

ë

éX

1 (t)ù

=

éet ù

+

t

é- 2 + et + e−t

ê

ú

ê ú

ê

et - e−t

2

ëX

2 (t)û

ëet û

ë

et−τ -e−(t−τ ) ù é0ù

et−τ +e−(t−τ ) úú×êët úûdτ

û

ùú .

û

Приведем скрипт в среде MATLAB построения матрицы F(t).

1.%начальные условия

2.A=[0 1;1 0];

3.syms lmd t temp x1 x2;

4.%поиск собств. значений матрицы A

5.ASymb=sym(A);

6.for i=1:1:2

7.ASymb(i,i)=ASymb(i,i)-lmd;

8.end;

9.self_v=solve(det(ASymb));

10.%формируем матрицы частных решений: решение уравнения (A-v*E)*x=0

11.E=eye(2,2);

12.Z=[0;0];

13.%поиск частного решения X1

14.K1=A-self_v(1)*E;

15.tX1=sym(K1)*[x1;x2];

12

16.X1=K1\Z;

17.ta1=K1(1,:)+K1(2,:);

18.if(ta1(1)*ta1(2)==0)

19.X1=~double(ta1);

20.else

21.X1(1)=1; X1(2)=subs(solve(tX1(1),x2),x1,1); end;

22.%поиск частного решения X2

23.K2=A-self_v(2)*E;

24.tX2=sym(K2)*[x1;x2];

25.X2=K2\Z;

26.ta2=K2(1,:)+K2(2,:);

27.if(ta2(1)*ta2(2)==0)

28.X2=~double(ta2);

29.else

30.X2(1)=1; X2(2)=subs(solve(tX2(1),x2),x1,1); end;

31.%формируем матрицу F(t) из частных решений X1 и X2

32.Ft=sym(zeros(2));

33.Ft(:,1)=X1*exp(self_v(1)*t);

34.Ft(:,2)=X2*exp(self_v(2)*t);

35.%упрощаем и выводим

36.Ft=simplify(Ft); disp('F(t) ='); disp(Ft);

ИСТОРИЧЕСКАЯ СПРАВКА

Моулер Клив (Moler Cleve Barry) – знаменитый

специалист в области прикладного численного программирования. Специализируется на мате- матических проблемах численного анализа. Является председателем компании MathWorks Incorporated. Около двадцати лет работал

профессором математики и информатики в университете Мичиган, Стэндфордском уни- верситете и университете Нью-Мексико. В конце 1970-х годов Клив Моулер разработал пакет численных методов MATLAB. Вскоре новая среда

быстро распространилась среди других университетов США. В настоящее время

MATLAB является мощной средой численной и символьной математики, включающей в себя средства структурного, объектного и визуального программирования, оснащенной мощными конверторами и специализированными инструментариями ToolBox. В 1997 г. Клив Моулер был избран в Национальную Инженерную Академию США. В январе 2007 г. Клив Моулер вступил в должность президента СИАМ (SIAM).

§5. Понятие о методе прямых

Кратко рассмотрим эффективный подход, позволяющий сводить краевые

задачи для линейных дифференциальных уравнений в частных производных к исследованию линейных дифференциальных систем (1.1.3) первого порядка.

Пусть в плоскости Oxy (см. рисунок) задана трапециевидная область G,

основания которой лежат на прямых y = α и	y = β , (α < β ) , а по бокам эта
область ограничена аналитическими кривыми	x = g0 (y) (L) ,	x = g1( y) (Г) ,
(α ≤ y ≤ β; g0 ( y) < g1 (y)). Пусть область	G целиком	помещается в
		13

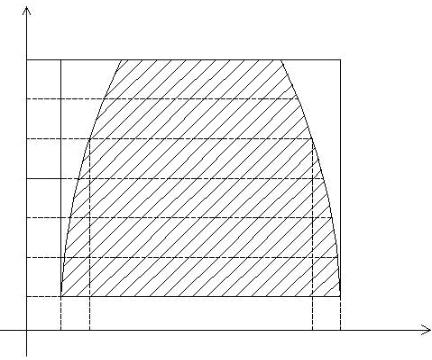
минимальном прямоугольнике R = { (x, y) :a ≤ x ≤ b;α ≤ y ≤ β }. В области G требуется найти решение u = u(x, y) линейного дифференциального уравнения

	A ( x , y )	∂ 2 u	+ 2 B ( x , y )	∂ 2 u	+ C ( x , y )	∂ 2 u	+
		∂ x 2		∂ x ∂ y		∂ y 2

	+ a(x, y)	∂u	+ b(x, y)		∂u	+ c(x, y)u = f (x, y) ,		(1.5.1)
		∂x			∂y
	которое удовлетворяет на границе области G следующим краевым условиям:
	u(x;α ) = ϕ0 (x),u(x, β ) = ϕ1(x),			u(g0 ( y), y) =ψ 0 ( y),u(g1( y), y) =ψ1( y) .				(1.5.2)
	x
	β − yn						R
	M j					G	N j
	y j
	L						Г

y1

α − y0

0

a x j

j b

y

x

Будем предполагать, что коэффициенты и правая часть уравнения (1.5.1)

определены и аналитичны в замкнутом прямоугольнике R, причём

A(x, y) ¹ 0,C(x, y) ¹ 0,

(x, y)Î R .

(1.5.3)

Допустим также, что функции ϕ0 (x) и ϕ1(x) являются аналитическими на

всём отрезке

[a,b] , а функции ψ 0 ( y) и ψ1 (y)

– аналитическими на отрезке

[α,β ]

и выполнены условия согласованности:

ϕ0 (g j (α )) =ψ j (α ) ,ϕ1 (g j (β )) =ψ j (β ) , j =0,1.

(1.5.4)

Для получения по методу прямых приближённого решения краевой

задачи (1.5.1) – (1.5.2) разделим отрезок [α,β ]

на n равных частей с помощью

точек

y

j

= y

+ jh (y

0

= α, y

n

= β ) ,

h = β − α ,

j =0,1,2,...,n и

через внутренние

0

n

точки деления проведём семейство параллельных прямых

y = y j , j =0,1,2,...,n−1.

На каждой такой прямой дифференциальное уравнение (1.5.1) приближенно

заменим обыкновенным дифференциальным уравнением для искомых функций u(x, yj ) . Для этого в (1.5.1) избавимся от частного дифференцирования по y с

помощью формул численного дифференцирования:

14

∂u ∂y

≈	1	[u(x,y j+1) − u(x, yj−1)],	∂2u		≈	1	[u′x (x,y j+1) − u′x (x, yj−1)],
	2h		∂x∂y			2h
y= y j					y= y j

∂2u

≈

1

[u(x,y

j+1

) − 2u(x, y

) + u(x, y

−1

)],

j = 1, 2, ..., n −1.

(1.5.5)

∂y2

h2

j

y=y j

j

∂u(x, yj )

= u′j (x) ,

∂2u(x, yj )

= u′j′(x),

Введём обозначения: u(x, yj ) = uj

(x) ,

∂x

∂x2

A(x, yj ) = Aj (x) , … Тогда подставляя выражения (1.5.5) в уравнение (1.5.1), получим следующую систему обыкновенных дифференциальных уравнений:

Aj (x)u′j′(x) +	Bj (x)		[u′j+1(x) − u′j−1 (x)]				+	Cj (x)	[uj+1 (x) − 2uj (x) + uj−1(x)] +
		h						h2
+ aj (x)u′j (x) +		bj (x)		[uj+1(x) − uj−1(x)] + aj (x)uj (x) = f j (x), j =0,1,2,...,n−1.						(1.5.6)
		2h
Кроме того, в силу краевых условий (1.5.2) получаем
						u0 (x) = ϕ0 (x) , un (x) = ϕ1 (x)				(1.5.7)
				′	′	′		′	(x) .
и, следовательно, u0 (x) = ϕ0						(x) , un	(x) = ϕ1
Таким	образом,				от линейного дифференциального уравнения					(1.5.1) с

частными производными мы перешли к системе (1.5.6) из n−1 обыкновенных дифференциальных уравнений с n−1 неизвестными функциями u1(x),u2 (x),...,un−1(x) , где u0 (x) и un (x) определяются формулами (1.5.7).

Так как коэффициенты и правые части линейной системы (1.5.6) аналитичны, а следовательно, непрерывны на отрезке [a,b] , старшие

коэффициенты	Aj (x) ¹ 0 ,	a ≤ x ≤ b ,	то	общее	решение
uj (x) =ϕ j (x;C1,C2 ,...,C2n−2 ) , j =1,2,...,n−1 системы (1.5.6)				определено на отрезке

[a,b] и содержит 2n−2 произвольных постоянных C1,C2,...,C2n−2 , входящих в функции ϕi линейно.

		y	y = yj+1
			M j	y = yj		N j
						y = y j−1
		0 x j+1	xj 1 x j	x j−1	x	j	x	j−1	x
			+
		Для определения этих постоянных из краевых условий (1.5.2) получаем
такое же число линейных алгебраических уравнений.							Пусть		x j = g0 (yj ) и
		j = g1(yj ) – проекция на ось Ox концов отрезка M j N j					, лежащего на прямой
	x

y = yj . Тогда на основании формул (1.5.2) получаем граничные условия:

15

uj (x j ) =ψ 0 ( yj ) ,uj (

x

j ) =ψ1 (yj ) , a ≤ x j <

x

j ≤ b,( j =1,2,...,n −1) .

(1.5.8)

Таким образом, задача (1.5.1) – (1.5.2) сводится к решению краевой задачи (1.5.6) – (1.5.8) для системы обыкновенных дифференциальных уравнений. Решение задачи (1.5.6) – (1.5.8) может быть выражено формульно или получено с помощью приближённых методов. Причём функции uj (x)

должны определяться на всём отрезке [a,b] . После этого мы будем знать приближённые значения искомой функции u(x, y) на семействе параллелей

y = y j , j =0,1,2,...,n . Значения функции u(x, y) в промежуточных точках области G
могут быть найдены методами интерполирования.
Отметим следующую особенность краевой задачи (1.5.6) – (1.5.8).
Каждую из искомых функций uj (x) нужно определить на всём отрезке [a,b] ,
зная её значения в двух, вообще говоря, внутренних точках x j и x j	этого
отрезка. Если мы найдём некоторую функцию uj (x) лишь при x j ≤ x ≤ x j	, этого

может оказаться недостаточным для решения задачи, поскольку проекция на

ось Ох отрезка M j N j

прямой

y = yj (x j ≤ x ≤

x

j )

в общем случае не покрывает

проекций

на

эту

ось

соседних

прямых y = yj−1(x j−1 ≤ x ≤

j−1)

и

x

y = yj+1 (x j+1≤ x ≤

j+1) .

В

этом

случае для

нахождения из системы (1.5.6)

x

функций

uj−1(x)

и

uj+1 (x) нужно знать значения функции uj (x) вне отрезка

[x j ,

j ] .

x

Пример 1. Исследование параболической системы методом прямых

Пусть в

области

R = { (x,t),

0 < x < 3; 0 < t < 3} задано неоднородное

параболическое уравнение вида ∂u =

∂2u

+ x + t , удовлетворяющее начальному

u(x,0) = 0

∂t

∂x2

u(0,t) = 0, u(3,t) = 0. Методом

условию

и

граничным

условиям

прямых найдем решение данного уравнения.

Положим для простоты h =1 и

проведём

прямые

x =1

и

x = 2. Используя

метод прямых, будем искать

приближённое решение uj (t) = u(t, xj ) , j =1,2

на прямых x = x1 =1 и x = x2

= 2 .

Избавляясь от частных производных по

x

с помощью формулы численного

дифференцирования:

¶2u

[u(t,x j+1)-2u(t,x j )+u(t,x j−1)], j =1,2 , получаем систему

»

1

¶x2

x=x

j

h2

ìu¢(t) = u

(t) - 2u (t) + u

(t) + t +1,

í

1

0

1

2

îu2¢ (t) = u1(t) - 2u2 (t) + u3 (t) + t + 2.

Из краевых условий следует, что

u0 (t) = u3 (t) = 0 . Поэтому система

запишется в следующем виде:

ìu¢(t) = -2u (t) + u

(t) + t +1,

í 1

1

2

îu2¢ (t) = u1(t) - 2u2 (t) + t + 2.

16

Краевые условия преобразуются следующим образом: u1(t) = u2 (t) = 0. Переписывая в матричной форме, окончательно получаем

ì d		U (t) = A×
ï
ídt
ï
îU (t0 ) =U0 ,
где приняты обозначения		é- 2
		A = ê
		ë 1

U (t) + F(t),

	1 ù		– матрица коэффициентов,
	- 2	ú
		û

éu1 (t)ù

é t + 1 ù

, U (t

éu

(0) ù

, U 0

é0ù

U (t) = êu

(t)ú

– вектор переменных,

F (t ) = êt + 2

ú

0 ) = êu

1

(0)

ú

= ê

0

ú .

ë 2

û

ë

û

ë

2

û

ë

û

Таким образом, исследование параболического уравнения с

соответствующими начальным и граничными условиями свелось к исследованию системы линейных обыкновенных неоднородных дифференциальных уравнений первого порядка. Используем формулу Коши

(1.2.7).

Пример 2. Исследование гиперболической системы методом прямых

Пусть в области R = { (x,t), 0 < x < 3;0 < t < 3} задано неоднородное

гиперболическое уравнение вида:	¶2u	-	¶2u	= x + t , удовлетворяющее
	¶t2		¶x2

ìu(0,t)

граничным í

îu(3,t)

= 0,		ìu(x,0) = u					t=0 = x,
	и начальным условиям	íï	¶u				Методом прямых
= 0		ï	¶t		= x.
		î			t=0

найдем решение этого уравнения.

Положим h =1 и проведём прямые

x =1 и

x = 2. Будем искать приближённое решение uj (t) = u(t, xj ) ,

j =1,2

на прямых

x = x1 =1 и x = x2

= 2 . Получим систему в матричной форме:

¶2

¶2

éu(t, x1)ù

ét + x1

ù

U (t, xj ) =

U (t, xj ) + F(t, xj ) U (t, xj ) = ê

ú

, F(t, xj ) = ê

ú .

¶t

2

¶x

2

,

ëu(t, x2 )û

ët + x2

û

¶2u

Избавляясь

от дифференцирования

по

x с

помощью

формулы

»

1

[u(t,x j+1)-2u(t,x j )+u(t,x j−1)], j =1,2 , с учетом условий u(0,t) = u(3,t) = 0 ,

¶x2

x=x

j

h2

¢¢

Либо то же самое в матричной форме:

получаем íìu1(t) = -2u1(t) + u2 (t) + t +1,

îu2¢¢(t) = u1(t) - 2u2 (t) + t + 2.

d

2

U(t) = A×U(t) + F(t),

dt2

é- 2

1

ù

,

éu

(t ) ù

, F (t) =

é t + 1

ù

A = ê

- 2

ú

U (t ) = ê 1

ú

ê

ú .

ë 1

û

ëu 2 (t )û

ët + 2

û

Причем данное уравнение будет иметь следующие начальные условия:

17

éu (0)ù

é1

ù

é d

u (0)

ù

1

U 0= U (t0 ) = U (t)

0¢ = d U (t)

ê

ú

t =0

= ê

ú =

ê ú , U

1

= ê dt

1

ú

= é ù .

0

ëu2

(0)û

ë2û

t0 =0

d

ê

ú

dt

ê

u

(0)ú

ë

2û

2

ë dt

û

ì

d

2

U (t) = A×U (t) + F(t),

ï

2

ïdt

Таким образом, получили систему: íU (t0 ) =U0 ,

ï d

ï

¢

ï

U (t0 ) = U0.

îdt

К полученной системе вновь можно применить метод прямых по t и

избавиться от второй производной

d 2

U (t) , оставив

первую

d

U (t) , и

dt2

dt

получим систему первого порядка. Но поступим иначе. Введем новые перемен-

ные: u1′(x) = u3 (x) , u′2 (x) = u4 (x) , u3′ (x) = -2u1 (x)+u2 (x)+t +1 , u4′ (x)=u1(x)-2u2 (x)+t+2 .

С учетом введенных обозначений получаем систему первого порядка:

é 0 ~ ê 0

A = êê- 2 êë 1

0	1	0ù
0	0	1	ú
			ú ,

10 0ú

-2 0 0úû

	ì d			~
	ï		U (t
		dt
	í
		~
	ï
	U (t0 )
	î
	éu1			(t)
~	êu		2	(t)
U (t) = ê				(t)
	êu		3
	ê			(t)
	ëu4

	~ ~	~
)= A×U (t)+F(t),
	~	,		где
	=U0
t0=0
ù		é	0	ù		éu1 (0)	ù		é	1ù
ú	~	ê	0	ú	~	êu2 (0)	ú	~	ê	2ú
ú	, F (t)	= ê	+ 1	ú	,U (t0 ) = ê		ú	, U0	= ê	ú .
ú		êt		ú		êu3 (0)	ú		ê	1ú
ú		ê		ú		ê	ú		ê	ú
û		ët	+ 2û			ëu4 (0)	û		ë	2û

Далее данная система исследуется как система линейных обыкновенных неоднородных дифференциальных уравнений первого порядка с помощью формулы (1.2.7).

Замечание. Несмотря на кажущуюся простоту метода прямых, для

корректного численного исследования системы нужно постоянно учитывать погрешности приближения численного дифференцирования.

18