Cформулируем следующую задачу. Среди функций u = u(x, y), удовлетворяющих вышеперечисленным условиям, найти такую u(x, y), которая

доставляет минимум функционалу вида (2.7.1). Геометрически это означает, что сравниваются между собой всевозможные поверхности вида u = u(x, y) и

«натянутые» на один и тот же контур ∂G , ограничивающий область G . Таким образом, задача вариационного исчисления имеет вид

J (u)=

æ

,¶u

ö

®min,

ü

òò

Fç x, y,u(x,y),¶u

÷dxdy

ï

ç

¶x

¶y

÷

G

è

ø

ï

(2.7.2)

ý

u(x, y)

(x, y)ζG

=ϕ(x,y).

ï

ï

þ

Если на

допустимой

поверхности u(x, y)

(поверхности, подчиненной

ограничениям

на ¶G ), удовлетворяющей

условию

~

≤ ε ,

u (x, y) − u(x, y)

(x, y) G выполняется

~

то

говорят,

что функционал J (u (x, y))

J (u ) ³ J (u) ,

(2.7.2) достигает на (x, y) G сильного минимума.

§8. Вариация поверхности. Вариация функционала

Пусть на минимум исследуется допустимая поверхность, которая удовлетворяет граничным условиям. Другие допустимые поверхности можно

представить в виде

~

(2.8.1)

u (x, y) =u (x, y) +ε h(x, y),

h(x, y)

(x, y) ∂G

≡ 0 .

(2.8.2)

~

Пусть

– некоторая

функция, полученная из

u (x, y) = u(x, y) + ε h(x, y)

заданной функции u(x, y) . Функцию

δ (u(x, y)) = ε h(x, y) назовём вариацией

допустимой поверхности u(x, y) .

Вариация δ J (u)

нелинейного функционала

J (u) – это главная линейная часть его приращения J (u)

при переходе от

~

= u(x, y) + ε h(x, y).

u(x, y) к близкой функции u (x, y)

При переходе от u(x, y)

к

~

функционал

(2.7.1) получит

u (x, y)

приращение

~

~

~

J (u) = J (u ) − J (u) = òòF(u )dxdy − òòF(u)dxdy = òò

(F(u ) − F(u))dxdy .

G

G

G

С учётом представления (2.8.1)

приращение функционала

J (u) может

быть представлено в следующем виде:

J (u) = òò

~

(F (u ) − F (u))dxdy =

òò

G

x

y

y

x

y

=

x

)) dxdy

=

( F ( x , y ,u + ε h ,u ′ + ε h

′

,u ′

+ ε h ′ ) − F ( x , y ,u ,u ′

,u ′

G

é

1

2 F ( x, y,u,u¢x ,u¢y ) +o(ε 2 ) ;

= êDF ( x, y,u,u¢x ,u¢y ) = dF ( x, y,u,u¢x ,u¢y ) +

d

2

ë

31

æ

¶ F

¶ F

¶ F

ö

;

dF ( x , y , u , u ¢

, u ¢ ) =

ç

h +

h

x

+

h

÷

ε

x

y

ç

¶ u

¶ u ¢x

¶ u ¢y

y ÷

è

ø

12 d 2 F (x, y,u,u¢x ,u¢y ) =

+ε 2

2

æ

¶

2

F

¶

2

F

¶

2

F

¶

2

F

¶

2

F

¶

2

F

ö

ε

2 ù

ç

2

¢

2

¢

2

¢

¢

¢ ¢

÷

ú

=

ç

¶u2 h

+ ¶(u¢ )2

(hx )

+¶(u¢ )2

(hy )

+2

¶u¶u¢x hhx

+2

¶u¶u¢y hhy +2

¶u¢x¶u¢y hxhy

÷

2 ú

=

è

x

y

ø

û

æ

¶F

¶F

¶F

ö

ε 2

¶ 2 F

2

ç

h +

h x

+

÷

+

òò

2

h

dxdy

+

= ε òò ç

¶u

¶u ¢x

¶u ¢y

h y ÷ dxdy

2

¶u

G

è

ø

G

æ

¶2 F

2

¶2 F

2

¶2F

¶2 F

¶2 F

ö

ç

÷

¢

¢

¢

¢

¢

¢

òò

ç

¶(u¢x )

2 (hx ) +

¶(u¢y )

2 (hy )

+ 2

¶u¶u¢x

hhx

+ 2

¶u¶u¢y

hhy

+

2

hxhy

÷dxdy +

G

è

¶u¢x¶u¢y

ø

+ o(ε 2 ) .

Вводя

обозначения

δJ для

первой и

δ 2 J

для

второй

вариаций

функционала J (u):

æ

¶F

¶F

¶F

ö

δJ = òò

ç

h +

hx

+

÷

(2.8.3)

ç

¶u

¶u¢x

¶u

hy ÷dxdy ,

G

è

¢y

ø

2

2

æ

2

F 2

2

F

¢

2

2

F

¢

2

2

F

¢

2

F

¢

2

F

ö

ç

¶

¶

¶

¶

¶

¶

¢ ¢ ÷

δ

J =òòd

F =òòç

2 h +

(hx )

+

(hy )

+2

hhx +

hhy +

hxhy ÷dxdy

,

¶u

¶(u¢x)

2

¶(u¢y )

2

¶u¶u¢x

¶u¶u¢y

¶u¢x¶u¢y

G

G è

ø

получаем, что приращение функционала

J (u) является функцией числового

параметра ε и может быть представлено в виде: DJ(u) =ε δ J+ 12ε2δ 2J + o(ε2 ) .

Для фактического подсчёта δ J и δ 2 J								удобно использовать следующие
формулы:	δ J =	d	J (u+ε h)			δ 2 J =	d 2	J (u + ε h)		.	Действительно,
					;
		dε					dε 2
					→0					е→0

подсчитаем первую вариацию функционала J (u) по формуле и сравним с известным результатом (2.8.3):

δJ = ddε (J (u + εh)) ε →0 = ddε òòG F (x, y,u + εh,u¢x + εhx¢,u¢y +

вышеприведенной

εh¢y )dxdy =

ε →0

= òò

d

′

′

′

′

)dxdy

=

dε

F ( x, y , u + εh, u x

+ εhx

, u y

+ εhy

G

=

òò

d

F ( x , y , u , u ¢x , u ¢y ) dxdy

=

ε → 0

d ε

G

)hx + Fu′y (x, y,u,u x ,u

)hy )dxdy .

= òò(Fu (x, y,u,u x ,u y )h + Fu′x (x, y,u,u x ,u

¢

¢

¢

¢

¢ ¢

¢

¢

¢

¢

¢

G

′y h y ) dxdy .

То есть получили уже знакомую формулу δ J = òò ( Fu h + Fu ′x hx + Fu

′

′

′

′

′

G

32

§9. Уравнение Остроградского

Решение вариационной задачи (2.7.2) возможно только вдоль тех

поверхностей, на			которых				первая вариация	δ J (u) функционала
J (u)=	òò	æ	¶u	,	¶u	ö	обращается в нуль,	т.е. δ J (u)= 0, h(x, y) ,
		ç				÷
		Fç x, y,u(x, y),				÷dxdy
	G	è	¶x		¶y	ø

удовлетворяющих (2.8.2). Получим дифференциальное уравнение, решение

которого

u = u(x, y)

превращает

в

нуль

первую

вариацию

функционала:

δ J (u)=0 .

δJ (u ) =

æ

¶F ( x, y , u , u ¢x , u ¢y )

¶F ( x, y , u , u ¢x

, u ¢y )

¶F ( x, y , u , u ¢x , u ¢y )

ö

ç

h +

¢

+

¢ ÷

=

= òò ç

¶u

¶u ¢x

hx

¶u ¢y

hy ÷dxdy

G è

ø

é

é

¶

æ

¶ F

ö ù

ê

êu = F

¢

′

¢

, du =

ç

÷

ú

= ê

ò

¢

¢

u x

ç

¢

÷

=

Fu

′ h x dx =

ê

¶ x è

¶ u x

ø

ú

ê

x

ê

¢

ú

ë

ë dv =

h x dx , v = h

û

¶

æ

¶ F

ö

- ò h

¶

æ

¶ F

ö

=

ç

÷

ç

÷

ç

÷ h

¶ x

ç

¶ u ¢x

÷dx ;

¶ x è

¶ u ¢x ø

è

ø

é

¶

æ

¶ F

ö

ù

ê u = Fu¢ ′

h ¢y , du =

ç

÷

ú

ò Fu¢ ′y h ¢y dy = ê

y

¶ y

ç

÷

ú =

è ¶ u ¢y

ø

ê

= h ¢y dy , v = h

ú

ê dv

ú

ë

û

¶

æ

¶ F

ö

¶

æ

¶ F

ö

ù

=

ç

÷ h - ò h

ç

÷dy ú =

¶ y

¶ u ¢y

¶ y

¶ u ¢y

ç

÷

ç

÷

ú

è

ø

è

ø

û

h )dxdy

æ

¶

æ

¶F

ö

ö

¢

ç

¢

-

h

ç

÷

÷

+

= òò (Fu

+ ò

ç

Fu ′

h

G

ò

¶x

ç

¶u ¢x

÷dx

÷dy

G

G y

è

x

G x

è

ø

ø

	æ						¶	æ
+ ò	ç	Fu¢′y	h			- òh		ç
	ç				G		¶y ç
G x è								è

Из условия (2.8.2) следует, что h ∂ G перепишем в следующем виде:

	¶F	ö	ö
		÷dy ÷dx = 0 .
	¢
		÷	÷
	¶u y	ø	ø

= 0 , поэтому полученный результат

¶

æ

¶F ö

¶

æ

¶F

ö

ç

÷

òò

¢

òò

ç

÷

òò

ç

÷

δJ (u ) =

(Fu h )dxdy

-

h

ç

÷

dxdy -

h

dxdy

=

G

G

¶x è

¶u ¢x ø

G

¶y è

¶u ¢y ø

æ

¶

æ

¶ F

ö

¶

æ

¶ F

ö ö

(2.9.1)

= òò

ç

¢

ç

÷

ç

÷ ÷

h

ç

F u

-

ç

¶ u

¢

÷

-

¶ y

ç

¢

÷ ÷ dxdy

= 0 .

G

è

¶ x è

x

ø

è

¶ u y

ø ø

Из формулы (2.9.1) в силу произвольного выбора

h ,

не равного нулю,

сразу следует формула

¶F

¶

æ

¶F

ö

æ

¶F

ö

-

ç

÷

¶

ç

÷

= 0.

(2.9.2)

¶u

ç

÷-

ç

÷

¶x è

¶ux ø

¶y è

¶u y ø

33

Уравнение (2.9.2) – нелинейное уравнение в частных производных второго порядка с непостоянными коэффициентами. Оно называется уравнением Остроградского (было впервые получено М. В. Остроградским в 1834 г.).

Выпишем уравнение Остроградского в развернутой форме:

¶ F

æ

¶ 2 F

¶ 2 F ¶ u

¶ 2 F

¶ u ¢

¶ 2 F ¶ u ¢y

ö

- ç

+

+

x

+

÷

-

¶ u

ç

¶ x ¶ u

¢x

¶ u ¶ u ¢x ¶ x ¶ u ¢x ¶ u ¢x ¶ x

¶ u ¢y ¶ u ¢x ¶ x

÷

è

ø

æ

¶

2 F

¶

2 F ¶ u

¶ 2 F

¶ u ¢y

¶ 2 F ¶ u ¢

ö

- ç

+

+

+

x

÷

= 0

.

ç

¶ y ¶ u ¢y

¶ u ¶ u ¢y ¶ y ¶ u ¢y ¶ u ¢y ¶ y

¶ u ¢x ¶ u ¢y ¶ y

÷

è

ø

Искомая функция u(x, y) определяется как решение уравнения

Остроградского и дополнительно должна удовлетворять условию вдоль границы u(x, y)(x, y)ζG = ϕ(x, y) .

Для того чтобы поверхность u(x, y),(x, y) G , u(x, y)(x, y)ζG = ϕ(x, y) доставляла сильный минимум функционалу J = J (x, y,u,ux' ,uy' ), необходимо, чтобы u(x, y) удовлетворяла условию Остроградского (2.9.2).

Задачи для решения. Составить и решить уравнение Остроградского для следующих функционалов:

òò(ux2 + uy2

+ 2xyu)dxdy ® min; G :

ì0 £ x £ 2;

¶G =

x

2

+

y

2

1.

í

.

50

100

G

î0 £ y £1;

òò(3ux2 + uy2

+ 2xucos y)dxdy ® min;

G :

ì 0 £ x £ 2;

¶G =

x

2

-

y

.

2.

í

£ y £1;

200

100

G

î-1

æ

2

2

+ 2usinπxsin

πy ö

ì0 £ x £1;

x2 - 2y

3.

òòç

3ux - uy

÷dxdy ® min;

G :

í

£ y £ 2;

¶G =

.

2

200

G è

ø

î0

òò(ux2 - 2uy2

+ 2xusinπy)dxdy ® min;

G :

ì0 £ x £ 2;

¶G =

x

2

-

y

.

4.

í

1;

200

50

G

î0 £ y £

òò(ux2 + 2uy2

+ u2

+ 2xu cos y)dxdy ® min;

G :

ì

0 £ x £ 2;

¶G =

x

2

-

y

.

5.

í

£ y £1;

100

60

G

î-1

òò(2ux2 + uy2

+ u2

+ 2yucos x)dxdy ® min;

G :

ì-1£ x £1;

¶G =

x

2

+

y

.

6.

í

0 £ y £1;

100

60

G

î

òò(ux2 + 5uy2

+ u2

+ 2x2 yu)dxdy ® min;

G :

ì0 £ x £ 2;

¶G =

x

+

y

2

.

7.

í

£ y £ 2;

160

G

î0

100

Приведем скрипт в среде MATLAB решения данной задачи, используя инструментарий ToolBox PDE (Partial Differential Equations).

	æ	2	2	æ	x öö
	Решаем вариационную задачу J (z)= òòçux		- 2uy	+ 2yuçsinπx +		÷÷dxdy ® min;
					5
	G è			è		øø
	34

ì0

£ x £1;

x

y

2

∂u

∂u .

G : í

¶G =

+

.

Введем обозначения: u = u(x, y), p =

,q =

y £

2;

¶x

î0

£

10 50

¶y

1.syms x y u Dux Duy D2ux2 D2uxy D2uy2 % переменные

2.F = Dux^2-2*Duy^2+2*y*u*(sin(pi*x)+x/5); % подынтегральная функция

3.uc = x/10+y^2/50; % функция граничных условий

4. x1=0; x2=1; y1=0; y2=2; % координаты ограничивающего прямоугольника

5.fprintf('Подынтегральная функция: F=%s\n',char(F))

6.fprintf('Граничное условие на контуре: u=%s\n',char(uc))

7.fprintf('Область: %d<=x<=%d; %d<=y<=%d\n',x1,x2,y1,y2)

8.% ------------------------------------------------------------------------------------------

9.dFdu = diff(F,u); dFdp = diff(F,Dux); dFdq = diff(F,Duy);%поиск частных производных

10.% ------------------------------------------------------------------------------------------

11.% формируем полные производные ∂Fp/∂x и ∂Fq/∂y

12.d_dFdp_dx = diff(dFdp,x); d_dFdp_du = diff(dFdp,u); d_dFdp_dp = diff(dFdp,Dux);

13.d_dFdp_dq = diff(dFdp,Duy);

14.dFpdx = d_dFdp_dx + d_dFdp_du*Dux + d_dFdp_dp*D2ux2 + d_dFdp_dq*D2uxy

15.d_dFdq_dy = diff(dFdq,y); d_dFdq_du = diff(dFdq,u); d_dFdq_dp = diff(dFdq,Dux);

16.d_dFdq_dq = diff(dFdq,Duy);

17.dFqdy = d_dFdq_dy + d_dFdq_du*Duy + d_dFdq_dp*D2uxy + d_dFdq_dq*D2uy2

18.% ------------------------------------------------------------------------------------------

19.% Формируем уравнение Остроградского

20.Ost = dFdu-dFpdx-dFqdy

21.OstR = -subs(Ost,{u,D2ux2,D2uy2,D2uxy},{0,0,0,0}); % правая часть

22.OstL = Ost+OstR; % левая часть

23.deqOst = [ char(OstL) '=' char(OstR) ]; % уравнение

24.fprintf('Уравнение Остроградского:\n%s\n',deqOst)

25.% ------------------------------------------------------------------------------------------

26.% для решения используем специальный инструментарий – Partial Differential Equation %Toolbox (PDE), в котором используется метод конечных элементов (FEM). Для

%применения PDE нужно привести ДУ к виду: − div(C grad u)+ au = f	и дополнить его
%граничными условиями типа Дирихле: hu = r или Неймана: div (C grad	u ) + qu = g .

27.% Задаем геометрию (область решения), формируем треугольную FEM-сетку и рисуем %её.Печатаем количество узлов и элементов.

28.del=min(x2-x1,y2-y1)/20 % размер элемента

29.nx=round((x2-x1)/del); ny=round((y2-y1)/del);

30.[p,e,t]=poimesh('squareg',nx,ny); % формируем FEM-сетку

31.p(1,:)=(p(1,:)+1)/2*(x2-x1)+x1;

32.p(2,:)=(p(2,:)+1)/2*(y2-y1)+y1; % приводим к прямоугольной

33.np=size(p,2); nel=size(t,2); % число узлов и элементов

34.fprintf('Число узлов сетки разбиения np=%d\n',np)

35.fprintf('Число конечных элементов nel=%d\n',nel)

36.pdemesh(p,e,t) % рисуем сетку

37.da=daspect; da(1:2)=min(da(1:2)); % находим текущие масштабы осей и выравниваем их

38.daspect(da); % устанавливаем одинаковые масштабы

39.% ------------------------------------------------------------------------------------------

40.% Формируем *.m-файл для вычисления граничных условий Дирихле (boundary M-file), %который должен иметь структуру: [q,g,h,r]=pdebound(p,e,u,time). Формируем строки для %записи в файл и записываем их. Файл должен быть размещён в каком-либо каталоге, %доступном системе MATLAB – у нас это каталог С:\MATLAB701\work\

41.s{1}='function [q,g,h,r]=boundmem(p,e,u,time)'; % заголовок

42.s{2}='nb=size(e,2);'; % определили размерности

35

43.s{3}='q=zeros(1,nb); g=zeros(1,nb);'; % задали массивы условий Неймана

44.s{4}='h=ones(1,2*nb); r=zeros(1,2*nb);'; % задали массивы условий Дирихле

45.s{5}='xb=[p(1,e(1,:)),p(1,e(2,:))];'; % столбец координат x

46.s{6}='yb=[p(2,e(1,:)),p(2,e(2,:))];'; % столбец координат y

47.ucf=subs(uc,{x,y},{sym('xb'),sym('yb')}); % формула для подстановки

48.s{7}=['r=' vectorize(ucf) ';'];

49.disp('Текст файла граничных условий boundmem.m:')

50.fprintf('%s\n',s{:})

51.fid = fopen ('С:\MATLAB701\work\boundmem.m', 'w' );

52.fprintf(fid,'%s\n',s{:});

53.fclose(fid); % закрываем файл

54.% ------------------------------------------------------------------------------------------

55.% Подготовка коэффициентов (С, a) для решения ДУ методом конечных элементов. %Вычисляем правую часть уравнения Остроградского сначала аналитически, а потом

в%центрах тяжести конечных элементов.

56.a=eval(subs(OstL,{u,D2ux2,D2uxy,D2uy2},{1,0,0,0}))

57.c11=-eval(subs(OstL,{u,D2ux2,D2uxy,D2uy2},{0,1,0,0}));

58.c12=-eval(subs(OstL,{u,D2ux2,D2uxy,D2uy2},{0,0,1,0}))/2;

59.c22=-eval(subs(OstL,{u,D2ux2,D2uxy,D2uy2},{0,0,0,1}));

60.c=[c11;c12;c12;c22]

61.fp = subs(OstR,{x,y},{p(1,:),p(2,:)}); % f в узлах

62.f = (fp(t(1,:))+fp(t(2,:))+fp(t(3,:)))/3; % f в ц.т. конечных элементов

63.% ------------------------------------------------------------------------------------------

64.% Решаем уравнение и рисуем график решения

65.z = assempde('boundmem',p,e,t,c,a,f); % решили

66.pdeplot(p,e,t,'xydata',z,'zdata',z,'mesh','on','colorbar','off'); % рисуем

67.xlabel('x'); ylabel('y'); zlabel('u(x,y)'); % оси

68.v = axis; % границы осей

69.da = daspect; % масштаб осей

70.da(1:2) = min(da(1:2));

71.daspect(da) % выравняли масштаб осей

72.axis(v); % оставили границы

73.colormap(gray) % выбрали палитру

74.grid on; box on; % показали сетку и внешний контур

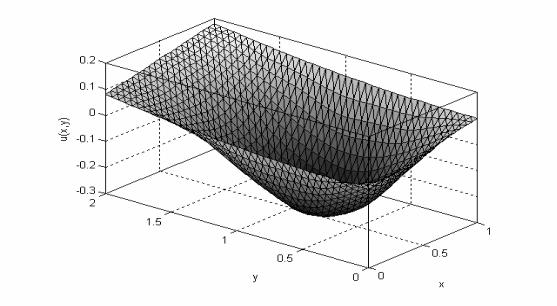
Ниже на рисунке приведен график поверхности, являющейся решением задачи.

36